目录

一.相关包及函数介绍

二.雅各比向量积

三.练习代码

---

一.相关包及函数介绍

autograd 包是 PyTorch 中所有神经网络的核心。首先让我们简要地介绍它，然后我们将会去训练我们的第一个神经网络。该 autograd 软件包为 Tensors 上的所有操作提供自动微分。它是一个由运行定义的框架，这意味着以代码运行方式定义你的后向传播，并且每次迭代都可以不同。我们从 tensor 和 gradients 来举一些例子。

1、TENSOR

torch.Tensor 是包的核心类。如果将其属性 .requires_grad 设置为 True，则会开始跟踪针对 tensor 的所有操作。完成计算后，您可以调用 .backward() 来自动计算所有梯度。该张量的梯度将累积到 .grad 属性中。

要停止 tensor 历史记录的跟踪，您可以调用 .detach()，它将其与计算历史记录分离，并防止将来的计算被跟踪。

要停止跟踪历史记录（和使用内存），您还可以将代码块使用 with torch.no_grad(): 包装起来。在评估模型时，这是特别有用，因为模型在训练阶段具有 requires_grad = True 的可训练参数有利于调参，但在评估阶段我们不需要梯度。

还有一个类对于 autograd 实现非常重要那就是 Function。Tensor 和 Function 互相连接并构建一个非循环图，它保存整个完整的计算过程的历史信息。每个张量都有一个 .grad_fn 属性保存着创建了张量的 Function 的引用，（如果用户自己创建张量，则grad_fn 是 None ）。

如果你想计算导数，你可以调用 Tensor.backward()。如果 Tensor 是标量（即它包含一个元素数据），则不需要指定任何参数backward()，但是如果它有更多元素，则需要指定一个gradient 参数来指定张量的形状。

可参考这篇博客：

PyTorch自动求导：Autograd

二.雅各比向量积

从数学上讲，autograd类只是一个雅可比向量积计算工具。简而言之，雅可比矩阵就是表示两个向量的所有可能偏导数的矩阵。它是一个向量相对于另一个向量的梯度。
注：在这个过程中，PyTorch从未显式地构造整个雅可比矩阵。直接计算JVP(雅可比向量积)通常更简单、更有效。
如果一个向量X = [x1, x2，…xn]用于计算其他向量f(X) = [f1, f2, …fn] 通过函数f，则雅可比矩阵(J)简单地包含了所有偏导数组合，如下所示:

 以上矩阵表示f(X)对X的梯度
设PyTorh支持梯度的tensor为
X = [x1, x2, …… xn]（假设这是某个机器学习模型的权重）
X经过一些运算得到向量Y
Y = f(X) = [y1, y2, …. ym]
然后用Y来计算标量损失l。假设向量v恰好是标量损失l对向量Y的梯度，如下所示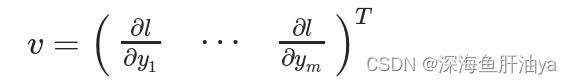

 向量v被称为grad_tensor，并作为参数传递给backward()函数
为了得到损失l对权值X的梯度，将雅可比矩阵J与向量v相乘

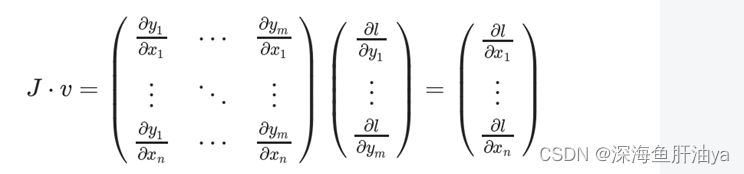
这种计算雅可比矩阵并将其与向量v相乘的方法使PyTorch能够轻松地提供外部梯度，即使是非标量输出。
个人理解：X是权重向量，Y是假设函数（Hypothesis function，比如交叉熵或线性函数），l则是整体的损失函数（比如均方误差）。
目的是要计算l关于X的梯度，但是可能直接计算不太方便或者代价大或者存在其他弊端。所以采用先计算Y关于X的梯度，再计算l关于Y的梯度，再利用结果计算l关于X的梯度，这样做应该是有某些好处。

三.练习代码

import torch

#创建一个张量，设置 requires_grad=True 来跟踪与它相关的计算
# x=torch.ones(2,2,requires_grad=True)
# print('x:',x)
# #
# # #针对张量做一个操作
# y = x + 2
# print('y:',y)
#
# #y 作为操作的结果被创建，所以它有 grad_fn
# # 每个张量都有一个 .grad_fn 属性保存着创建了张量的 Function 的引用，（如果用户自己创建张量，则grad_fn 是 None ）
# # print(y.grad_fn)
#
# #针对 y 做更多的操作：
# z = y * y * 3
# out = z.mean()
# print('z:',z, 'out:',out)

#.requires_grad_( ... ) 会改变张量的 requires_grad 标记。输入的标记默认为 False ，如果没有提供相应的参数。
#2行2列的张量
# a = torch.randn(2, 2)
# a = ((a * 3) / (a - 1))
# print(a.requires_grad)
# a.requires_grad_(True)
# print(a.requires_grad)
# b = (a * a).sum()
# print(b.grad_fn)

'''
梯度：
我们现在后向传播，因为输出包含了一个标量，out.backward() 等同于out.backward(torch.tensor(1.))。
'''
# 调用 Tensor.backward()来计算导数
# out.backward()
# # 打印梯度 d(out)/dx
# print(x.grad)

# 现在让我们看一个雅可比向量积的例子：
#1行3列
x = torch.randn(3, requires_grad=True)
y = x * 2
'''
data.norm()对张量y每个元素进行平方，然后对它们求和，最后取平方根。 这些操作计算就是所谓的L2范数或欧几里德范数 。
L1范数是指向量中各个元素绝对值之和。
'''
while y.data.norm() < 1000:
    y = y * 2
# print(y)
'''
现在在这种情况下，y不再是一个标量(只有一个元素才叫做标量)。torch.autograd 不能够直接计算整个雅可比矩阵，
但是如果我们只想要雅可比向量积，只需要简单的传递向量给 backward 作为参数。 
'''
v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)
print(x.grad)

'''
你可以通过将代码包裹在 with torch.no_grad()，来停止对从跟踪历史中 的 .requires_grad=True 的张量自动求导。 
'''
# print(x.requires_grad)
# print((x ** 2).requires_grad)
# with torch.no_grad():
#     print((x ** 2).requires_grad)