1 数据结构的相关概念

1.1 为什么要学习数据结构

数据结构与之前的设计模式具有相似的特点，均是思想层面的东西，与具体的语言无关，因此使用其他的语言去实现这些思想也都是可以的。
设计模式是在教我们如何编写代码，让代码具有可扩展性，这个是编码层次的，数据结构呢？有以下一个例子
在C语言中是没有数组这个数据结构的，那么如何去实现10个数的排序呢？这就需要我们自己定义10个变量，然后将10个变量互相比较，重复劳动，但是使用数组之后，问题就会变得简单，只需要通过数组下标就可以，从而提高了程序的编写效率。
再比如说，在已经有数组的情况下，为什么还是需要学习链表这种数据结构？
数组是连续内存空间，一旦定义了不能改变，适应性差，但是链表你有多少数据，就可以创建多少个节点，比如说数据，你删除中间位置一个元素，会引起后边数据的移动，但是链表就不会，在有些情况下，使用链表会增加程序的效率。

从以上可以看出数据结构的概念，数据结构就是帮助我们解决如何组织和存储数据的方式
数据结构主要研究：非数值计算问题的程序中的操作对象以及他们之间的关系，不是研究复杂的算法数据结构是计算机存储，组织数据的方式。

1.2 数据结构中的基本概念

在这里插入图片描述

2 算法

2.1 算法的概念

为什么学习数据结构还需要了解算法？
比如说：将10个学生信息保存到一个链表中，但是不能只是简单的将数据存储进去，还需要根据一定的业务需求，比如按照成绩大小排序并显示，比如计算这些学生的平均分等，这些才是我们最终要解决的问题，既然要解决问题，那么就需要一些算法，比如排序算法，比如计算平均分的算法。所以数据结构和算法是互相配合完成工作。
算法是特定问题求解步骤的描述，在计算机中表现为指令的有序排列，算法是独立存在的一种解决问题的方法和思想。
对于算法而言，语言并不重要，重要的是思想。

2.2 算法和数据结构的区别

数据结构只是静态的描述了数据元素之间的关系，高效的程序需要在数据结构的基础上设计和选择算法。

算法是为了解决实际问题而设计的
数据结构是算法需要处理的问题载体
数据结构与算法相辅相成

2.3 算法特性

在这里插入图片描述
问题：针对某一具体的问题，针对这一问题算法是唯一的吗？
答案是不唯一的

比如说：求1到100的和
算法1：程序申请堆空间，返回空间内存首地址–>将数据放到内存中–>对内存中数据进行累计得到1到n的和
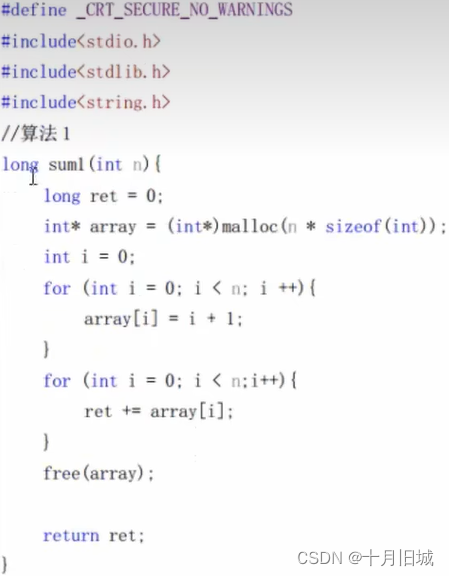
在这里插入图片描述
算法2：直接采用for循环来进行计算

算法3：通过数学公式来进行计算

同样的一个问题，有三种不同的算法，这三种算法都可以解决同样的问题，那么如何进行选择？需要有个方法来衡量算法的效率

2.4 算法效率的度量

2.4.1 事后统计法

此种方法仅做了解，主要是通过设计好的测试程序和数据，利用计算机的计时器对不同算法编制的程序的运行时间进行比较，从而确定算法效率的高低

统计方法
比较不同算法对同一组输入数据的运行处理时间
缺陷
-为了获得不同算法的运行时间必须编写相应程序；
-运行时间严重依赖硬件以及运行时的环境因素；
-算法的测试数据的选取相当困难
总结
事后统计法虽然直观，但是实施困难且缺陷多

2.4.2 事前分析估算

在计算机程序编制前，依据统计方法对算法进行估算。根据最终编译成的具体的计算机指令，每条指令运行时间固定，通过推导的方式得到算法的复杂度。

统计方法
-依据统计的方法对算法效率进行估算
影响算法效率的主要因素：
-算法采用的策略和方法；
-问题的输入规模；
-编译器所产生的代码；
-计算机执行速度
算法推导的理论基础
-算法最终编译成具体的计算机指令；
-每一个指令，在具体的计算机上运行速度固定；
-通过具体的步骤，就可以推导出算法的复杂度（如下表）

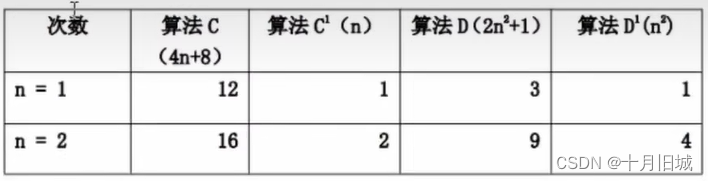
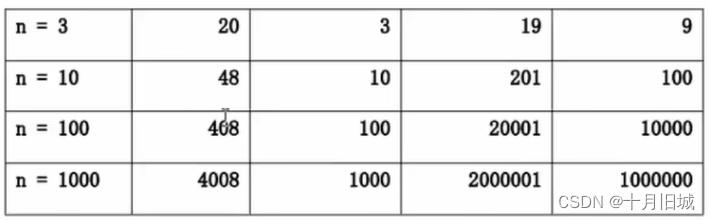
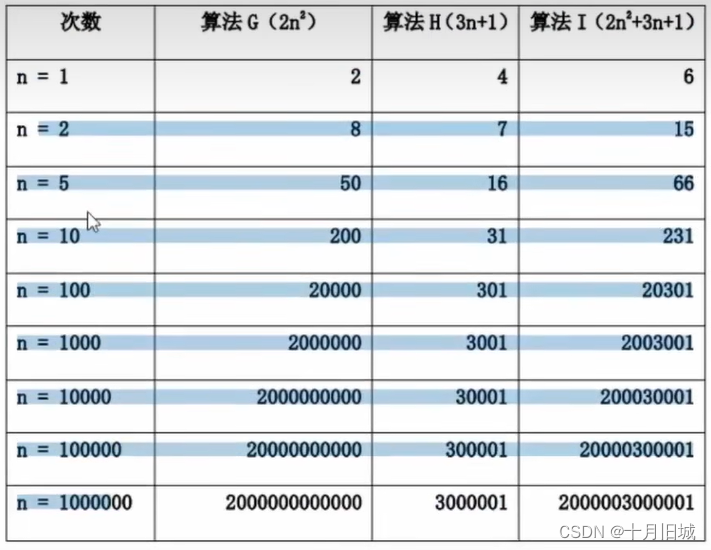
在这里插入图片描述

怎么判断一个算法的效率?(规则如下)
-判断一个算法的效率时，往往只需要关注操作数量的最高次项，其他次要项和常数项可以忽略（例如上面的操作次数，当n不同时，每一个算法的具体执行次数是不同的，只看20000000000最高次项的值）；
-在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度（最worst情况下的）；
-只有常数项记作1；
-操作数量的估算可以作为时间复杂度的估算

2.4.3 大O表示法

本课程重点讲解的方法

算法的时间复杂度
-常见的时间复杂度

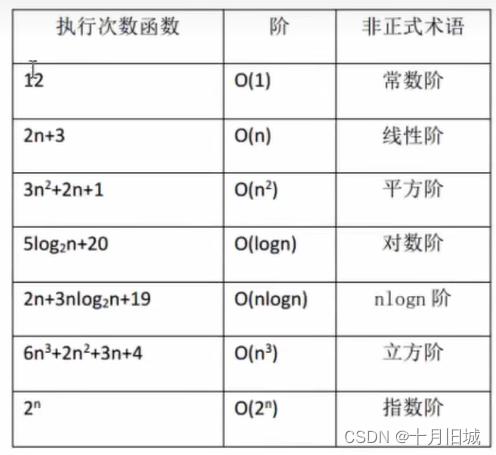
常见时间复杂度之间的关系

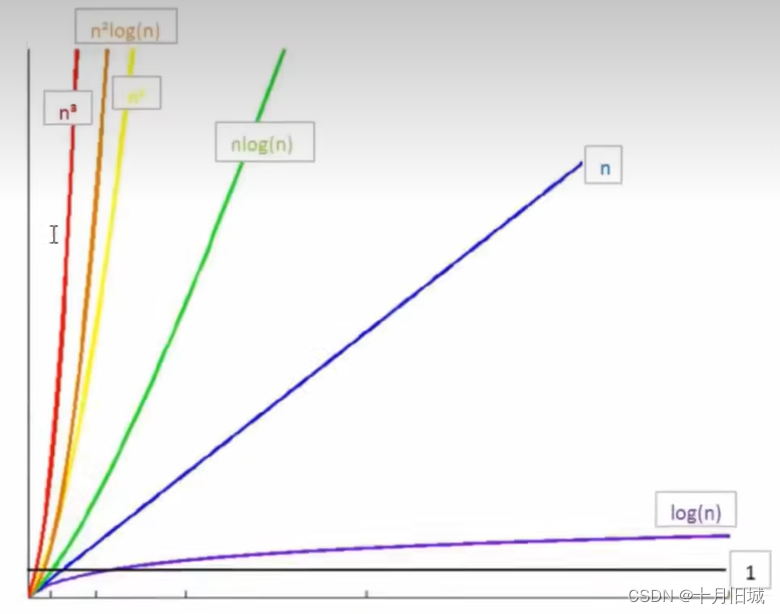
总结：
只关注最高次项
时间复杂度是指最坏时间复杂度
只有常数项记作1

-算法的空间复杂度
算法的空间复杂度并不是计算所有算法所占的空间，而是使用的辅助空间的大小

2.4.3.1采用大O表示法表示算法的时间复杂度的相关练习

算法1：
在这里插入图片描述
算法1的程序中代码总共会执行3步，次数为常数项，用大O表示法为：O(1)

算法2：
在这里插入图片描述
算法2的程序中代码总共会执行12步，次数为常数项，用大O表示法为：O(1)

算法3：
在这里插入图片描述
算法3的执行次数与n相关，使用O(n)进行表示

算法4：
在这里插入图片描述
算法4中count22*…，以2的n次方接近n，也就是2x=n，x=log2n，利用大O表示法表示为O(logN)
logaN=logcN/logca，如果算法复杂度的最高次项的乘数，如果不是1的话就直接舍去，对于算法复杂度logaN来说，其最高次项就是logcN*1/logca，其乘数1/logca不是个1，可以直接省掉，也就变为logcN，c可以是任意值，因此表示为logN。