一、分类
1、自顶向下
顾名思义,就是从某一个节点(不一定是根节点),从上向下寻找路径,到某一个节点(不一定是叶节点)结束,具体题目如下:而继续细分的话还可以分成一般路径与给定和的路径
- 二叉树的所有路径
- 面试题 04.12. 求和路径
-
- 路径总和
-
- 路径总和 II
- 437 路径总和 III
- 988 从叶结点开始的最小字符串
2、非自顶向下:
就是从任意节点到任意节点的路径,不需要自顶向下
124. 二叉树中的最大路径和
125. 最长同值路径
126. 二叉树的直径
二、关于递归
- 回溯和递归式一一对应的。回溯的目的是path 不能一直加入节点,它还要删节点,然后才能加入新的节点。
- 递归函数的返回值问题
- 如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值。(113.路径总和ii)
- 如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值。 (236. 二叉树的最近公共祖先 )
- 如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回。(112.路径总和)
三、解题模板
这类题通常用深度优先搜索(DFS)和广度优先搜索(BFS)解决。所以掌握二叉树的遍历思想很重要。
1、自顶而下
一般路径
// 定义一个数组,用于存储遍历二叉树时走过的所有路径
let res = []
// 遍历二叉树,一般而言,就是使用DFS或者是BFS
// 遍历的时候,每进入一个分支,需要将当前节点的值放入path中,path代表是每条路径。
// 当一个分支结束也就是单层递归结束的时候,将path放入最后的res
var dfs = function(root,path){
if(!root) return // 节点为空,直接返回
// 处理根节点
path.push(root.val)
//单个分支结束递归条件,节点root为叶子节点
if(!root.left && !root.right){
res.push(path)
return
}
// 节点root为非叶节点,检查左右节点继续遍历
// 此时会一直向左走,即先遍历完左子树
if(root.left){
dfs(root.left,path)
path.pop() // 回溯
}
// 左子树结束,此时还在倒数第二节点的递归内,所以此时是回溯了
if(root.right){
dfs(root.right,path)
path.pop() // 回溯
}
}
dfs(root,[])
// 返回最后的结果数组,即所有的路径
return res
给定和的路径
// 定义一个数组,用于存储遍历二叉树时满足条件的路径
let res = []
// 遍历二叉树,一般而言,就是使用DFS或者是BFS
// 遍历的时候,每进入一个分支,需要将当前节点的值放入path中,path代表是每条路径。并且需要将目标值sum-节点当前值。
// 当一个分支结束也就是单层递归结束的时候,检查sum是否为0
var dfs = function(root,sum,path){
if(!root) return // 节点为空,直接返回
// 每遍历到一个节点的逻辑
path.push(root.val) // 做出选择
sum -= root.val
//单个分支结束递归条件:节点root为叶子节点
// 检查到满足条件的路径:sum此时为0
if(!root.left && !root.right && sum == 0){
res.push(path)
return
}
// 节点root为非叶节点,继续遍历左右子树
if(root.left){
dfs(root.left,sum,path)
path.pop() // 回溯
}
if(root.right){
dfs(root.right,sum,path)
path.pop() // 回溯
}
}
dfs(root,sum,path)
// 返回最后的结果数组
return res
2、非自顶而下
思想:设计一个辅助函数maxpath,调用自身求出以一个节点为根节点的左侧最长路径left和右侧最长路径right,那么经过该节点的最长路径就是left+right。每次不断更新全局变量即可。
注意:
- left,right代表的含义要根据题目所求设置,比如最长路径、最大路径和等等
let res=0;
// 递归函数需要返回值
var maxPath = function(root) //以root为路径起始点的最长路径
{
// 单层递归结束条件
if (!root) return 0;
// 单层逻辑
int left=maxPath(root.left);
int right=maxPath(root.right);
res = max(res, left + right + root.val); //更新全局变量
// 单层递归逻辑的返回值
return max(left, right); //返回左右路径较长者
}
maxPath(root)
return res
三、题目
257. 二叉树的所有路径
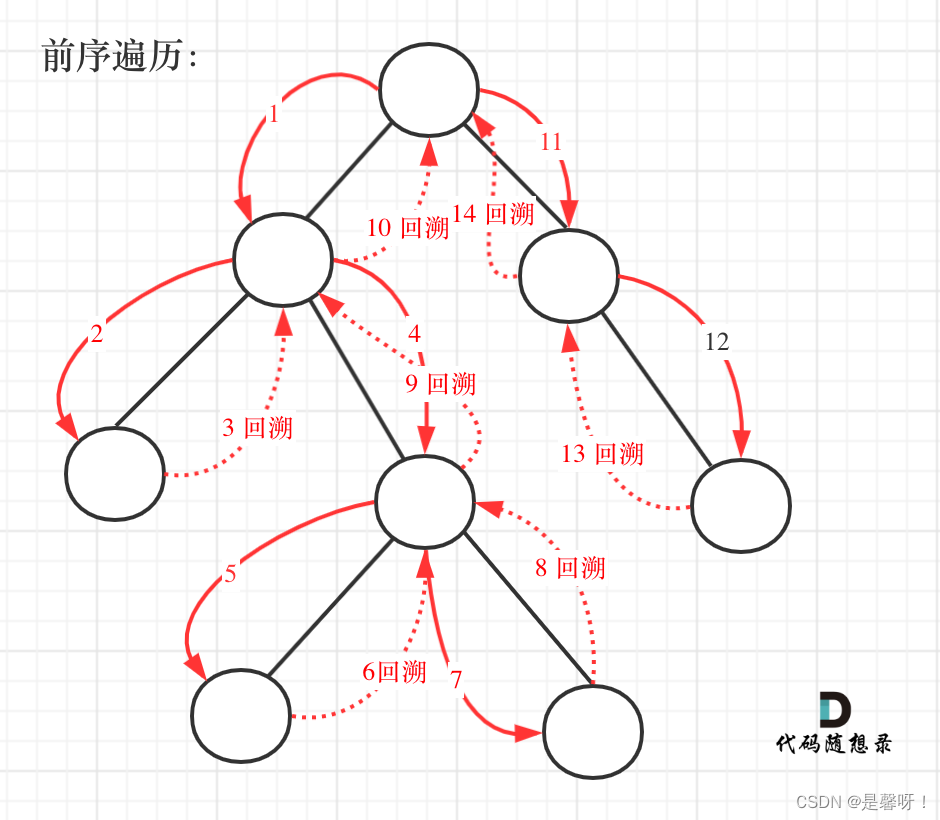
使用模板1。递归函数不需要返回值。
var binaryTreePaths = function(root) {
// res是最后的结果数组,不参与遍历
let res = []
// 1. 确定递归函数 函数参数。这里的递归函数不需要返回值。
var dfs = function (root,path){
if(!root) return
path += String(root.val)
// 2. 确定终止条件,叶子节点,将单分支路径path放入res,并且结束单分支路径
if(!root.left && !root.right){
res.push(path)
return // 单层递归结束
}
// 3. 确定单层递归逻辑,非叶节点
if(root.left){
dfs(root.left,path+ '->')
}
if(root.right){
dfs(root.right,path+ '->')
}
}
dfs(root,"")
return res
};
其实这个题目是运行了回溯的,回溯就隐藏在 dfs(root.right,path+ ‘->’);中的 path + “->”。上面的代码实际上是下面的代码。
当最左边的分支结束,即叶子节点7递归结束。回到了11节点的递归中,此时检查11的右节点是否存在。
if (cur->left) {
path += "->";
traversal(cur->left, path, result); // 左
path.pop_back(); // 回溯 '>'
path.pop_back(); // 回溯 '-'
}
if (cur->right) {
path += "->";
traversal(cur->right, path, result); // 右
path.pop_back(); // 回溯 '>'
path.pop_back(); // 回溯 '-'
}
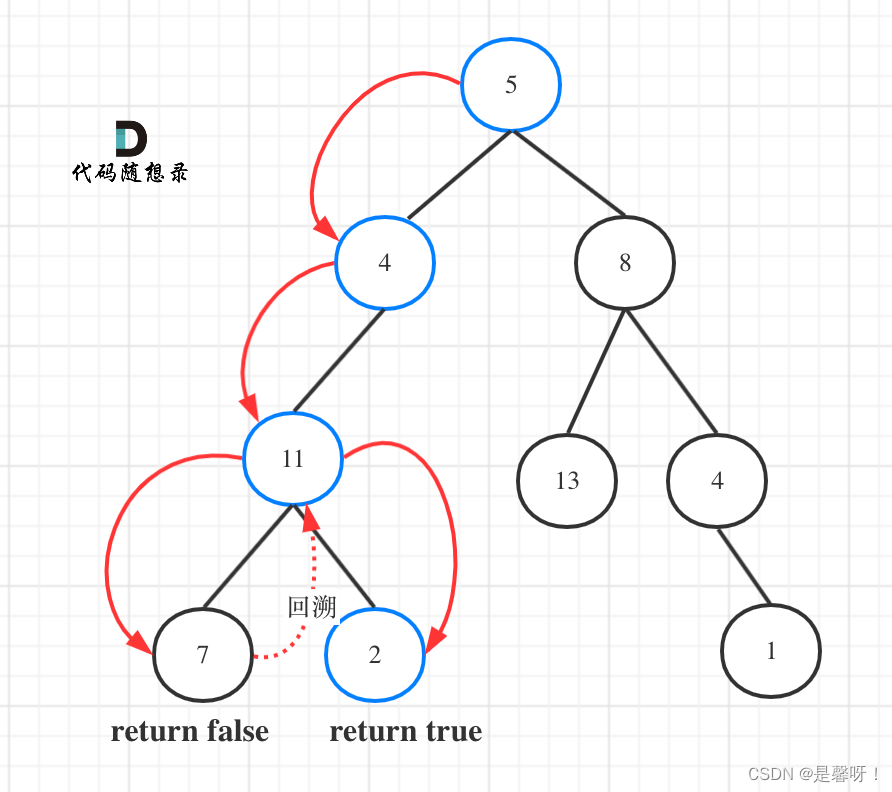
112. 路径总和
使用模板2,这个题目不是返回路径,而是判断是否存在。注意这个递归函数是需要返回值的,即遇到合适的路径立刻返回,不需要遍历整棵树。
var hasPathSum = function(root, targetSum) {
// 1、不需要返回值
var dfs = function(root,reSum){
// 2、终止条件
// 叶子节点,且和为sum
if(!root.left && !root.right && reSum== 0){
return true
}
// 叶子节点,和不为sum
if(!root.left && !root.right && reSum!= 0){
return false
}
// 3、单层递归逻辑,需要返回值
// 遇到叶子节点返回true,则直接返回true
if(root.left && hasPathSum(root.left,reSum-root.left.val)){
return true
}
if(root.right && hasPathSum(root.right,reSum-root.right.val)){
return true
}
// 其他情况就是fasle
return false
}
if(!root) return false
// 需要返回值
return dfs(root,targetSum-root.val)
};
以上代码中是包含着回溯的,没有回溯,如何后撤重新找另一条路径呢。
回溯隐藏在(root.right,reSum-root.right.val)这里, 因为把reSum-root.right.val直接作为参数传进去,函数结束,reSum的数值没有改变。
if (cur->left) { // 左
count -= cur->left->val; // 递归,处理节点;
if (traversal(cur->left, count)) return true;
count += cur->left->val; // 回溯,撤销处理结果
}
if (cur->right) { // 右
count -= cur->right->val;
if (traversal(cur->right, count)) return true;
count += cur->right->val;
}
return false;
113. 路径总和 II
使用模板2
var pathSum = function(root, targetSum) {
let res = [],path = [];
// 1、递归函数,不需要返回值
var dfs = function(root,reSum,path){
// 2、分支递归结束条件 叶子节点
if(!root.left && !root.right && reSum== 0){
// 深拷贝
res.push([...path])
return // 结束单分支
}
if(!root.left && !root.right && reSum!= 0) return;
// 非叶
if(root.left){
// 存值
path.push(root.left.val)
dfs(root.left,reSum-root.left.val,path) // 这里也有回溯的思想,参考上一题
// 一直向左之后,需要回溯,进入下一个分支
path.pop() // 回溯,将存入的值弹出
}
if(root.right){
path.push(root.right.val)
dfs(root.right,reSum-root.right.val,path)
path.pop()
}
// 其他
return;
}
if(!root) return res;
// 把根节点提前放入路径
dfs(root,targetSum-root.val,[root.val])
return res
};
实际上的两处回溯:
if (cur->left) { // 左 (空节点不遍历)
path.push_back(cur->left->val);
count -= cur->left->val;
traversal(cur->left, count); // 递归
count += cur->left->val; // 回溯
path.pop_back(); // 回溯
}
if (cur->right) { // 右 (空节点不遍历)
path.push_back(cur->right->val);
count -= cur->right->val;
traversal(cur->right, count); // 递归
count += cur->right->val; // 回溯
path.pop_back(); // 回溯
}
543. 二叉树的直径
使用模板3,求出的是路径的长度最大值
整个二叉树路径最长 = 左子树最长+右子树最长,所以使用递归的思想。
var diameterOfBinaryTree = function(root) {
// res统计路径
let res = 0
// 整个二叉树路径最长 = 左子树最长+右子树最长
var maxDepth = function(root){
// 递归结束条件
if(!root) return 0
// 单层递归逻辑
// 左最长
let left = maxDepth(root.left)
// 右最长
let right = maxDepth(root.right)
// 更新全局变量res
res = Math.max(left+right,res)
// 返回值
return Math.max(left,right)+1
}
maxDepth(root)
return res
};
124. 二叉树中的最大路径和
使用模板3,求出的是路径上节点的和的最大值.
var maxPathSum = function(root) {
// 最大路径和,res为负无穷,因为节点值可能为负数
// 全局变量res的初值设置是0还是-Infinity要看题目节点是否存在负值,如果存在就用-Infinity,否则就是0
let res = -Infinity
// 递归函数
var dfs = function(root){
// 单层递归结束条件
if(!root) return 0
// 左右子树的和最大值,节点值可能为负数
let left = Math.max(dfs(root.left),0)
let right = Math.max(dfs(root.right),0)
// 更新res
res = Math.max(left+right+root.val,res)
// 单层逻辑返回值
return Math.max(left,right)+root.val
}
dfs(root)
return res
};



![[附源码]java毕业设计疫情背景下社区公共卫生服务系统](https://img-blog.csdnimg.cn/15054854ad2540da850cb2a800f4eebb.png)