写在前面

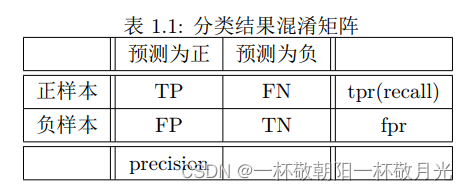
用 True（T）和 False（F）分别表示预测是正确还是错误。
用 positive（P）和 negative（N）分别表示预测为正例和预测为负例。

$TPR = R = \frac{TP}{TP + FN}$ ， [TP] / [正样本数目]

$FPR = \frac{FP}{FP+TN}$ ，[FP]/[负样本数目]

$P = \frac{TP}{TP+FP}$ , [TP] / [预测为正的数目]

$accuracy = \frac{TP+TN}{FP+FN}$ , [预测正确的数目] / [预测错误的数目]

$F-measure = \frac{2}{1/P + 1/R}$

分类任务有两类输出：一类是直接输出离散值，即直接预测类别；一类是输出连续值，可以理解为属于正例的概率。

ROC space

ROC曲线是用来权衡收益（true positive）和损失（false positive）的。

先看直接预测类别的

那些直接预测类别的分类器，仅能产生出一对(fpr,tpr)，具体的表现在ROC的图上就是一个单独的点。我们知道ROC曲线可以通过卡阈值来得到一堆(fpr,tpr)的pair对，它们的连线就是我们常见的ROC曲线。但是直接预测标签的，只能输出离散值如0/1，这就不能卡不同阈值来得到一堆(fpr,tpr)的pair对了。

一些特殊的点的解释：

(0,0)，表示 tpr 和 fpr 均为0，即 TP 和 FP 均为0，也即分类器从不会将样本判为正例，所有的预测类别均是负例。(1,1)表示 tpr 和 fpr 均为1，即 TP 和正样本数目相等，即所有的正例均预测为正，FP 于负样本数目相等，即所有的负例均预测为正，也即分类器给出全是正例的判定。(0,1)表示完美的分类器。

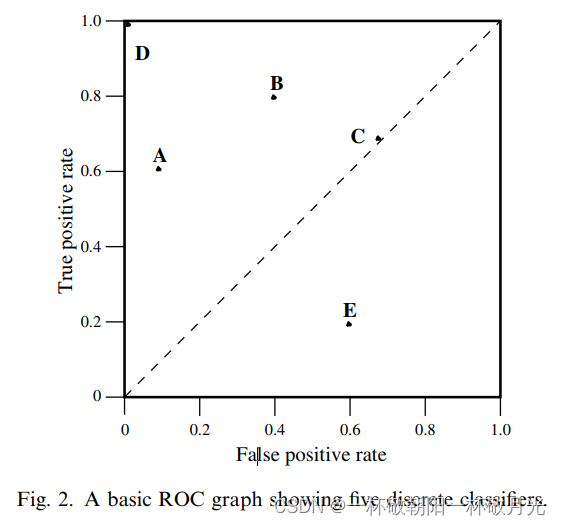
若在ROC曲线的左上半且临近X轴，表明该分类器比较保守，它们仅在置信度很高的情况下判为正例，所以很少产生FP（将负样本预测为正），但是它们的TP比例也很少。例如相对于B，A比较保守，具体表现为A的横纵坐标均小于B的横纵坐标。现实世界的许多场景被大量的负例支配，因此ROC图最左侧的性能变得更加重要。

关于随机

对角线 y=x 表示随机猜测类别的策略。例如若一个分类器以50%的概率随机预测为正类，那么它可以预期得到一半的正类和一半的负类；这产生ROC空间中的点(0.5,0.5)。如果它在90%的概率内预测为正类，那么它可以预期得到90%的阳性正确率，但其假阳性率也将增加到90%，在ROC空间中产生(0.9,0.9)，与样本中正负比例不相干，随机意味着一个样本以p的概率预测为正，也即正样本是以p的概率预测为正，这就是 tpr ，负样本以p的概率预测为正，这就是fpr，可见 tpr=fpr=p 。

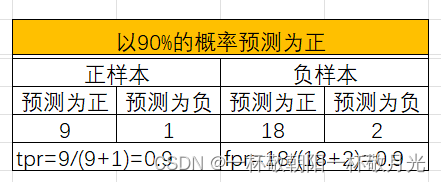
如果我们否定一个分类器，也就是说，在每一个实例上反转它的分类决策，那么它的真阳性分类就变成假阴性错误，而假阳性就变成真阴性。因此，任何在右下三角中产生点的分类器都可以被否定以在左上三角中产生一个点。Therefore, any classifier that produces a point in the lower right triangle can be negated to produce a point in the upper left triangle。例如反转后，E就得到B。这种可以反转的性质也是由于分母分别是正样本数目和负样本数目，与预测类别无关。举例如下，可见反转前后两个tpr之和为1，两个fpr之和也为1，原本在右下区域的【tpr < fpr，即 1-tpr > 1-fpr】，反转后就是tpr>fpr，在左上区域。

反转前
	预测为正	预测为负
正样本	a	b
负样本	c	d

反转后
	预测为正	预测为负
正样本	b	a
负样本	d	c

ROC曲线

这里指预测是连续值，并不一定是严格意义上代表概率。由于样本数目有限ROC曲线是阶跃的形式，随着样本数目增多，ROC曲线会变得光滑。PR曲线并不是一直降的（中间可能有反复）；ROC曲线是一直上升的（或者说不会存在下降的地方）。

将预测值逆序排序，先卡一个很大的正数做阈值，这时候分类器不会给出预测正的决策，即图上的点(0,0)，随着我们降低阈值到最大的输出值（对应图上的0.9）,这时候只有一个样本被判定为正样本，对应图上的(0,0.1)。直至最后我们将阈值降到最小输出值（图上的0.1），这时候所有样本均被判为正，对应图上的(1,1)。貌似在保守区ROC曲线上来看表现的更好，ROC曲线在(0.1,0.5)，对应的阈值是0.54（而不是0.5，This is equivalent to saying that the classifier is better at identifying likely positives than at identifying likely negatives），处达到最大accuracy（70%）。