该算法是托尼·霍尔在1960年提出。

算法思想：从集合中随机取一个数作为支点，然后将比它大的数放在一个集合里，比它小的数放在另一个集合中，然后再递归下去，最后便可求得有序的数组。

QuickSort(A)
1: S− = {}; S+ = {};
2: Choose a pivot A[j] uniformly at random;
3: for i = 0 to n − 1 do
4: Put A[i] in S− if A[i] < A[j];
5: Put A[i] in S+ if A[i] ≥ A[j];
6: end for
7: QuickSort(S+);
8: QuickSort(S−);
9: Output S−, then A[j], then S+;

其算法的精髓在于这个支点是随机获取的，这让这个算法变得十分的高效，下面我们来分析它的时间复杂度。
最坏的情况：选了最小的或者最大的数最为每次的支点。

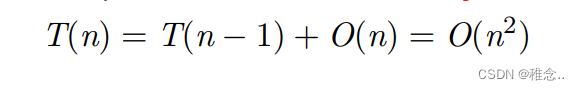
最好的情况：每次都选的中间的数作为它的支点。

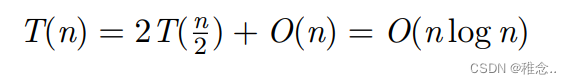
大多数的情况：选的不是最好的一个，选的是中间附近的一个数。

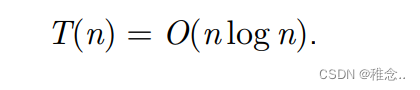
最好和坏情况下的时间复杂度我们可以很好的计算出来，下面我们来证明一下大多数情况下的时间复杂度：时间复杂度其实就是在计算各个元素之间的比较次数，首先我们可以看出，每两个元素之间最多会比较一次。所以我们可以去求元素之间比较的次数的期望E[X]，他就可以代表大多数情况下的时间复杂度

Pr(A˜[i] is compared with A˜[j])就是两个元素进行比较的可能性，为2/(j-i+1).

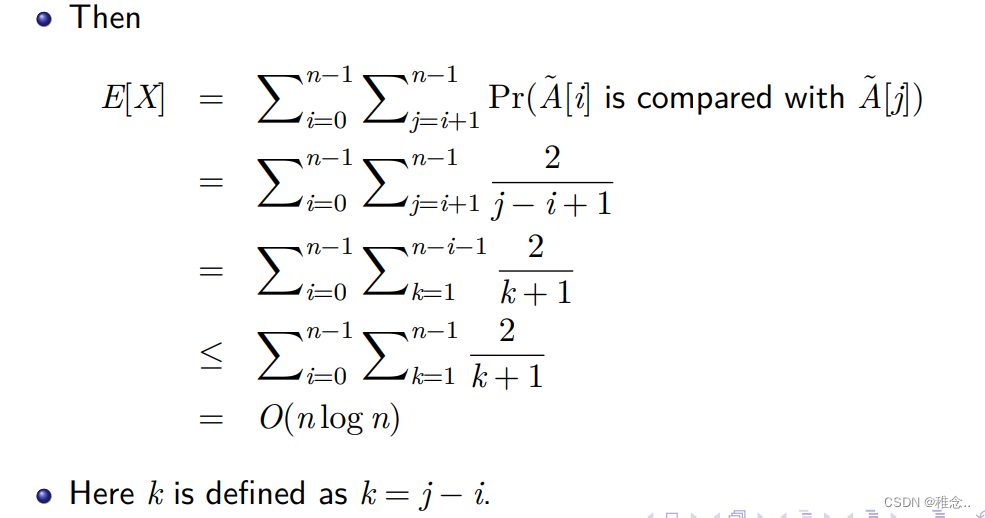
找一个数很难，但如果是找一个满足一定范围的数可能会简单很多，所以我们不一定非要找中间的数作为支点，也可以找中间附近的数作为支点。

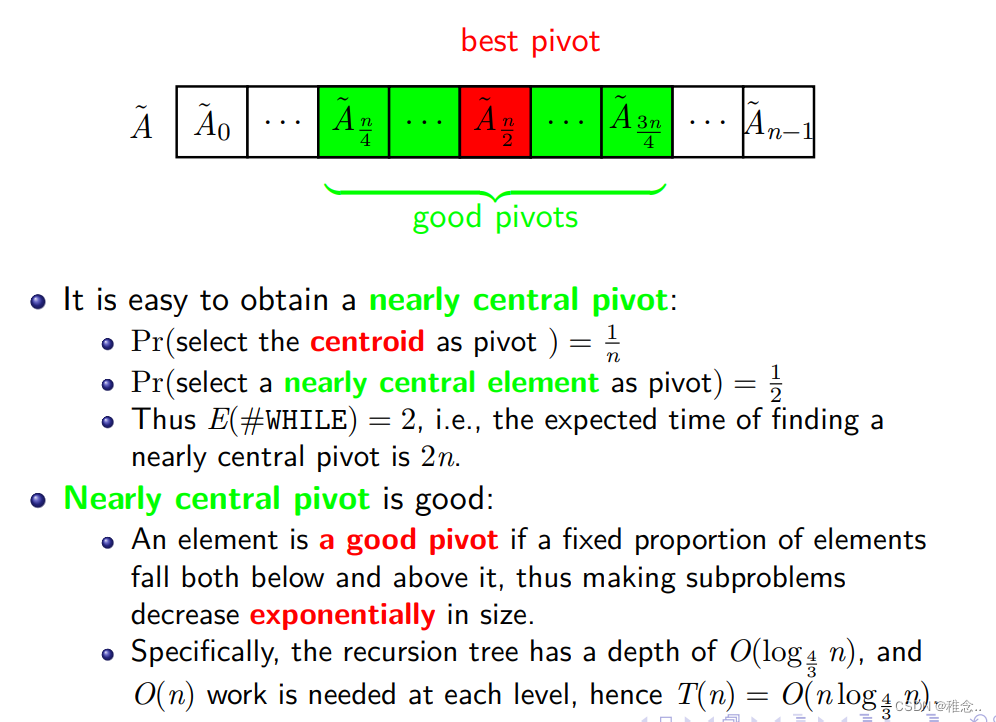
从上面的图我们可以看出，其中有一半的数都可以作为支点，且时间复杂度也很低，这样这个问题的难度就大大降低了。由之前1/n的概率减小到1/2。其实这个范围是不确定的，我们也可以选一个其它的范围，然后计算它的时间复杂度，也会有满足要求的范围。

ModifiedQuickSort(A)
1: while TRUE do
2: Choose a pivot A[j] uniformly at random;
3: S− = {}; S+ = {};
4: for i = 0 to n − 1 do
5: Put A[i] in S− if A[i] < A[j];
6: Put A[i] in S+ if A[i] ≥ A[j];
7: end for
8: if ∥S+∥ ≥ n
4
and ∥S−∥ ≥ n
4
then
9: break; //A fixed proportion of elements fall both below and
above the pivot;
10: end if
11: end while
12: ModifiedQuickSort(S+);
13: ModifiedQuickSort(S−);
14: Output S−, then A[j], and finally S+;

归并排序与快速排序的比较

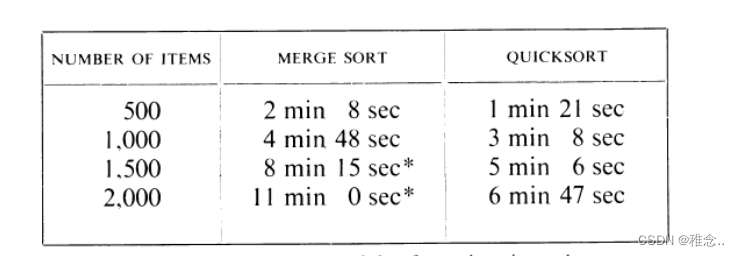
所以在大多数情况下还是快速排序比较的快，但它并不能保证每一次都会很快，如果有人特意设置一个陷阱，那么你的快速排序时间复杂度就可能为O(n^2)。