目录
树的定义
二叉树的定义
二叉树的性质
满二叉树
完全二叉树
二叉树的存储结构
顺序存储结构
链式存储结构
遍历二叉树(递归)
二叉树的层次遍历
先序创建二叉树
复制二叉树
销毁二叉树
写在最后
树的定义
树是n个结点的有限集(n>=0)
若n=0,则称为空树
若n>0,则满足如下条件:
- 有且仅有一个特定的结点,称为根
- 其余结点可分为m个互不相交的有限集T1,T2,T3...Tm(m>=0),其中每个集合本身又是一棵树,称为根的子树
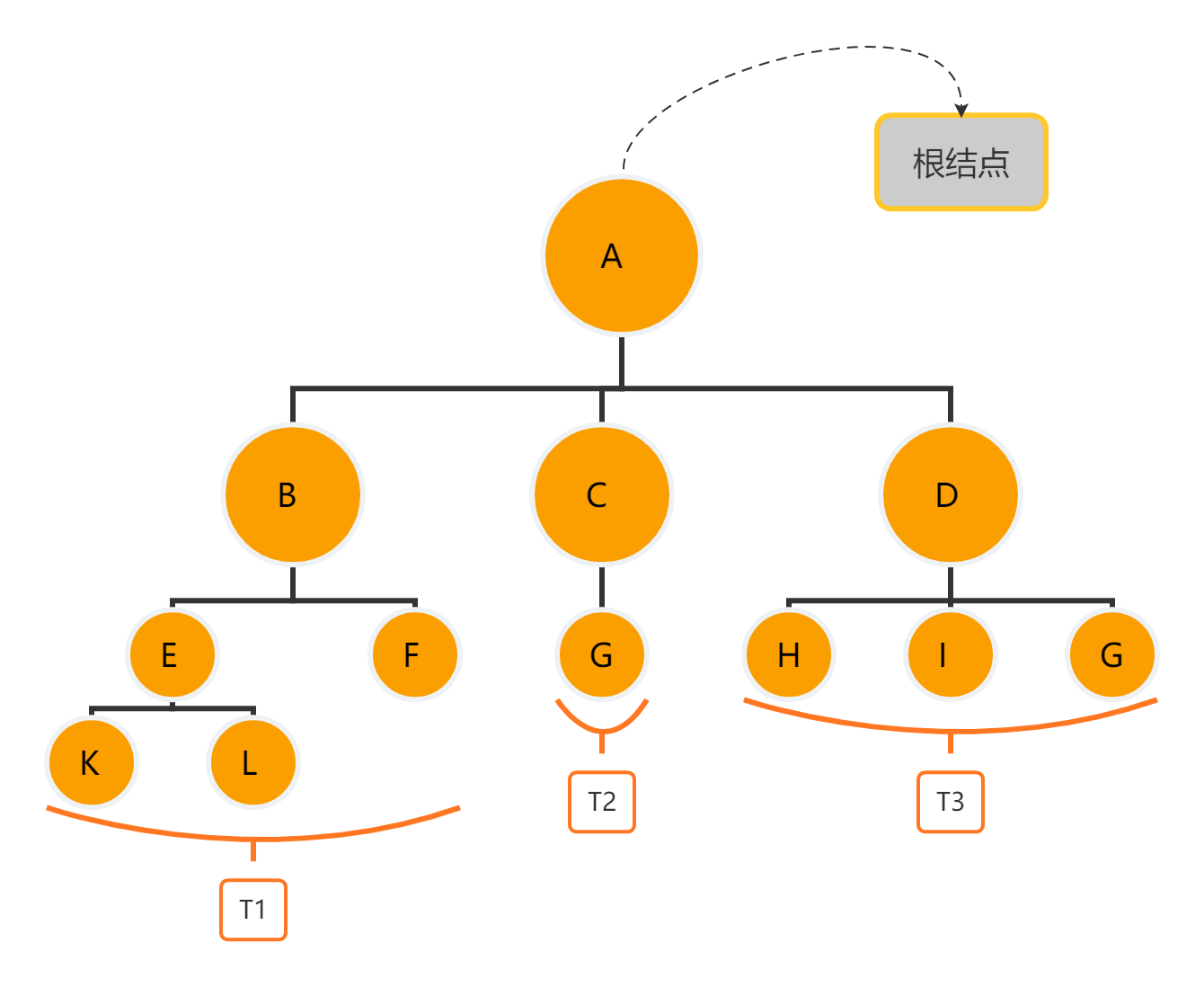
| 根结点 | 非空树中没有前驱结点的结点,例如A |
| 结点的度 | 结点拥有的子树的个数,例如:A的度为3,B的度为2,H的度为0 |
| 叶子/终端结点 | 结点的度等于0,例如:K,L,H |
| 分支/非终端结点 | 结点的度不等于0,例如:D |
| 树的度 | 树内个结点的最大值,例如图示,树的度为3 |
| 树的深度 | 把上图的结点每一行记为一层,树的深度就是层数的最大值,在本例中就是4 |
二叉树的定义
二叉树是n(n>=0)个结点的有限集,不是树的特殊情况,两者是两个概念
- 当n等于0时是空集;
- 当n不等于0时,由一个根结点以及两个互不相交的左子树、右子树组成。
如果二叉树有三个结点,则用二叉树和普通树分别表示为:


二叉树的性质
- i 层中最多有
个结点,至少有 1 个结点。
- 深度为K的二叉树至多有
个结点,至少有 k 个结点。
- 对于一棵二叉树,叶子树为
,度为2 的结点数为
,那么
满二叉树
性质:
- 每一层的结点都是满的;
- 叶子结点均在最底层;
- 每个结点位置均有元素;
- 编号规则:自上而下,自左而右;

完全二叉树
具有n个结点的完全二叉树的深度为[]+1( [x]表示不大于x的最大整数),在一个满二叉树中,从最后一个结点开始,连续去掉任意个结点,即是一个完全二叉树。
性质:
如果对一棵有n个结点的完全二叉树,则对任一结点i(1<=i<=n)有:
- 双亲结点:如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则双亲结点为 [
];(向下取整)
- 左孩子:如果2i>n,则结点i为叶子结点;否则,其左孩子结点为2i;
- 右孩子:如果2i+1>n,则结点i无右孩子;否则,其右孩子是结点2i+1;
二叉树的存储结构

顺序存储结构
缺点:会出现最坏的情况,深度为k的且只有k个结点的单只树需要长度为的一维数组,空间浪费严重,比较适合满二叉树,和完全二叉树的情况
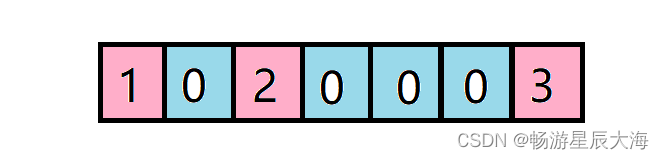

链式存储结构
头文件
#include "Queue.h"
#include "Stack.h"
#include "define.h"
#ifndef __BINARYTREE_H
#define __BINARYTREE_H
typedef char BitreeElemType;
typedef struct __BiNode
{
BitreeElemType data;
__BiNode *lchild, *rchild;
}BiNode, *BiTree;
void InOrder(BiTree T);
void PreOrder(BiTree T);
void PostOrder(BiTree T);
void LevelOrer(BiTree T);
void Copy(BiTree *Tnew, const BiTree T);
void Destroy(BiTree *root);
#endif二叉链表
typedef char ElemType;
typedef struct BiNode
{
ElemType data;
struct BiNode *lchild, *rchild;//左孩子,右孩子指针
} BiNode, *BiTree;遍历二叉树(递归)
| 先序遍历 | 中序遍历 | 后序遍历 |
| 若二叉树为空,则空操作 | ||
| 访问根节点; 先序遍历左子树; 先序遍历右子树; | 中序遍历左子树; 访问根节点; 中序遍历右子树; | 后序遍历左子树; 后序遍历右子树; 访问根节点; |
遍历二叉表的三种方法

- 先序遍历结果(根左右):A B D G C E H F
- 中序遍历结果(左根右):D G B A E H C F
- 后序遍历结果(左右根):G D B H E F C A
void InOrder(BiTree T)//中序
{
if (!T)
return;
InOrder(T->lchild);
printf("%c ", T->data);
InOrder(T->rchild);
}
void PreOrder(BiTree T) //先序
{
if (!T)
return;
printf("%c ", T->data);
PreOrder(T->lchild);
PreOrder(T->rchild);
}
void PostOrder(BiTree T) //后序
{
if (!T)
return;
PostOrder(T->lchild);
PostOrder(T->rchild);
printf("%c ", T->data);
}
二叉树的层次遍历
使用队列(易理解):
- 将根结点进队
- 队不空时循环:从队列中出列一个结点*p访问它: 若它有左孩子,则将左孩子结点进队; 若它有右孩子,则将右孩子结点进队;
void LevelOrer(BiTree T)
{
BiTree temp = NULL;
SqQueue Q;
InitQueue(&Q);
if (T) // 先入队根
EntryQ(&Q, T);
while (!IsEmpty(&Q))
{
OutQ(&Q, &temp); // temp暂存弹出值
printf("%c", temp->data); //输出
if (temp->lchild) //在入队temp的左孩子和右孩子
EntryQ(&Q, temp->lchild);
if (temp->rchild)
EntryQ(&Q, temp->rchild);
}
}
先序创建二叉树
void Creat_BiTree_Pre(BiTree *T)
{
//根据输出字符识别虚空节点,'#' 代表虚空节点
char e;
scanf(" %c", &e); //输入字符
if ( e== '#')
*T = NULL; //设置虚空节点
else
{
*T = (BiTree)malloc(sizeof(BiNode));
(*T)->data = e; //生成根结点
Creat_BiTree_Pre(&(*T)->lchild);//构造左子树
Creat_BiTree_Pre(&(*T)->rchild);//构造右子树
}
}
复制二叉树
如果,是空树,递归结束;
否则,复制新结点空间,复制根结点:
- 递归复制左子树
- 递归复制右子树
void Copy(BiTree *Tnew, const BiTree T)
{
if (!T)//如果是空树则返回
{
*Tnew = NULL;
return;
}
else
{
*Tnew = (BiTree)malloc(sizeof(BiNode));
(*Tnew)->data = T->data;
Copy(&(*Tnew)->lchild, T->lchild);
Copy(&(*Tnew)->rchild, T->rchild);
}
}
销毁二叉树
//递归的方式
void Destroy(BiTree *root)
{
//销毁操作必须按照后续遍历的顺序
if (!(*root))
return;
else
{
Destroy(&(*root)->lchild);
Destroy(&(*root)->rchild);
free(*root);
*root = NULL;
}
}
写在最后
👍🏻点赞,你的认可是我创作的动力!
⭐收藏,你的青睐是我努力的方向!
✏️评论,你的意见是我进步的财富!