原文地址: 论文阅读11——《Mutual Boost Network for Attributed Graph Clustering》
作者:Xiaoqiang Yan, Xiangyu Yu, Shizhe Hu, Yangdong Ye
发表时间:预印本
论文地址:https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4195979
代码地址:https://github.com/Xiaoqiang-Yan/MBN
目录
- 创新
- 存在问题
- 解决方案
- 观点
- 模型
- 自编码器模块
- 图自编码器模块
- 表示增强模块
- 自监督模块
- 实验
- 伪代码
- 实验结果
- 结论
创新
存在问题
- 现有区分表示的方法受到
节点和结构特征之间差异的限制。 - 如何保证由
节点和结构特征产生的聚类分配的一致性仍然是一个具有挑战性的问题,这往往会导致聚类性能下降。现有方法忽略了这个问题。
解决方案
- 提出一种新的双通道属性图聚类网络(MBN),它由
自编码器和图自编码器组成,可以相互学习和交互,实现聚类性能的相互提升。 - 设计一种
表示增强机制,以促进异构节点和结构特征的传播和融合。 - 首先提出一种新的
表示增强模块,将来自节点和结构特征的异构信息传播出去,用于学习综合表示。然后通过对比聚类分配,设计了一致性约束,提供了相互指导,使聚类分配趋于一致。最后在一个统一的框架下,以自监督的方式,同时优化表示学习和聚类分配过程。
观点
- 属性图聚类任务的
关键前提是学习节点的判别表示。 - 现有的GCN虽然取得了很大的成功,但是由于过度依赖于邻居节点的信息集成,在
拓扑与节点特征的融合方面并不理想,存在过平滑问题。 - 自编码器和图自编码器学到的表示融合后是全面和可靠的,可以产生高置信度的辅助聚类分配。
- 现有的方法不能充分利用节点和拓扑结构来学习鉴别性的表示,他们不能保证由异构节点和结构特征产生的不同分配的聚类一致性,从而导致聚类性能不佳。
模型
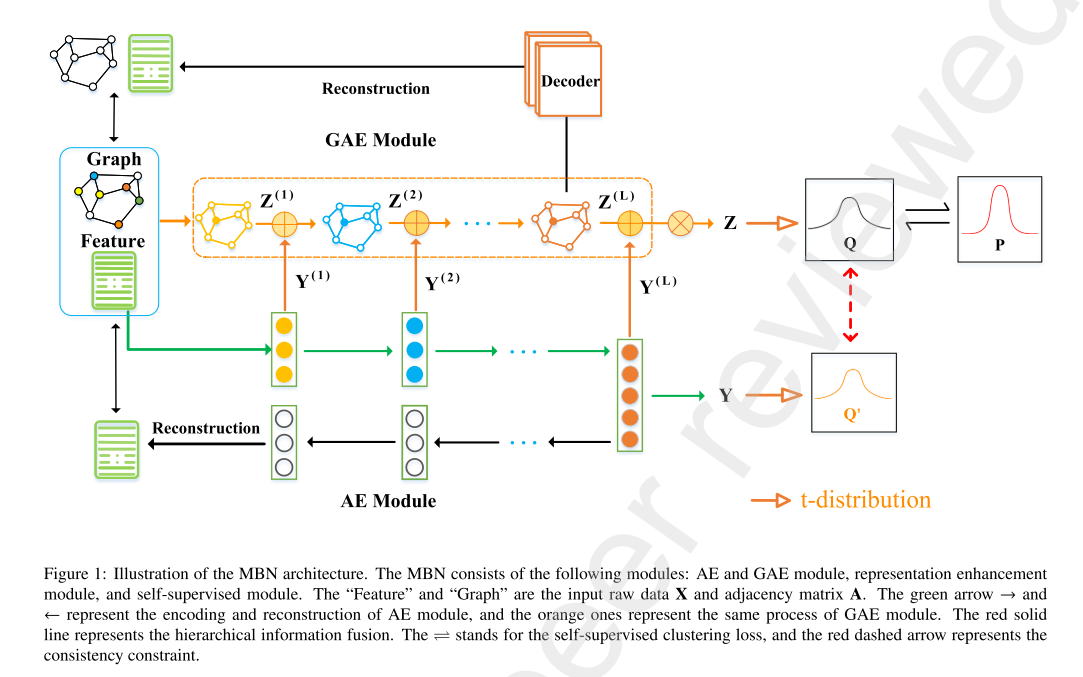
自编码器模块
没啥好说的了,写了这么多篇论文阅读,都有自编码器模块,可以去前面的文章看。最终得到一个属性的重建损失,用于后面的模型训练。
图自编码器模块
与DFCN中IGAE模块类似,使用图卷积作为编码器部分,同时解码器部分也用图卷积:
Z
(
l
+
1
)
=
φ
(
A
~
Z
(
l
)
U
e
(
l
)
)
Z
^
(
k
+
1
)
=
φ
(
A
~
Z
(
k
)
U
d
(
k
)
)
\begin{aligned} Z^{(l+1)}&=\varphi(\widetilde{A}Z^{(l)}U_e^{(l)}) \\ \hat{Z}^{(k+1)}&=\varphi(\widetilde{A}Z^{(k)}U_d^{(k)}) \end{aligned}
Z(l+1)Z^(k+1)=φ(A
Z(l)Ue(l))=φ(A
Z(k)Ud(k))
重建邻接矩阵:
A
^
=
σ
(
Z
Z
⊤
)
+
σ
(
Z
^
Z
^
⊤
)
\hat{A}=\sigma(ZZ^\top)+\sigma(\hat{Z}\hat{Z}^\top)
A^=σ(ZZ⊤)+σ(Z^Z^⊤)
最后通过以下损失函数进行训练:
L
G
A
E
=
L
f
+
δ
L
a
L
f
=
1
2
N
∥
A
~
X
−
Z
^
∥
2
2
L
a
=
1
2
N
∥
A
~
−
A
^
∥
2
2
\begin{aligned} &L_{GAE} =L_f+\delta L_a \\ &L_f = \frac{1}{2N}\|\widetilde{A}X-\hat{Z}\|_2^2 \\ &L_a = \frac{1}{2N}\|\widetilde{A}-\hat{A}\|_2^2 \end{aligned}
LGAE=Lf+δLaLf=2N1∥A
X−Z^∥22La=2N1∥A
−A^∥22
分别表示GAE的损失函数、特征表示Z的重建损失、邻接矩阵的重建损失。
表示增强模块
用于传播和融合异构节点和结构信息,以获得更全面、更有区分度的表示。该模块包括两个步骤:层间信息传播和结构信息融合。首先,为了从图数据中提取更多的鉴别信息,将节点的纯属性特征集成到GCN中进行结构表示学习,对具有结构信息的特征信息的传播,通过线性计算将AE中的特征注入到GAE模块对应的层,这里说这么多其实还是SDCN中的传递算子进行的操作,公式也不展示了。
为了进一步提高表示质量,利用一个类似图卷积的算子来从邻居中集成结构信息:
Z
=
A
~
(
Y
(
L
)
+
Z
(
L
)
)
Z=\widetilde{A}(Y^{(L)}+Z^{(L)})
Z=A
(Y(L)+Z(L))
其实就是用归一化拉普拉斯算子
A
~
\widetilde{A}
A
对自编码器的最后一层嵌入表示
Y
(
L
)
Y^{(L)}
Y(L)和图自编码器的最后一层嵌入表示
Z
(
L
)
Z^{(L)}
Z(L)进行信息聚合的操作,所谓类似图卷积,就是将图卷积神经网络中的参数矩阵看作单位矩阵
I
I
I。
自监督模块
这里与之前模型不同的是,没有使用自编码器嵌入
Y
Y
Y的辅助分布,而是使用图自编码器嵌入
Z
Z
Z的目标分布
Q
Z
Q_Z
QZ和辅助分布
P
Z
P_Z
PZ,对应的损失函数为:
L
c
l
u
=
K
L
(
P
Z
∥
Q
Z
)
=
∑
i
∑
j
p
i
j
log
p
i
j
q
i
j
L
c
o
n
=
K
L
(
Q
Z
∥
Q
Y
)
=
∑
i
∑
j
q
i
j
log
q
i
j
q
i
j
′
\begin{aligned} L_{clu}&=KL(P_Z\|Q_Z)=\sum\limits_i\sum\limits_jp_{ij}\log\frac{p_{ij}}{q_{ij}} \\ L_{con}&=KL(Q_Z\|Q_Y)=\sum\limits_i\sum\limits_jq_{ij}\log\frac{q_{ij}}{q_{ij}'} \end{aligned}
LcluLcon=KL(PZ∥QZ)=i∑j∑pijlogqijpij=KL(QZ∥QY)=i∑j∑qijlogqij′qij
总的损失函数:
L
=
L
r
e
c
+
α
L
c
l
u
+
β
L
c
o
n
L
r
e
c
=
L
G
A
E
+
L
A
E
\begin{aligned} &L=L_{rec}+\alpha L_{clu} + \beta L_{con} \\ &L_{rec}=L_{GAE}+L_{AE} \end{aligned}
L=Lrec+αLclu+βLconLrec=LGAE+LAE
最终的聚类结果使用自编码器嵌入
Y
Y
Y的目标分布
Q
Y
Q_Y
QY作为聚类结果:
r
i
=
arg
max
j
q
i
j
r_i=\arg\max_jq_{ij}
ri=argjmaxqij
实验
伪代码

实验结果
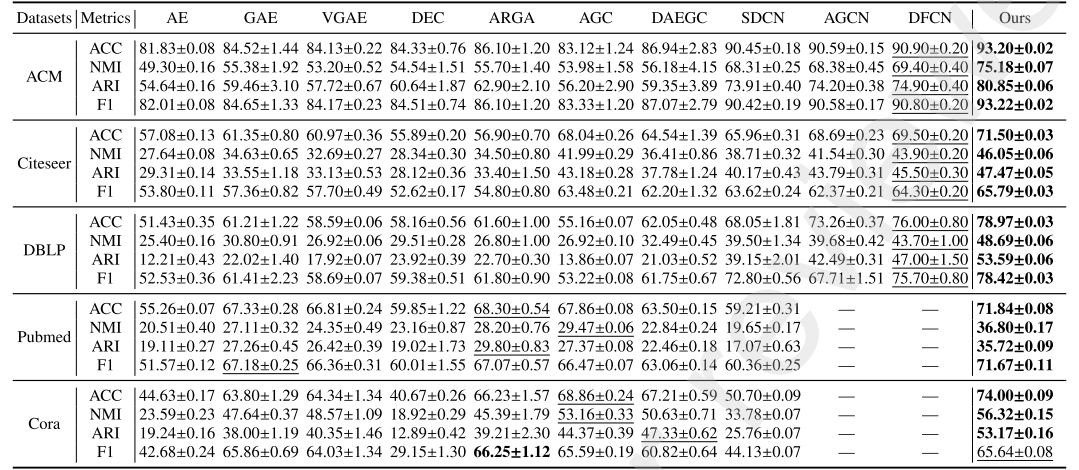
结论
提出一种新的双通道属性图聚类网络(MBN),该网络由自编码器和图自编码器组成,他们可以相互学习和交互。
MBN的优点:
- 利用所提出的表示增强模块,传播并融合来自节点特征和图结构的有价值的异构信息,用于识别图表示学习
- 提出一致性约束目标,以提高不同任务之间的聚类一致性。
- 设计了一个自监督模块,在一个统一的框架中同时优化图聚类性能和表示学习。