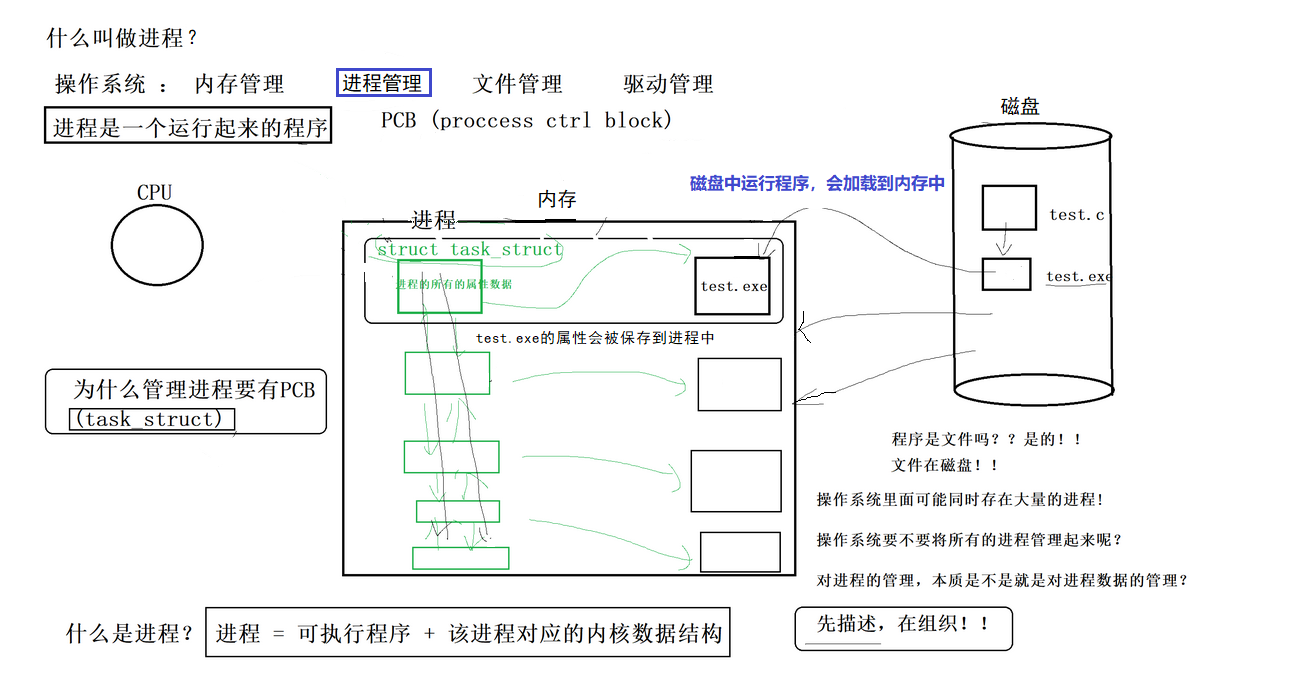
概述

近几年扩散模型不断涌现，但都来源于一个基础模型：DDPM（Denoising Diffusion Probabilistic Model）。扩散模型本质是生成模型，过去我们常用的生成模型包括GAN和VAE，利用随机噪声生成图像样本。GAN和VAE有一个共同点，它们都是使用一个网络直接一步式生成结果，如果要获得好的生成结果，不得不追求更复杂的网络，但是这会导致训练困难。

相反，DDPM中包含了一个新的想法，对于前向过程，我们对 $x_0$ 逐步加噪声，得到一系列的数据$x_{t-1},x_t,...,x_T$。如下图所示：

虽然前向步骤和图像生成没有关系，但这是构建训练样本GT的重要步骤。

前向过程的每个时刻$t$只与时刻$t-1$有关，所以可以看作马尔可夫过程，扩散的目的是通过马尔可夫过程将$x_0$逐渐映射到多维正态分布（高斯噪声）。其中每一步的随机过程为$q(x_t|x_{t-1})$，这个过程由我们自己定义（是已知的），通常，我们把加噪声的过程定义为（利用了重参数方式）：$$x_t={\alpha }_t{x}_{t-1}+{\beta }_t{ϵ}_t,{ϵ}_t\sim N(0,I)$$其中，${\alpha }_t,{\beta }_t$是系数，并且满足调和关系：$${\alpha }_t^2+{\beta }_t^2=1$$其中，${\beta }_t$是随着$t$的增加不断变大的。

从$x_T$到$x_0$的过程是扩散的逆向过程，图像慢慢从高斯噪声变换到正常图像，每一步的随机过程为$q(x_{t-1}|x_t)$，该过程是未知的，因此扩散模型要做的是定义一个可学习的为$p_{\theta }(x_{t-1}|x_t)$的逆向过程，通过优化参数$\theta$，使得该过程尽可能接近真实逆向过程$q(x_{t-1}|x_t)$，从而使我们能通过一个高斯噪声生成正常图像。

前向过程

DDPM定义的前向过程为：$$q(x_t|x_{t-1})=N(x_t;\sqrt{{\alpha }_t}{x}_{t-1},{\beta }_{t}I)$$由于高斯分布的性质，可以得到：$$q(x_t|x_0)=N(x_t;\sqrt{{\overline{\alpha }}_t}{x}_0,(1-{\overline{\alpha }}_t)I)$$其中$I$为单位矩阵，${\overline{\alpha }}_t={\prod }_{i=1}^t{\alpha }_i$，由于${\alpha }_t$是逐渐减小的，所以当$t$接近无穷时，$q(x_t|0)=N(x_t;0,I)$，即此时$x_t$服从标准正态分布。

---

关于$N(x_t;0,I)$，指的是$x_t\sim N(0,I)$。

---

逆向过程

对于逆向的随机过程$q(x_{t-1}|x_t)$是无法求出的，但是在已知$x_0$的情况下，我们可以通过贝叶斯公式求出：$$\begin{gathered} q(x_{t-1}|x_t,x_0)=q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)} \\ =N(x_{t-1};{\tilde{\mu }}_t(x_t,x_0),{\tilde{\beta }}_{t}I) \end{gathered}$$其中：$${\tilde{\mu }}_t(x_t,x_0)=\frac{\sqrt{{\alpha }_t(1-{\overline{\alpha }}_{t-1})}}{1-{\overline{\alpha }}_t}{x}_t+\frac{\sqrt{{\overline{\alpha }}_{t-1}}{\beta }_t}{1-{\overline{\alpha }}_t}{x}_0$$$${\tilde{\beta }}_t=\frac{1-{\overline{\alpha }}_{t-1}}{1-{\overline{\alpha }}_t}{\beta }_t$$对随机过程$q(x_t|x_0)$使用重参数方法，得到$x_t$关于$x_0$的表达式，并且表达式中包含一个高斯噪声${ϵ}_t\sim N(0,I)$，再转换一下变量，就得到：$$x_0=\frac{x_t-\sqrt{1-{\overline{\alpha }}_t}{ϵ}_t}{\sqrt{{\alpha }_t}}$$把$x_0$代入${\tilde{\mu }}_t(x_t,x_0)$得到：$${\tilde{\mu }}_t=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{{\beta }_t}{\sqrt{1-{\overline{\alpha }}_t}}{ϵ}_t)$$到这里，我们发现，如果我们假设我们知道了$x_0$，我们可以根据$q(x_{t-1}|x_t,x_0)$采样出$x_{t-1}$，但问题在于，在重参数过程中有一个随机噪声${ϵ}_t$，尽管它服从标准正态分布，但是要还原到$x_0$，我们必须确保逆向过程的每一步都能准确预测出每一步的$ϵ$的具体噪声值。所以，DDPM使用UNet来预测这个噪声值。

DDPM

我们先设：$$p_{\theta }(x_{t-1}|x_t)=N(x_{t-1};{\mu }_{\theta }(x_t,t),{\tilde{\beta }}_{t}I)$$而${\mu }_{\theta }(x_t,t)$的表达式为：$${\mu }_{\theta }(x_t,t)=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{{\beta }_t}{\sqrt{1-{\overline{\alpha }}_t}}{ϵ}_{\theta }(x_t,t))$$其中，${ϵ}_{\theta }$就是这个UNet，$\theta$是网络参数，网络输入$x_t$和$t$，然后预测出该时刻的噪声${\widehat{ϵ}}_t$，然后根据下面式子从$x_t$回到$x_{t-1}$：$$x_t={\alpha }_t{x}_{t-1}+{\beta }_t{ϵ}_t\to x_{t-1}=\frac{x_t-{\beta }_t{\widehat{ϵ}}_t}{{\alpha }_t}$$因此，对于训练，只需要让UNet在每个时刻的输出拟合前向过程对应时刻采样出的噪声即可：$$L_t=||{ϵ}_t-{\widehat{ϵ}}_t||=||{ϵ}_t-\widehat{ϵ}(x_t,t)||$$