CSDN话题挑战赛第2期
参赛话题:学习笔记
前言
💖作者:龟龟不断向前
✨简介:宁愿做一只不停跑的慢乌龟,也不想当一只三分钟热度的兔子。
👻专栏:C++初阶知识点👻工具分享:
- 刷题: 牛客网 leetcode
- 笔记软件:有道云笔记
- 画图软件:Xmind(思维导图) diagrams(流程图)
如果觉得文章对你有帮助的话,还请点赞,关注,收藏支持博主🙊,如有不足还请指点,博主及时改正
函数递归
文章目录
- 函数递归
- 🚀1.递归的概念
- 🍉史上最简单的递归
- 🚀2.递归的必要条件
- 🍉举例:递归设计循环输出数的每一位
- 🍉递归展开图分析递归
- 🚀3.初学递归必做练习题
- 🍉递归实现strlen
- 🍉递归求n的阶乘
- 🍉求第n个斐波那契数
- 🍉递归实现计算n的k次方
- 🍉递归实现逆置字符串
🚀1.递归的概念
上次我们介绍了函数的嵌套调用,一个函数的定义中除了可以调用另一个函数,还可以调用其本身。程序调用自身的编程技巧称为递归( recursion)。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
递归的主要思考方式在于:把大事化小
🍉史上最简单的递归
#include<stdio.h>
int main()
{
printf("hello world\n");
main();
return 0;
}
虽然说是递归,但其实是一个死递归。就像一个循环设计成死循环一样,是没有意义的。main函数调用main函数,该程序会一直输出hello world,直到程序挂掉(栈溢出stack overflow)。
解释:
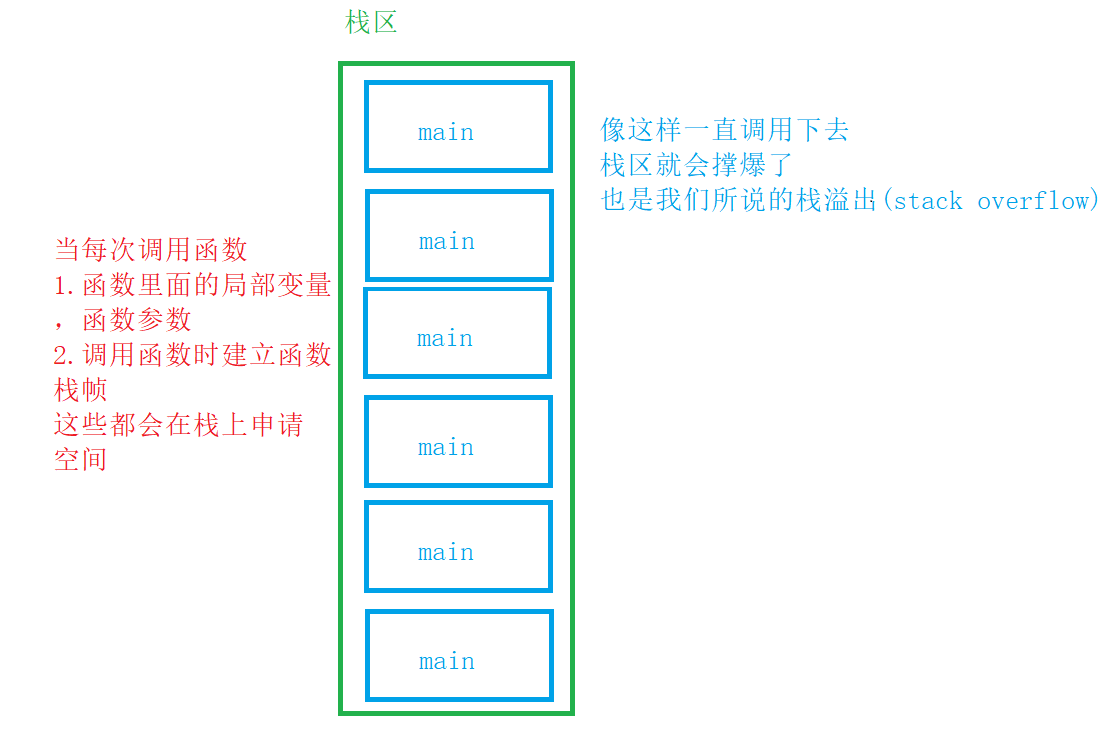
咱们调用的时候也会有栈溢出的报错
🚀2.递归的必要条件
在学习循环时,循环也有其对应的循环必要条件,这样才能构成一个功能完整的可控的循环。
相应地,想要形成一个功能完成的可控的递归,也有其对应的递归必要条件。
- 存在限制条件,当满足这个限制条件的时候,递归便不再继续。
- 每次递归调用之后越来越接近这个限制条件。
🍉举例:递归设计循环输出数的每一位
递归的核心:
- 将大事化小,大问题->小问题->最小问题(而且这些小问题的处理方式逻辑是类似的)
- 到分解成最小子问题时候的处理方法
例如将顺序打印1234,给大事化小
- 顺序打印1234 -> 顺序打印123 + 输出1234的个位(因为4很好输出,就是1234的个位)
- 顺序打印123 -> 顺序打印12 + 输出123的个位
- 顺序打印12 -> 顺序打印1 + 输出12的个位
顺序打印一位数已经是最小子问题,最小子问题直接打印其个位即可
#include<stdio.h>
void seq_print(int n)
{
if (n > 9)
{
seq_print(n / 10);
}
printf("%d ", n % 10);
}
int main()
{
seq_print(1234);
return 0;
}
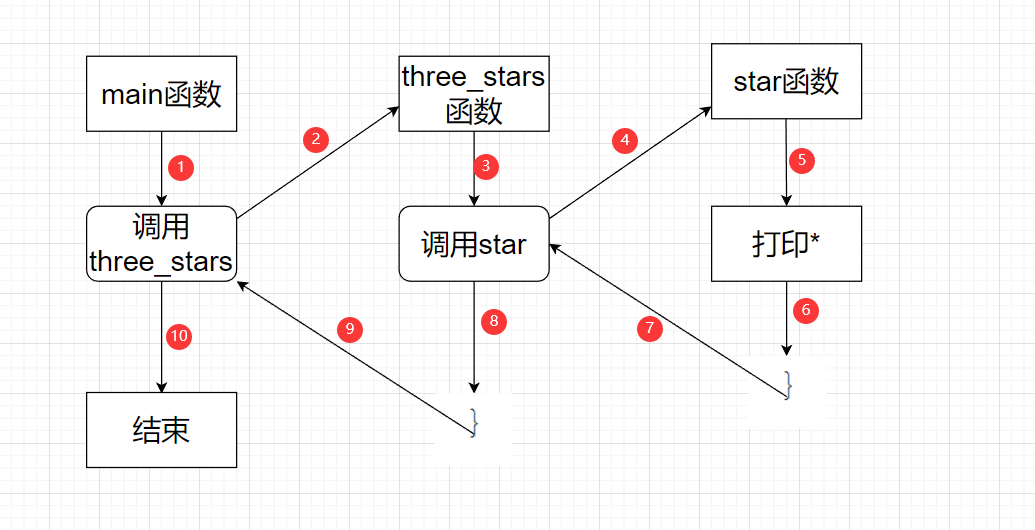
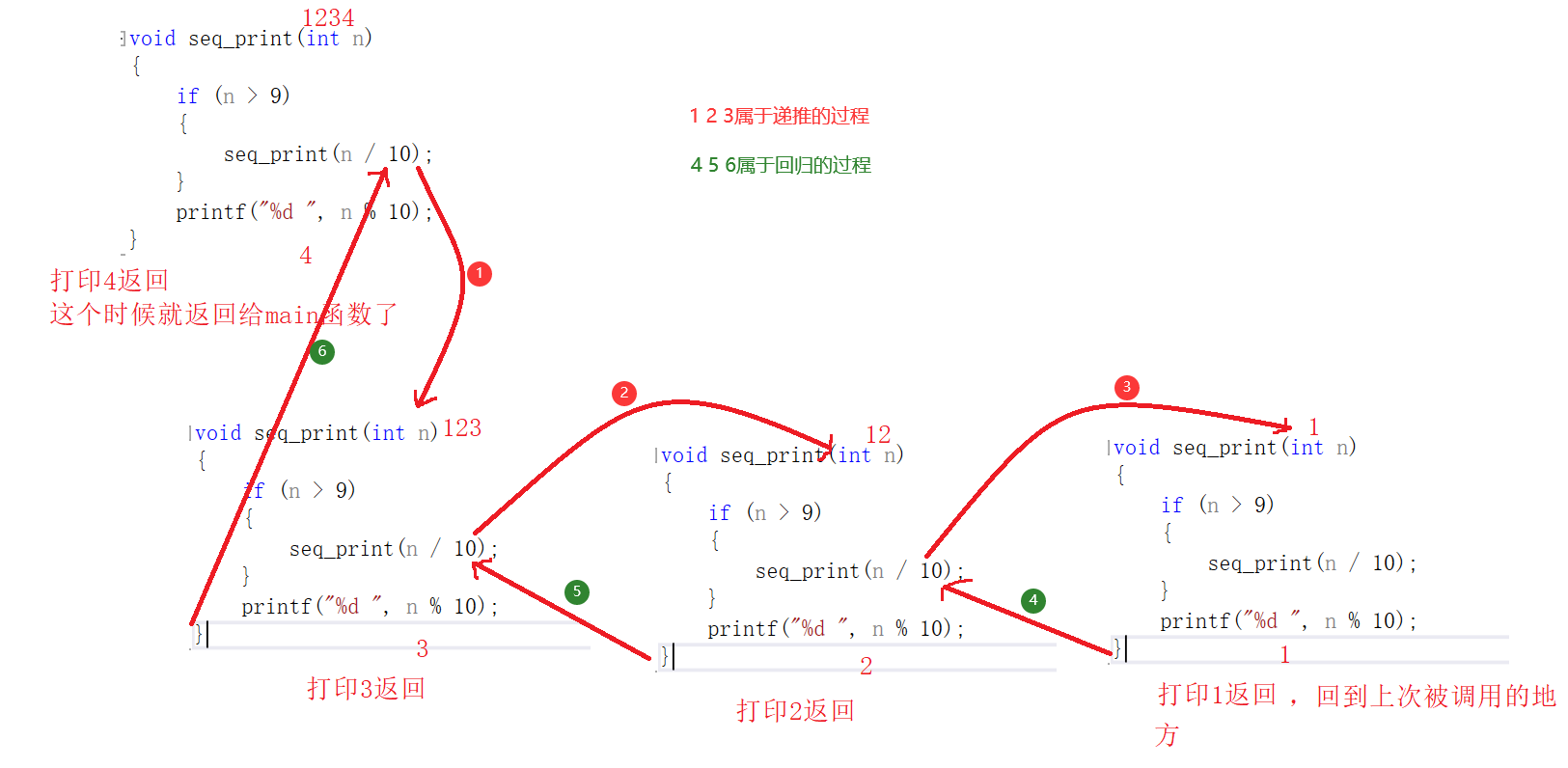
🍉递归展开图分析递归
递归,这个名字取得非常的精简,顾名思义:递推,回归!它即存在一个递推的过程,也有有一个回归的过程。
函数嵌套调用的过程:
图解
🚀3.初学递归必做练习题
🍉递归实现strlen
模拟实现
strlen,迭代版本(非递归版本),以及递归版本
非递归版本:

#include<stdio.h>
int my_strlen(char* str)
{
int count = 0;
while (*str != '\0')
{
count ++;
str++;
}
return count;
}
int main()
{
char str[] = "hello world";
int len = my_strlen(str);
printf("len = %d\n", len);
return 0;
}
递归版本:
还是那个核心,大事化小,递归逻辑和非递归的逻辑是类似的,只是思考角度不一样
如果第一个字符不是
\0,那么字符串的长度为1 + 后面部分字符串的长度
abcdef的长度 -> 1 +bcdef的长度
bcdef的长度 -> 1 +cdef的长度………………
ef的长度 -> 1 + f的长度
f的长度 -> 1 +""的长度最小子问题:
""(空串)的长度返回0即可
#include<stdio.h>
int my_strlen(char* str)
{
if ((*str) == '\0')//最小子问题的处理方式
{
return 0;
}
else
{
return 1 + my_strlen(str + 1);
}
}
int main()
{
char str[] = "hello world";
int len = my_strlen(str);
printf("len = %d\n", len);
return 0;
}
🍉递归求n的阶乘
数学上计算n的阶乘的公式有
- 通项公式:n! = 1 * 2 * 3 * …* n
- 递推公式:n! = n*(n-1)!
而我们递归所需要的就是递推公式,它可以现成的将大事化小
#include<stdio.h>
int Fac(int n)
{
if (n < 2)
{
return 1;
}
else
{
return n*Fac(n - 1);
}
}
int main()
{
int num = 0;
int ret = 0;
scanf("%d", &num);
ret = Fac(num);
printf("%d\n", ret);
return 0;
}
🍉求第n个斐波那契数
斐波那契数列:第一个数和第二个数为1,后面的数是前面两项数字的和,这样的数的组合就是斐波那契数列
例如:1 1 2 3 5 8 13 21 34 55…
非常明显:斐波那契数列的定义已经明确了他的递归公式:F(N) = F(N-1) + F(N-2)
#include<stdio.h>
int Fibonacci(int n)
{
if (n <= 2)
{
return 1;
}
else
{
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
}
//斐波那契数列 1 1 2 3 5 8 13 21
int main()
{
int n = 0;
scanf("%d", &n);
printf("%d\n", Fibonacci(n));
return 0;
}
但是很不幸,上述程序是效率很低的,如果计算45!左右时,都要计算老半天,效率非常低。
解释:
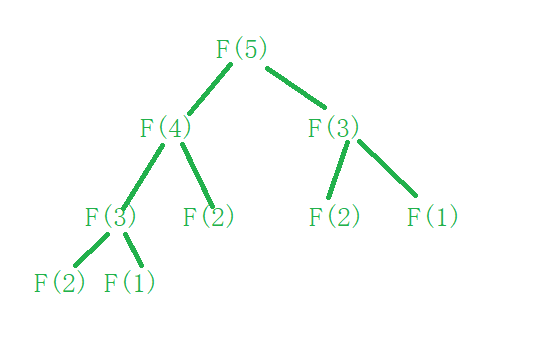
原因是,里面存在着大量的重复计算,比如说你在计算第5个斐波那契数
在计算出F(4)的过程中,其实也会将F(3)给计算出来,可是到了计算右边的F(3)时候,又重复地计算了一遍F(3)
因为该递归计算出来的数,是没有保存的,当数字越来越大,就存在着大量的重复计算,效率也就自然低了
我们可以看一看,当计算40!的时候,计算了多少次F(3)
int count = 0;
int Fibonacci(int n)
{
if (n == 3)
{
++count;
}
if (n <= 2)
{
return 1;
}
else
{
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
}
int main()
{
int n = 0;
scanf("%d", &n);
printf("%d! = %d\n", n, Fibonacci(n));
printf("F(3) = %d\n", count);
//printf("fibo(2) = %d\n", count);
return 0;
}
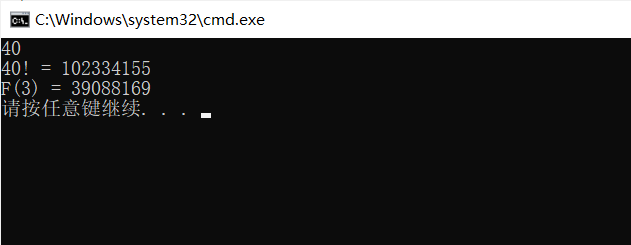
所以,使用递归来实现斐波那契是很低效的,所以咱们要使用迭代。
图解思路:

#include<stdio.h>
int Fibonacci(int n)
{
if (n <= 2)
{
return 1;
}
int a = 1;
int b = 1;
int c = 0;
while ((n--) > 2)
{
c = a + b;
a = b;
b = c;
}
return c;
}
//斐波那契数列 1 1 2 3 5 8 13 21
int main()
{
int n = 0;
scanf("%d", &n);
printf("%d! = %d\n", n, Fibonacci(n));
return 0;
}
小扩展:,其实大家平时听到的,青蛙跳台问题,生兔子问题实质都是斐波那契数列问题
这是剑指offer的题目哟!
#include<stdio.h>
int numWays(int n) {
size_t left = 1;
size_t right = 1;
if(n < 2)
{
return 1;
}
while((n--) >= 2)
{
size_t ret = (left + right)%(1000000007);
left = right;
right = ret;
}
return right;
}
🍉递归实现计算n的k次方
大家肯定可以想到累乘法–将n累乘k次即可
递归思路:n^k = n^(k-1) * k
n的k次方等于n的k-1次放乘以k
#include<stdio.h>
double Pow(double n, int k)//n的k次方
{
if (k < 0)
{
k = -k;
n = 1.0 / n;
}
if (k == 0)
{
return 1.0;
}
if (k == 1)
{
return n;
}
return n * Pow(n, k - 1);
}
int main()
{
printf("%f\n", Pow(2, 3));
printf("%f\n", Pow(2, -3));
return 0;
}
解释:
这里需要特殊处理一下k是负数,k是0的情况,如果k是负数,我们要将n变成1/n,k再取正数。
其实,这还是一道剑指offer上面的题,有个大佬想出了一种特别高效的算法,有兴趣的同学可以看一下,真的叫人拍案叫绝
🍉递归实现逆置字符串
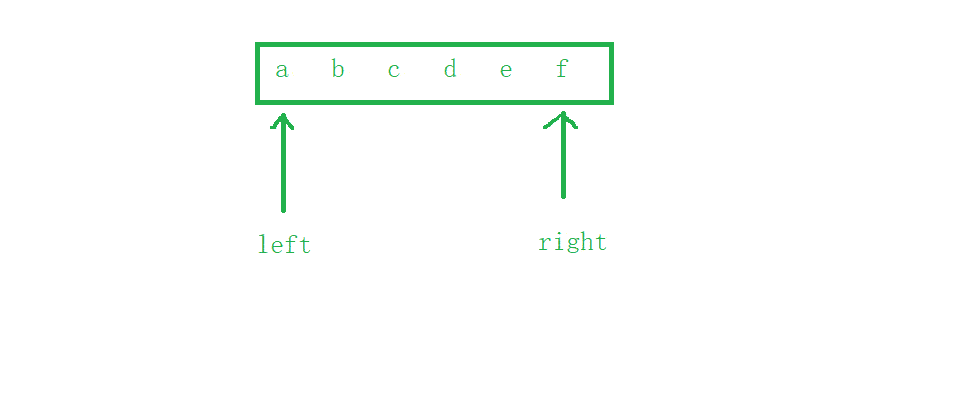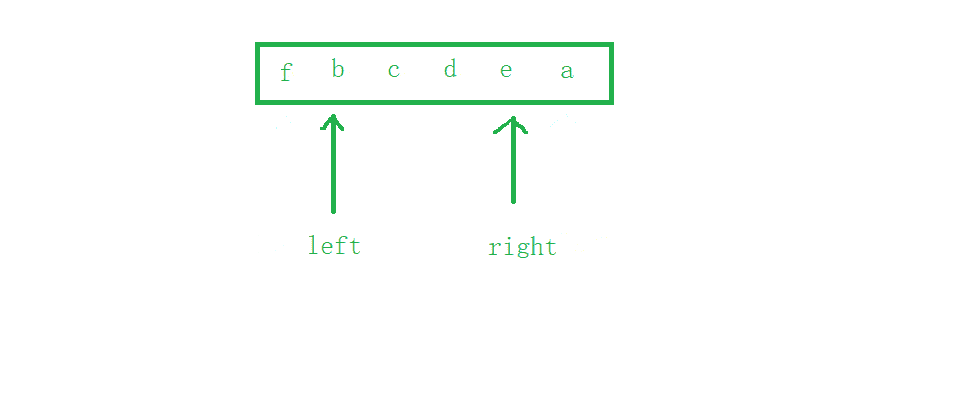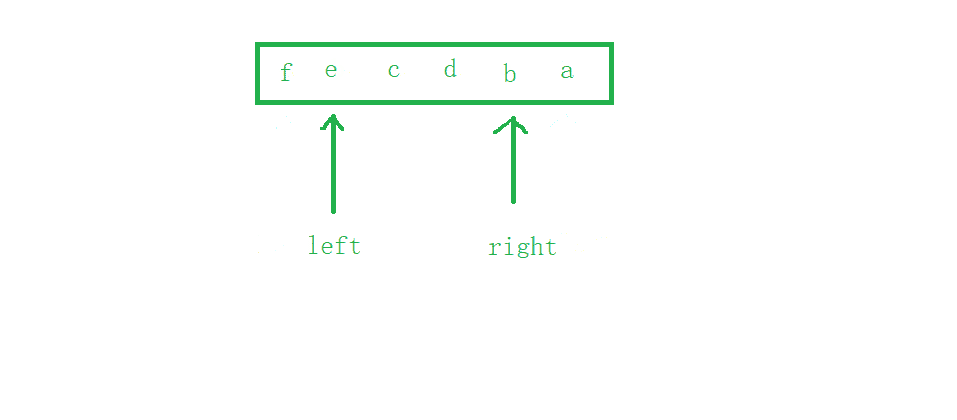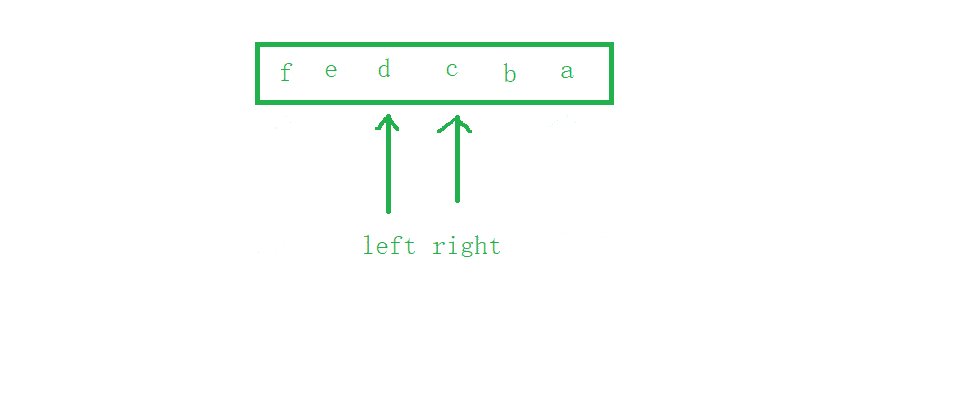
非递归版本:
使用两个下标来实现左右字符交换即可,字符串的后面是放了
\0的,图中没画
#include<stdio.h>
#include<string.h>
void reverse_string(char str[])
{
int left = 0;
int right = strlen(str) - 1;
while (left < right)
{
char tmp = str[left];
str[left] = str[right];
str[right] = tmp;
++left;
--right;
}
}
int main()
{
char str[] = "abcdef";
printf("逆置前\n");
printf("%s\n", str);
reverse_string(str);
printf("逆置后\n");
printf("%s\n", str);
return 0;
}
递归版本:
实现逻辑和非递归是一致的
思考角度:逆置
abcdef-> 交换a和f+ 逆置bcde逆置
bcde-> 交换b和e+ 逆置cd逆置
cd-> 交换b和e+ 逆置""最小子问题:空串或者串的长度为1,不做任何处理
想必大家都会交换
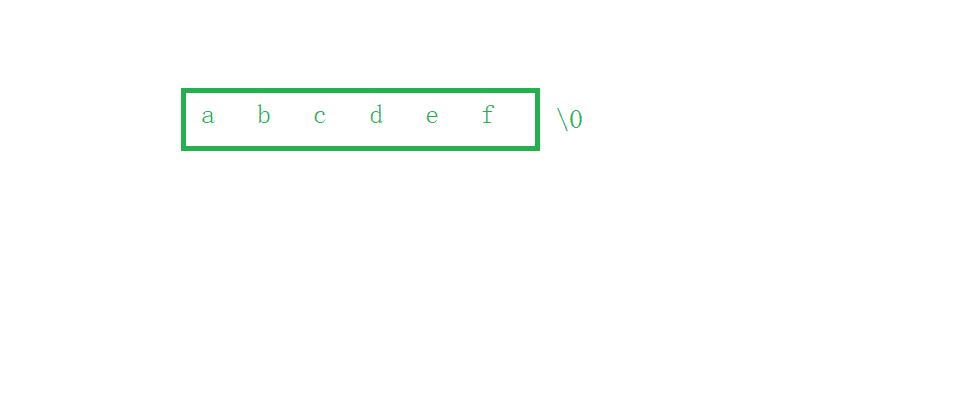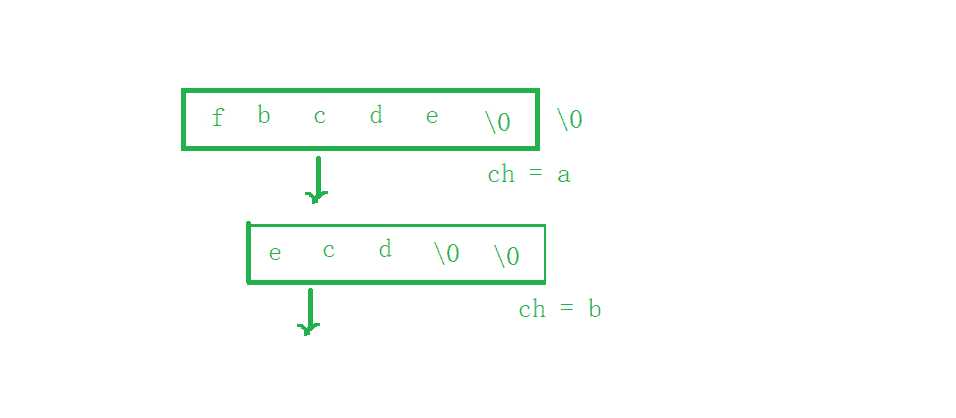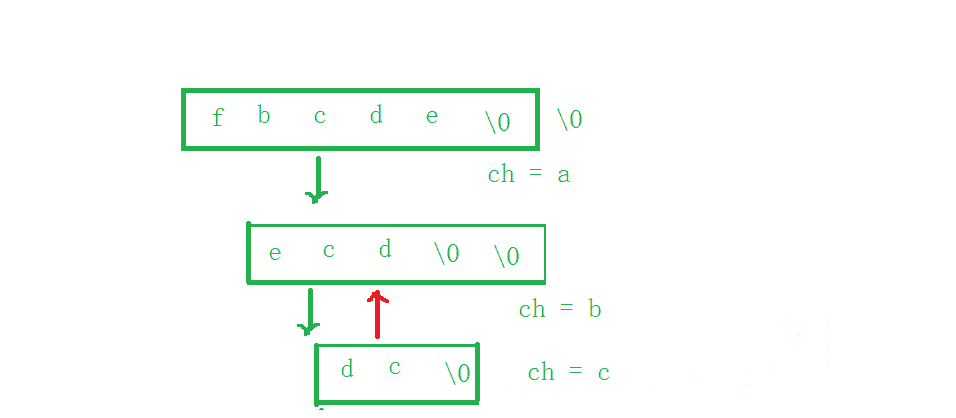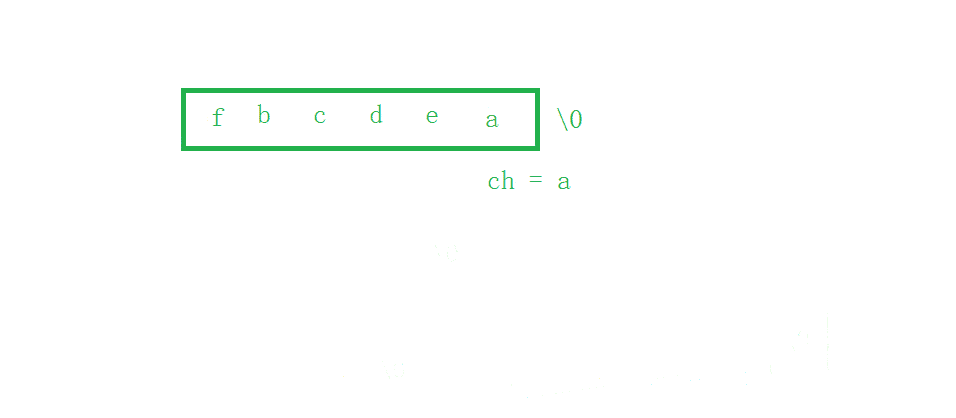
a和f的操作,但是如何实现逆置bcde的操作呢,因为C字符串是以\0结尾的,如果先完成a和f的交换,那么如何取到bcde字符串?方法:a和f的交换先完成一部分:
- 提出a(保存a字符)
- 将f放进原来a的位置
- 后面的位置放
\0–为了我们可以控制第4步的逆置- 逆置
bcde- 再将a放到原来f的位置
1 2 5组合起来才是a和f交换的操作,现在将逆置
bcde的步骤,插进交换a和f的中,即可实现递归
图解
#include<string.h>
#include<stdio.h>
void reverse_string(char * string)
{
int len = strlen(string);
if (len > 1)
{
char ch = string[0];//1.将第一个字符保存下来
string[0] = string[len - 1];//2.最后一个字符将第一个字符的位置占据
string[len - 1] = '\0';//3.最后一个位置给上\0便于操作,能实现递归的核心操作
reverse_string(string + 1);//4.子问题
string[len - 1] = ch;//5.将\0的位置用ch补上
}
}
int main()
{
char str[] = "abcdef";
printf("逆置前\n");
printf("%s\n", str);
reverse_string(str);
printf("逆置后\n");
printf("%s\n", str);
return 0;
}
本片文章就讲到这里,如果不好理解递归的话,建议大家多画画递归展开图,对递归的递推和回归有个一个更深入的理解当然了,递归的路还很长,在以后的算法和数据结构中都会遇到,相信不同阶段大家会有不同的理解。希望能帮助到大家!
下期递归小实战–实现汉诺塔问题,咱们下期间!