摘要

基于势能的奖励塑形可以显著降低学习最优策略所需的时间，并且在多agent系统中，可以显著提高最终联合策略的性能。已经证明，它不会改变一个agent单独学习的最优策略或多个agent一起学习的纳什均衡。

------然而，现有证明的一个局限性是假设状态的势能在学习期间不会动态变化。这种假设经常被打破，特别是如果奖励塑形函数是自动生成的。

------在本文中，我们证明并演示了一种扩展基于势能的奖励塑形的方法，以允许动态塑形，并在单agent情况下保持策略不变性，在多agent情况下维持一致的纳什均衡。

1. INTRODUCTION

------强化学习agent通常在没有先验知识的情况下实现，然而已经反复表明，向agent通知启发式知识可能是有益的[2，7，13，14，17，19]。这种先验知识可以被编码到agent的初始 $Q - v a l u e$ 或奖励函数中。如果通过一个势能函数来实现，则两者可以等价[23]。

------最初，基于势能的奖励塑形被证明不会改变单个agent的最优策略，该agent提供了仅基于状态的静态势能函数[15]。对该方法的持续兴趣已经扩展了其能力，以在势能基于状态和动作[24]或agent不是单独的，而是在与其他塑形或非塑形agent共同的环境中发挥作用[8]时提供类似的保证。

------然而，所有现有的证明都假定静态势能函数。静态势能函数表示静态知识，因此，在agent学习时不能在线更新。

------尽管理论结果存在这些局限性，但经验工作已经证明了动态势能函数的有用性[10,11,12,13]。在应用基于势能的奖励塑形时，一个常见的挑战是如何设置势能函数。使用动态势能函数的现有工作使这个过程自动化，使方法更容易被所有人访问。

------一些（但不是所有）预先存在的实现(implementations)强制要求其势能函数在agent之前稳定。这一特征可能是基于直觉的论点，即在奖励函数这样做之前，agent无法收敛[12]。然而，正如我们将在本文中所展示的，尽管存在额外的动态奖励，但只要它们是给定的形式，agent就可以收敛。

------我们的贡献是证明动态势能函数如何不改变单agent问题域的最优策略或多agent系统（MAS）的纳什均衡。该工作证明了动态势能函数的现有使用是合理的，并解释了在从未保证额外奖励收敛的情况下，agent如何仍然收敛[10]。

------此外，我们还将证明，通过允许状态的势能随时间变化，基于动态势能的奖励塑形并不等同于Q表初始化。相反，它是一个独特的工具，对于希望持续影响agent探索的开发人员非常有用，同时保证不会改变agent或团队的目标。

------在下一节中，我们将介绍所有相关的背景材料。在第3节中，我们提出了两个关于动态势能函数对基于势的奖励塑形中现有结果的影响的证明。随后，在第4节中，我们通过在单agent和多agent问题域中实证证明动态势能函数来阐明我们的观点。论文最后总结了论文的主要结果。

2. PRELIMINARIES

在本节中，我们将介绍本文所基于的所有相关现有工作。

2.1 Reinforcement Learning

------强化学习是一种范式，它允许agent从与环境的互动中通过奖励和惩罚进行学习[21]。从环境接收的数字反馈用于改进agent的动作。强化学习领域的大部分工作将马尔可夫决策过程（MDP）作为数学模型[16]。

------MDP是一个元组< $S, A, T, R$ >，其中 $s$ 是状态空间， $a$ 是动作空间， $T(s,a,s^′)=Pr(s^′|s,a)$ 是状态 $s$ 中的动作 $a$ 将导致状态s′的概率， $R(s,a,s^′)$ 是当状态 $s$ 中采取的动作 $a$ 导致状态 $s'$ 转换时收到的立即奖励 $r$ 。解决MDP的问题是找到一个策略（即，从状态到动作的映射），使累积的奖励最大化。当环境动力学(environment dynamics)（转移概率和奖励函数）可用时，可以使用策略迭代来解决此任务[3]。

------当环境动态不可用时，与大多数实际问题领域一样，策略迭代无法使用。然而，迭代方法的概念仍然是大多数强化学习算法的主干。这些算法应用所谓的时间差更新来传播关于状态值 $V (s)$ 或状态-动作对 $Q (s, a)$ 的信息[20]。这些更新基于特定状态或状态-动作值的两个时间上不同的估计的差异。 $Q - l e a r n i n g$ 算法就是这样一种方法[21]。每次转换后， $s,a)→(s^′,r)$ ，在环境中，它通过以下公式更新状态动作值：
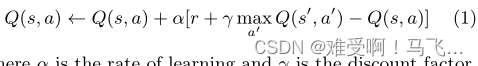
在这里插入图片描述

------其中， $α$ 是学习率， $γ$ 是折扣系数。它修改了状态 $s$ 中采取动作 $a$ 的值，当执行该动作后，环境返回奖励 $r$ ，并移动到新的状态 $s^′$ 。

------假设每个状态-动作对经历无限次，则奖励是有界的，并且agent的探索和学习率降低到零，Q-learning agent的值表将收敛到最优值 $Q^∗$ [22].
2.1.1 Multi-Agent Reinforcement Learning
------强化学习在MAS(多智能体系统)中的应用通常采用两种方法之一；多个agent学习器或联合动作学习器[6]。后者是一组多agent特定算法，旨在考虑其他agent的存在。前者是部署多个agent，每个agent使用单个agent强化学习算法。

------多个agent学习器假设任何其他agent都是环境的一部分，因此，当其他人同时学习时，环境似乎是动态的，因为在状态 $s$ 中采取行动a时，随着时间的推移，转变的概率会发生变化。为了克服动态环境的出现，开发了联合动作学习器，扩展了他们的价值函数，以考虑每个状态下所有agent的每个可能行动组合的价值。

------然而，通过联合行动学习打破了MAS的一个基本概念，即每个agent都是自我激励的，因此可能不同意广播他们的行动选择。此外，考虑联合作用会导致必须在向系统中添加每个附加agent时计算的值的数量呈指数增长。出于这些原因，这项工作将侧重于多个个体学习器，而不是联合行动学习器。然而，这些证明可以扩展到涵盖联合行动学习器。

------与目标是最大化个人奖励的单一agent强化学习不同，当部署多个自我激励的agent时，并非所有agent都能获得他们的最大奖励。相反，必须做出一些妥协，通常该系统旨在收敛到纳什均衡[18]。

------为了对MAS进行建模，单agent MDP变得不充分，而需要更一般的随机博弈（SG）[5]。n个agent的SG是一个元组< $S,A_1,...,A_n;T,R_1,...,R_n$ > ，其中 $S$ 是状态空间， $a_i$ 是 $agent_i$ 的动作空间， $T(s,a_{i,...n},s')=Pr(s'|s,a_{i,...n})$ 是状态 $s$ 中的联合动作 $a_{i,...n}$ 将导致状态 $s^′$ 的概率， $R_i(s,a_i,s^′)$ 是 $agent_i$ 在状态 $s$ 中采取动作 $a_i$ 导致向状态 $s^′$ 过渡时收到的即时奖励[9]。
------通常，强化学习agent，无论是单独部署还是共享环境，都是在没有事先知识的情况下部署的。假设开发人员不知道agent的行为。然而，通常情况并非如此，agent可以从开发人员对问题领域的理解中受益。

------向强化学习传授知识的一个常见方法是奖励塑形，我们将在下一小节更详细地讨论这个话题。

2.2 Reward Shaping

------奖励塑形的想法是提供一个代表先验知识的额外奖励，以减少次优动作的数量，从而减少学习所需的时间[15，17]。这个概念可以用 $Q - l e a r n i n g$ 算法的以下公式表示：
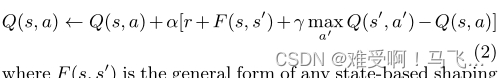
在这里插入图片描述
------其中 $F(s,s^′)$ 是任何基于状态的塑形奖励的一般形式。

------尽管奖励塑形在许多实验中都很强大，但很快就发现，如果使用不当，它会改变最佳策略[17]。为了解决这些问题，提出了基于势能的奖励塑形[15]，作为在源状态 $s$ 和目标状态 $s^′$ 上定义的某些势能函数 $Φ$ 的差：
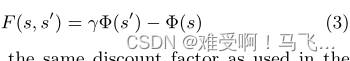
在这里插入图片描述
------其中 $γ$ 必须是agent更新规则中使用的相同折扣因子(参见方程1)。

------Ng等人[15]证明，根据等式3定义的基于势能的奖励塑形保证了学习策略，该策略等同于在无限和有限范围MDP中学习的没有奖励塑形的策略。Wiewiora[23]后来证明，当使用相同的势能函数初始化后一个agent的价值函数时，具有基于势能的奖励塑形和没有基于知识的Q-table初始化的agent学习将与没有奖励塑形的agent行为相同。

-------这些证明，以及关于基于势能的奖励塑形的所有后续证明，包括本文中提出的证明，需要通过基于优势的策略来选择行动[23]。基于优势的策略根据其价值的相对差异而非其确切价值来选择动作。常见的例子包括贪婪、ǫ-贪婪和Boltzmann soft-max。

2.2.1 Reward Shaping in Multi-Agent Systems

------已经证明，在多agent强化学习中，引入启发式知识也是有益的[2,13,14,19]。然而，这些示例中的一些没有使用基于势的函数来塑形奖励[14,19]，因此，可能会因引入有益的循环策略而受到影响，从而导致收敛到先前在单个agent问题域中所证明的非预期行为[17]。

-------其余基于势能的应用[2,13]表明，收敛到更高值纳什均衡的概率增加。然而，这两个应用都没有考虑保证策略不变性的证明是否适用于多agent强化学习。

------从这一次开始，理论结果[8]表明，虽然Wiewiora对Q表初始化的等价性证明[23]也适用于多agent强化学习，但Ng的策略不变性证明[15]并不适用。基于多agent势能的奖励塑形可以改变一组agent将学习的最终策略，但不会改变系统的纳什均衡。

2.2.2 Dynamic Reward Shaping

------奖励塑形通常是使用领域特定的启发式知识[2,7,17]针对每个新环境定制实现的，但已经进行了一些尝试来将[10,11,12,13]知识编码自动化为塑形奖励函数。

------所有这些现有方法都会在agent学习时改变在线状态的势能。现有的单agent[15]和多agent[8]都没有证明理论结果考虑这种动态塑形。

------然而，已经发表了一种观点，即势能函数必须在agent能够收敛之前收敛[12]。在大多数实现中，这种方法已被应用[11,12,13]，但在其他实现中，稳定性从未得到保证[10]。在这种情况下，尽管有共同的直觉，agent仍然被视为收敛到最优策略。

------因此，与现有观点相反，尽管奖励不断变化，agent的策略仍有可能趋同。在下一节中，我们将证明这是如何实现的。

3. THEORY

------在本节中，我们将讨论动态势能函数对基于势的奖励塑形中三个最重要的现有证明的影响。具体而言，在第3.1小节中，我们讨论了单agent问题域中策略不变性的理论保证[15]和多agent问题域的一致纳什均衡[8]。稍后，在第3.2小节中，我们将讨论Wiewiora对Q表初始化的等价证明[23]。

3.1 基于动态势能的奖励塑形可以维持现有的保证

------为了扩展基于势能的奖励塑形以允许动态势能函数，我们扩展方程3以使用时间作为势能函数Φ的参数。非正式地，如果势能差是根据访问时的状态势能计算的，则策略不变或一致纳什均衡的保证仍然存在。正式地：
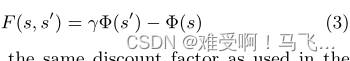
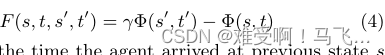
在这里插入图片描述

------其中 $t$ 是agent到达前一状态s的时间， $t^′$ 是到达当前状态 $s^′$ 时的当前时间（即t＜t′）。

------为了证明单agent情况下的策略不变性和多agent情况中的一致纳什均衡，足以证明塑形agent在遵循固定的状态和动作序列时将获得的回报等于非塑形agent遵循相同序列时将收到的回报减去序列中第一个状态的可能性[1,8]。

------因此，让我们考虑任意agenti在没有塑形的情况下在折扣框架中经历序列 $\bar{s}$ 时的返回Ui。正式地：
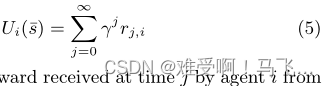
在这里插入图片描述
------其中 $r_{j,i}$ 是 $agent_i$ 在时间 $j$ 从环境接收的奖励。给定此返回定义，真实 $Q$ 值可通过以下公式正式定义：

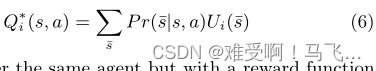
------现在考虑相同的agent，但通过添加等式4中给出的形式的基于动态势能的奖励函数来修改奖励函数。经历相同序列 $\bar{s}$ 的塑形agent $U_{i,Φ}$ 的回报为：
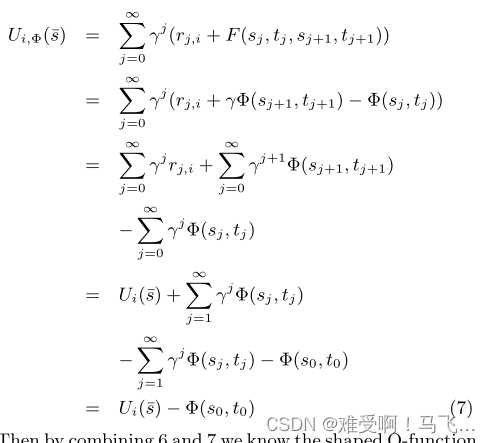
在这里插入图片描述
------然后把6和7结合起来，我们知道塑形的 $Q$ 函数是:

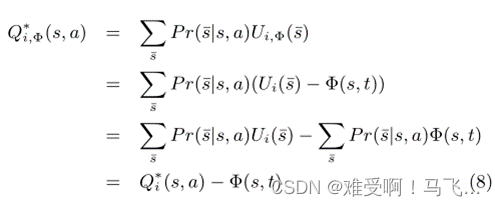
------其中t是当前时间。

------由于原始Q值和塑形Q值之间的差异不取决于所采取的动作，因此在任何给定状态下，无论塑形如何，最佳（或最佳响应）动作都保持恒定。因此，我们可以得出结论，策略不变性和一致纳什均衡的保证仍然存在。

3.2 基于动态势的奖励塑形与 Q 表初始化不等价

------在单agent[23]和多agent[8]强化学习中，具有静态势能函数的基于势能的奖励塑形等同于初始化agent的Q table，从而：
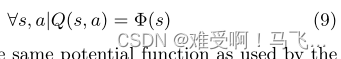
在这里插入图片描述
------其中 $Φ (\cdot)$ 是与塑形agent使用的势能函数相同的势能函数。

------然而，对于动态势能函数，这个结果不再成立。证明要求具有基于势能的奖励塑形的agent和具有上述 $Q$ 表初始化的agent在提供相同的状态、行动和奖励历史的情况下，在其下一个行动中具有相同的概率分布。

------如果在实验之前用状态的势能（ $Φ (s ， t^{'})$ ）初始化Q表，那么在初始化的试剂中不考虑势能的任何未来变化。因此，在agent经历了一种状态，其中塑形agent的势能函数发生了变化，他们可能会做出不同的后续行动选择。

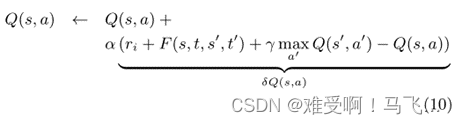
------形式上，这可以通过考虑接收基于动态势的奖励塑形的agent $L$ 和不接收但如等式9所示初始化的agent $L^′$ 来证明。Agent $L$ 将通过以下规则更新其Q值：
在这里插入图片描述
其中， $∆ Q (s, a) = α δ Q (s, a)$ 是 $Q$ 值更新的量。
Agent $L$ 的当前 $Q$ 值可以正式表示为初始值加上变化，因为：

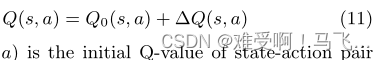
其中 $Q' (s ， a)$ 是状态-动作对 $(s ， a)$ 的初始 $Q$ 值。类似地，agent $L^′$ 通过以下规则更新其Q值：
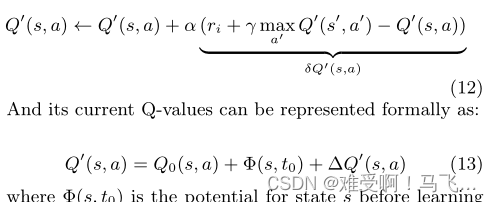
在这里插入图片描述
------其中 $Φ (s,t_0)$ 是学习开始前状态 $s$ 的势能。

------为了使两个agent行为相同，他们必须通过 $Q$ 值的相对差而不是绝对大小来选择其行为，并且两个agent的行为的相对顺序必须保持相同。正式地：
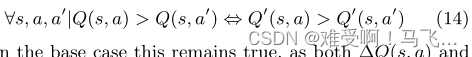
在这里插入图片描述
------在基本情况下，这仍然是正确的，因为 $∆ Q (s, a)$ 和 $∆$ 在采取任何行动之前， $Q^′(s,a)$ 等于零，但在这之后，动态势能函数的证明就不成立了。
------具体地，当agent首次转换到势能已改变的状态时，agent $L$ 将通过以下方式更新 $Q (s, a)$ ：
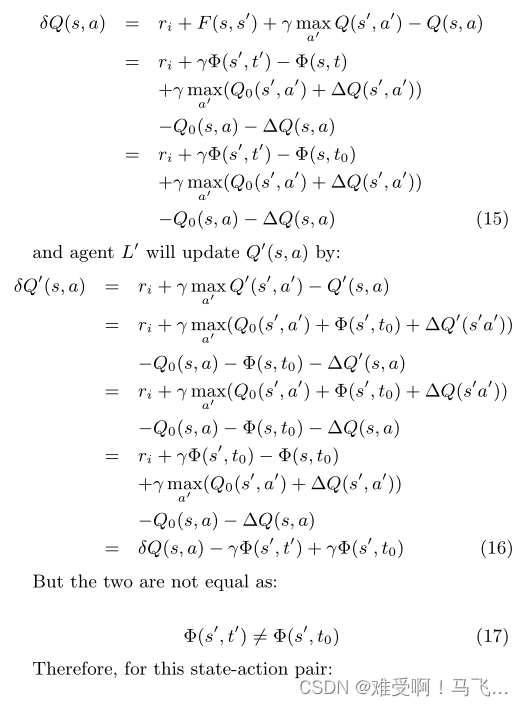
在这里插入图片描述

------一旦发生这种情况，状态s的agent L和agent L′之间的Q值差将不再在所有行动中保持恒定。如果这种差足以改变行动的顺序（即方程14被打破），那么任何理性agent的策略在状态s中的后续行动选择上都将具有不同的概率分布。