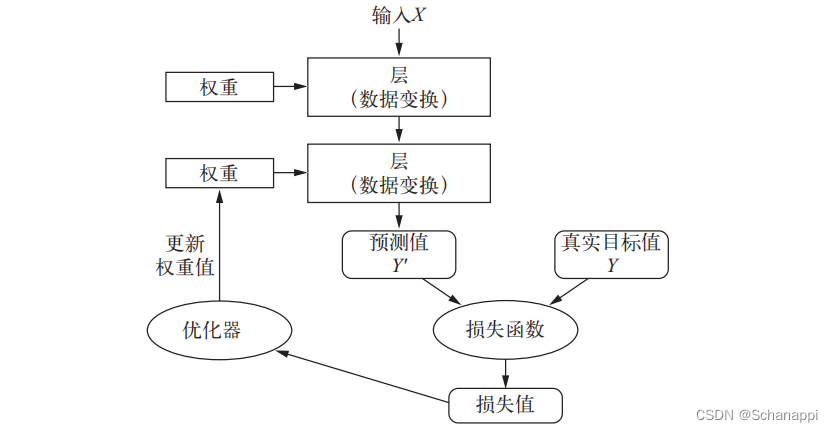
FP8训练调研
一、FP8训练相关技术要点总结
1、基于块的累加技术,减小低精度数之间相加的累积误差
2、随机舍入技术代替四舍五入,降低舍入误差
3、混合FP8技术,用1-4-3进行前向,1-5-2进行反向
4、设置指数偏移,使FP8表示数的范围能覆盖网络参数的范围
5、自动精度缩放,对网络中每层采用不同的缩放因子,减少上溢和下溢
6、修改1-4-3FP8表示方法,无法表达无穷,但把最大值从240扩展到448
7、采用有符号和无符号16位浮点数来存储参数
二、FP8训练各篇论文总结
(一)、Training Deep Neural Networks with 8-bit Floating Point Numbers
论文出处:这是IBM2018年发表的论文
1、论文所用新技术简述
(1)、提出分块累加的方法,当分层应用时,允许所有矩阵和卷积操作只使用8位乘法和16位加法计算。
(2)、在权值更新过程中应用浮点随机舍入,允许这些更新以16位的精度发生。
2、技术细节
2.1文中所述的8位浮点数(fp8)的(符号s、指数e、尾数m)格式为(1,5,2)位,即符号位s占1位,指数位e占5位,小数位m占2位,一个8位浮点数可以表示为:
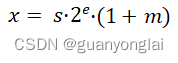
2.2分块累加:
把一个很长的点乘结果进行分块累加:首先设N是点乘后需要累加的数的个数,设CL为分块个数,那么理论上累加误差可以由O(N)缩小到O(N/CL + CL)
分块累加伪代码: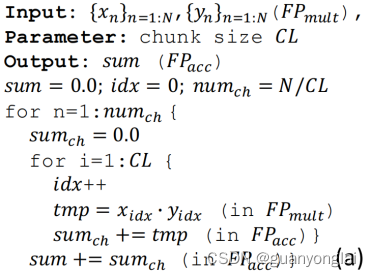
分块累加作用:防止一个教大的数和一个较少的数相加时,较小的数被淹没了,比如对于float16的两数相加 1025+0.1,结果并不是1025.1,而是1025,因为两个数的数量级差别太大,导致较小的数被舍弃了。
2.3随机舍入:
假设一个浮点数x表示为: 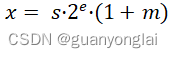
其中s、e、m分别为符号位、指数位、小数位。假设原来用较高精度表示m时,有k'位,现在需要把m用较低精度表示为[m],有k位,其中>=k,那么[m](类似L的符号打不出来,用[ ]代替)就是m的-k位最低有效位截断,可以理解为[m]就是m的近似值。X的随机舍入近似值可以表示为如下:
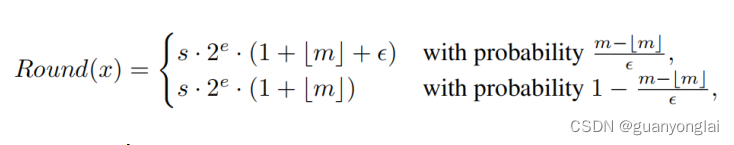
其中ε = ![]()
3、该技术的缺陷
随机舍入需要在关键计算路径中内置昂贵的随机舍入硬件,这不利于收缩阵列和GEMM加速器实现。
4、硬件平台
本文所讨论新思想的一个子集是在硬件中实现的,使用了基于14nm硅技术的基于数据流的新核心设计——结合了基于块的计算和训练中精度缩放的技术。
下图为基于FP16分块累加的新型数据流核心(14 nm)的芯片布局。FP8比FP16实现了2 ~ 4倍的效率提升,而且只需要更少的内存带宽和存储。
5、实验结果
5.1 不同计算单元的计算示意图
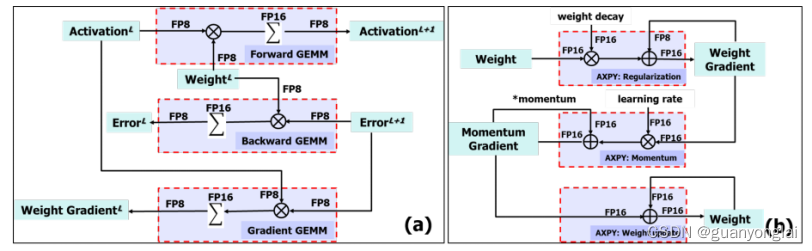
(a)三个GEMM模块的前向和反向示意图
(b)标准SGD优化器中权重更新过程中的三个AXPY运算
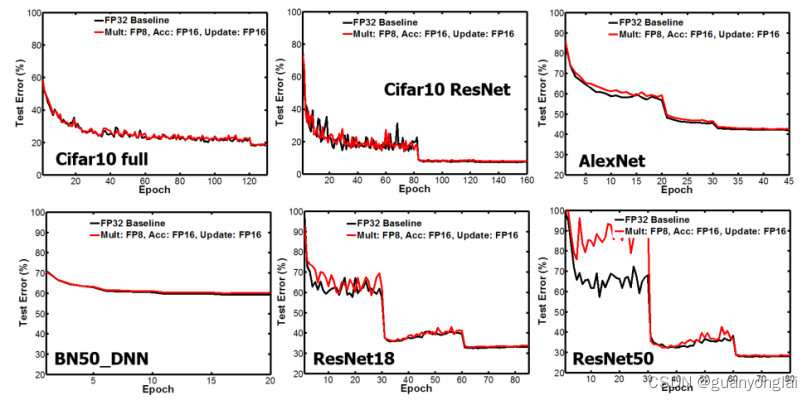
5.2 本文方法在使用分块数为64时,用FP8进行乘法计算、用FP16进行累加和梯度更新的实验结果,红线为实验组,黑线为单精度对照组。
(二)、Hybrid 8-bit Floating Point (HFP8) Training and Inference for Deep Neural Networks
论文出处:这是IBM2019年发表的论文
1、论文所用新技术简述
(1)、设计了一种新的混合FP8格式(HFP8),使用4个指数位和3个尾数位(带有指数偏置的1-4-3)进行正向传播,使用5个指数位和2个尾数位(1-5-2)进行反向传播。FC层使用FP16表示。
(2)、采用SoftMax最大值减法,在softmax中减去最大值之后再求e指数,这种精度下降可以完全消除。
(3)、介绍了一种确定性FP8权值更新方案,该方案可以收敛到FP32的精度,而无需使用随机舍入和兼容的AllReduce技术,该技术利用低位宽权值加快分布式学习。
2、技术细节
2.1因为前向的时候需要更高的精度,反向的时候梯度需要更大的表示范围,故采用带指数偏移的1-4-3格式的FP8进行前向,用1-5-2格式的FP8加自动调整系数的loss缩放来进行反向,所以叫混合FP8格式(HFP8)。
2.2 指数偏移
因为前向的过程中,数据的下溢问题更为严重,所以需要通过有限的8位表示更高的精度,故提出了指数偏移,加入指数偏移的(1-4-3)FP8的数据表示范围为:
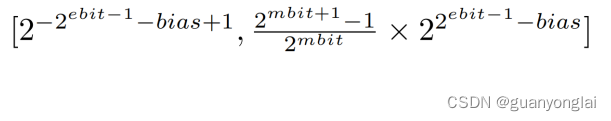
其中指数位ebit占4位,小数位mbit占3位,本文设置偏移量bias=4。则bias=4的FP8数据表示的精度和范围为[2^(-11), 30]。如果不用偏移bias,即bias=0,FP8的表示的精度和范围为[2^(-7),15/8 * 2^8],即 [2^(-7), 480]。所以在用了4位偏移之后,虽然使FP8表示的最大值从480降低到30,但是能够表示更小的激活和权重至2^(−11),远低于原来2^(−7)的精度,这正好解决了经常出现的数据下溢问题。偏移量为4的4位指数具有足够的范围和保真度来表示训练和跨精度推理性能的激活和权重。
2.3 SoftMax最大值减法
对于NLP这种最后一层FC层很大的网络,在FC层数据从16位转到8位的过程中,数据中的最大输出可能被量化为相同的值,因此在经过SoftMax层之后无法区分。所以把量化步骤放在SoftMax的最大值减法(如x-xmax)步骤之后执行,即在softmax中减去最大值之后再求e指数,这种精度下降可以完全消除。
3、实验结果
3.1 模型在不同精度下训练的loss平面如下图所示。上面一行是训练数据,下面一行是测试数据。由图可见,与FP32相比,HFP8的loss平面保持了良好的Lipschitz条件(利普希茨条件,是一个比通常连续更强的光滑性条件),而FP8的loss平面出现了多个鞍点,阻碍了训练收敛。
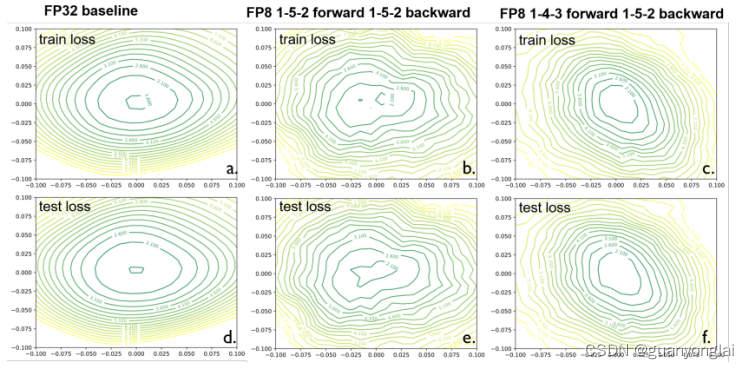
(a)FP32
(b)FP8 (所有GEMM计算模块都用1-5-2完成)
(c)HFP8 (前向用1-4-3,反向用1-5-2)
3.3 在不同模型上应用HFP8的训练曲线如下
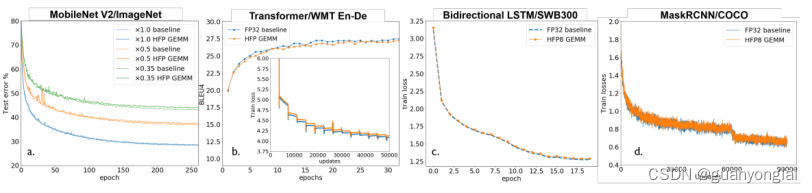
(a)具有不同宽度乘数的MobileNetV2
(b)基于Transformer的机器翻译
(c)基于LSTM的SWB300数据集语音模型
(d)Mask R-CNN 模型
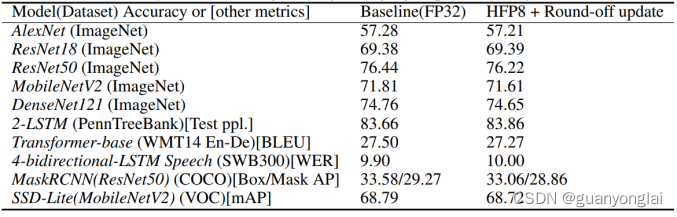
3.4 FP32与HFP8在各模型的训练结果:图像识别、自然语言、语音识别和目标检测模型
(三)、8-BIT NUMERICAL FORMATS FOR DEEP NEURAL NETWORKS
论文出处:这是一家英国人工智能芯片硬件设计初创公司Graphcore在2021年发表的论文
1、论文要点总结
本文主要讨论了浮点数相对于定点数表示的优势,在训练和推理中,对使用8位浮点数表示激活、权值和梯度进行了深入研究,探讨了不同位宽对指数、小数和指数偏移量的影响。
2、技术细节
2.1 位宽选择
证实在训练过程中采用1-4-3的FP8进行前向,用1-5-2的FP8进行反向这种方式是合理的。
2.2 指数偏移
在采用1-4-3和1-5-2的FP8表示形式时,都会进行一定的指数偏移,用以缓解数值溢出的问题。
2.3 自动loss缩放
一般会把loss缩放结合指数偏移一起做,文中有证明loss缩放2^22加上指数偏移15位,相当于指数偏移37位不做loss缩放。
自动loss缩放方法:首先给loss乘一个固定的缩放因子,如果有数值超过FP8表示的最大范围,就把缩放因子缩小2倍,接下来如果2000次迭代都没有再遇到超范围的情况,就再把缩放因子再增加2倍。
3、实验结果
3.1 给出了Transformer模型的复合直方图,以及本文使用的不同8位浮点数格式的动态范围。
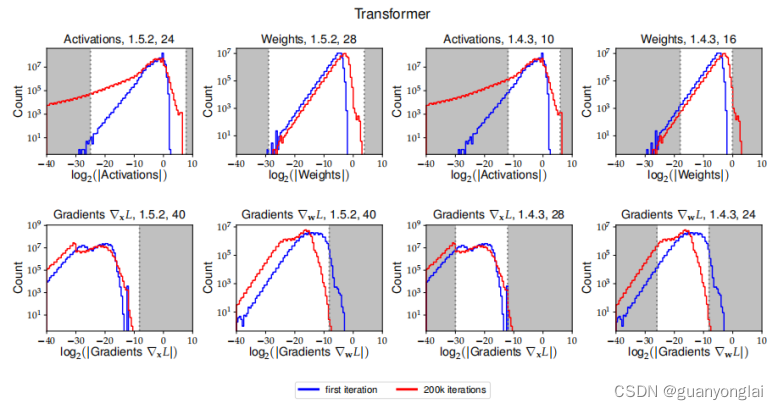
Transformer模型的权重、激活和梯度直方图WMT14 英语-德语翻译训练。白色区域对应于由各自的8位浮点数格式表示的值的范围。
(四)、Auto-Precision Scaling for Distributed Deep Learning
论文出处:这是乔治亚理工学院&美国美国加州大学伯克利分校&新加坡国立大学联合在2021年发表的论文
1、论文要点总结
(1)、本文提出了自动精确缩放(APS)算法。
(2)、APS可以在通信开销很小的情况下提高精度。
(3)、实验结果表明,在许多应用中,APS可以通过8位梯度训练业内最新的模型,没有或只有很小的精度损失(<0.05%),并获得明显加速。
2、技术细节
2.1首先论证了不同模型,或者相同模型不同层的梯度分布范围是不同的
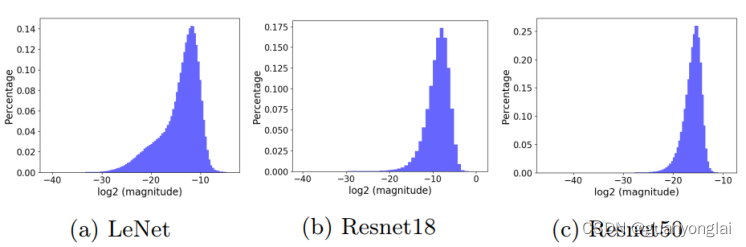
上三个子图分别统计了LeNet、Resnet18、Resnet50三个网络中梯度的分布范围
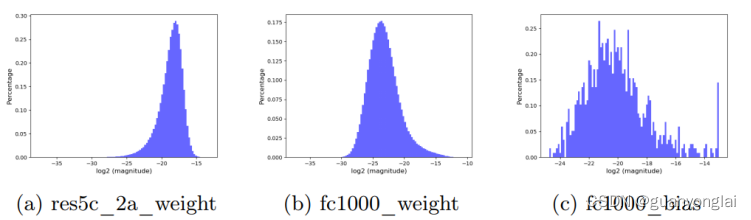
上图统计了Resnet50中不同层的梯度分布范围
2.2 自动精确缩放
因为不同模型的梯度分布范围不同,所以loss缩放是不可避免的。如下图a所示,假设两条竖黑线是FP8表示的下限和上限,蓝色和绿色曲线表示一个网络中两个不同层的梯度分布,可见如果直接用FP8表示,那么蓝色线会发生下溢,绿色先会上溢。如果用传统的loss缩放方法,即整个网络共用一个缩放因子,那么在选择缩放因子的时候,不管选择多大的缩放因子都会出现图b所示的现象,即不可避免会发生蓝色线下溢更严重或者绿色线上溢更严重的情况。所以本文提出不同层采用不同的缩放因子,这样就能使不同层的参数分布向不同的方向移动,使他们都能在FP8表示的范围之内,如下图c所示: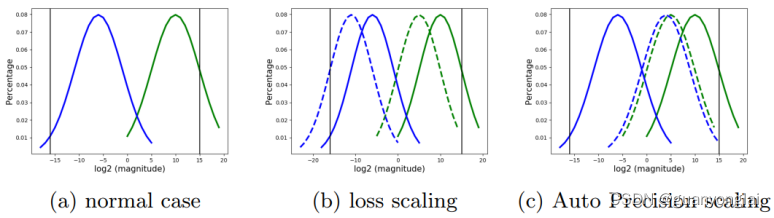
但即使这样,还是难以避免少数层同时发生上溢和下溢的情况,作者考虑到上溢会产生INF的无效数据,而INF数据同化能力很强,因为INF与别的数进行运算都会变成INF,所以本文选择缩放因子的原则是:在避免上溢的基础上尽量减少下溢,总结公式如下:
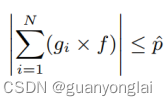
其中g表示梯度,f表示缩放因子,![]() 表示FP8的上限,N表示分布式系统中的节点数。
表示FP8的上限,N表示分布式系统中的节点数。
然而,对于一个分布式系统,每个节点只知道自己的梯度。而要解上面的优化问题,需要知道所有节点的梯度。本文使用启发式算法来寻找一个合适的比例因子。对上式放松了边界变为下面的公式:
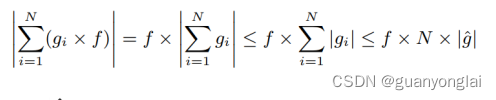
其中![]() 为一层中梯度的最大值。
为一层中梯度的最大值。
通过提出的启发式算法来得到一个次优解,即不再需要所有节点这一层的梯度信息,而只需要所有节点这一层的梯度的最大值。
3、实验结果
分类任务采用DavidNet and Resnet18模型,分割任务采用FCN模型,并在8卡的NVIDIA V100 GPU上训练,采用all-reduce的方式执行GPU之间的数据通信。分类模型采用的数据为CIFAR10,总batchsize设为4k,即每块卡512。在下表中总结了梯度精度与DavidNet/ResNet18准确率之间的关系:
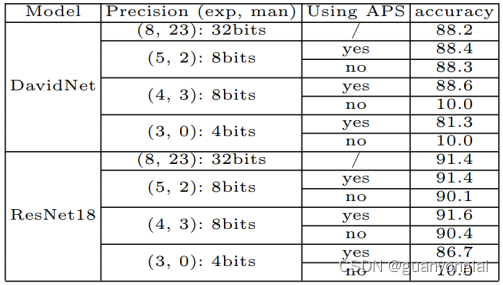
上表可以看到带APS的一组精度都比较高,即使4位数据训练也比基线只低两个点不到。
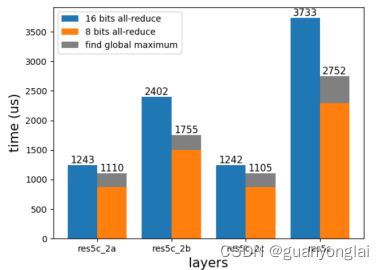
除了精度,本文还对比了性能:虽然APS可以支持用户用更低的精度训练,但是它引入了额外的通信和计算(解优化问题),所以需要确定它带来的好处是否大于额外开销。下图可以看到,在增加寻找每层最大值的计算量后,还是比原始的耗时要低,所以本文所提方法是可行的。
(五)、FP8 Formats For Deep Learning
论文出处:这是NVIDIA携手Intel和Arm于2022年发布的白皮书,希望能通过 8位浮点运算的格式来改善运算性能,并将其作为 AI 通用的交换格式,提升深度学习训练与推理速度。目前该白皮书也已提交给了电气与电子工程师协会(IEEE)
1、论文要点总结
本论文使用的新方法其实就是修改了普通1-4-3格式的FP8数的表示方法,使其不再符合IEEE754标准。但是本文使用的1-5-2格式的FP8数依然延用IEEE754标准。
2、技术细节
2.1 新的1-4-3格式的FP8数表示
本文依然采用1-4-3格式的FP8数进行前向,用1-5-2格式的FP8数进行反向。但是对1-4-3格式的FP8数表示方法做了一些调整。因为1-4-3数只有4位指数,如果按照IEEE754标准,其表示的最大数为1110.111,即2^(14-7)*(1/2+1/4+1/8)=240,表示范围太小了,所以需要通过修改表示方式来扩大表示范围。具体调整如下表所示:

上图右边E5M2的FP8浮点数是符合IEEE754规则的,可以看出左边E4M3的表示方式与其不同的地方有:E4M3无法表示无穷数,且E4M3只有一个小数位来表示NaN。从而也就导致了E4M3的最大值表示方法不同。
对于符合IEEE754标准的浮点数,当指数位全为1时,不管小数位是什么,一律都表示NaN或者无穷,但是这里的E4M3数只有在指数位全为1,且小数位也全为1时才表示NaN。也就是说当指数位全为1时,多了7种数值的表示方式,即小数位分别为:000、001、010、011、100、101、110。这七种情况表示的最大值分别为(256, 288, 320, 352, 384, 416, 448)。也就是说采用本文的E4M3表示方法,其最大表示范围可以从240扩展到448。
3、实验结果
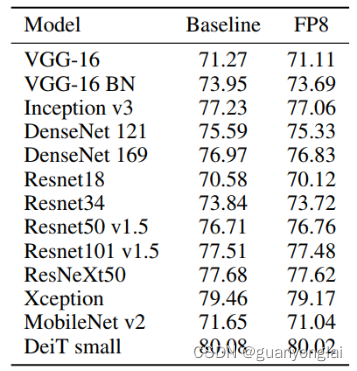
实验结果如下图所示,基线在FP16或者bfloat16下训练,而FP8组的所有GEMM计算单元的参数都用FP8格式表示,包括第一层卷积和最后一层全连接层。
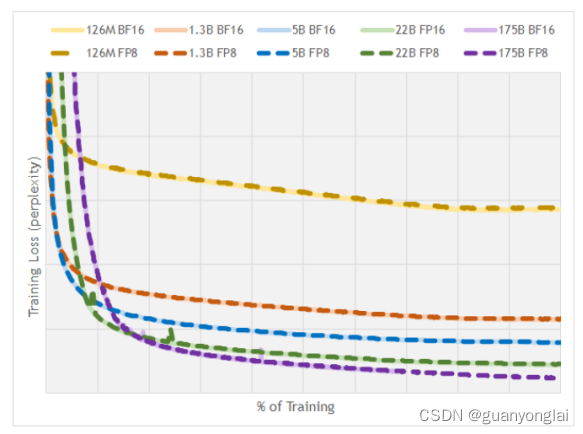
各种GPT-3模型的训练loss(perplexity)曲线如下图所示,其中x轴是归一化的迭代次数。
(六)、Mixed Precision Training With 8-bit Floating Point
论文出处:这是英特尔2019年发表的论文
1、论文所用新技术简述
(1)、提出了一种简单且可扩展的解决方案,用于构建FP8计算单元,消除了上面第一篇论文在关键计算路径中对随机舍入硬件的需求,从而降低了MAC单元的成本和复杂性。
(2)、提出了增强的loss缩放方法来补偿FP8表示的非规格数范围的减小,以改善误差传播,从而获得更好的模型精度。
(3)、详细研究了量化噪声对模型泛化的影响,提出了一种随机舍入技术来解决训练开始时的梯度噪声,从而更好地泛化。
2、技术细节
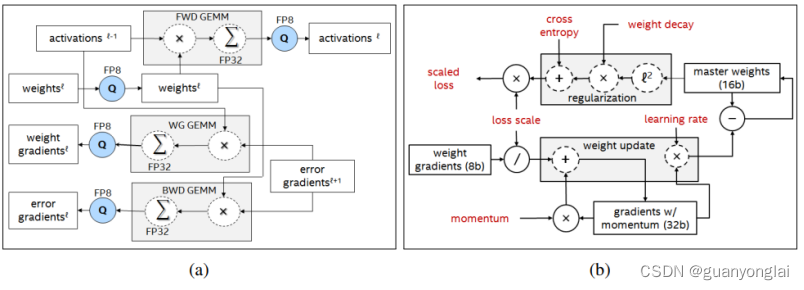
2.1 FP8训练的流程如下,左图为前向、反向和权重更新通道中关键计算内核的精度设置,右图为权重更新规则的流程图:
2.2 加强版的loss缩放
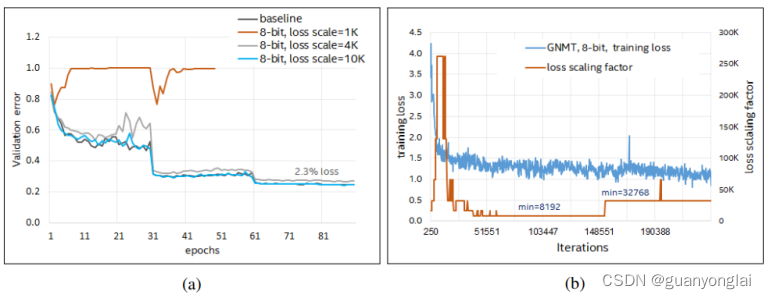
本文使用“back-off”动态loss缩放方法训练GNMT,该方法每隔几次迭代更新缩放因子。同时,为了弥补这种方法在处理FP8下溢方面的不足。对缩放因子更频繁更新的实验导致了loss收敛不稳定,从而可能引起loss发散。针对这一点,本文给出的方法是:通过观察训练过程中的损失函数来逐步增加缩放因子的“最小阈值”,即限定最小缩放因子。下图为使用增强loss缩放的FP8训练收敛过程。左图所示,Resnet-50在loss缩放因子为1000时未能收敛,在loss缩放因子为4000时表现较好,在loss缩放因子10000时表现完全收敛。右图显示随着缩放因子最小阈值逐渐增加的loss收敛过程,大约在40k次迭代的时候设置缩放因子最小值为8k,在150k次迭代的时候设置缩放因子最小值为32k。
2.3 随机舍入
与传统舍入技术不同,随机舍入技术使用输入中被丢弃的几个比特来计算舍入的概率,这样就不容易引入很大的舍入误差。本文所用随机舍入公式如下,其中x表示需要舍入的数,k表示目标精度,ε表示本文所用FP8的最小刻度,r表示由伪随机数发生器产生的随机值。

3、实验结果
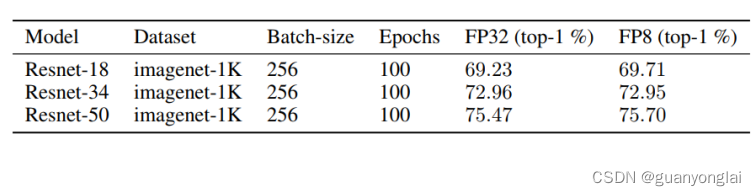
下表总结了卷积神经网络在imagenet-1K数据集上的验证精度。
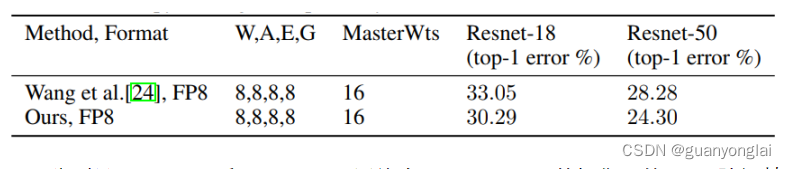
下表显示了在Imagenet-1K数据集上,本文方法与上面第一篇文章的FP8训练方法的比较。W、A、E、G、MasterWts分别表示权值、激活、误差、权值梯度和权值拷贝的精度设置。
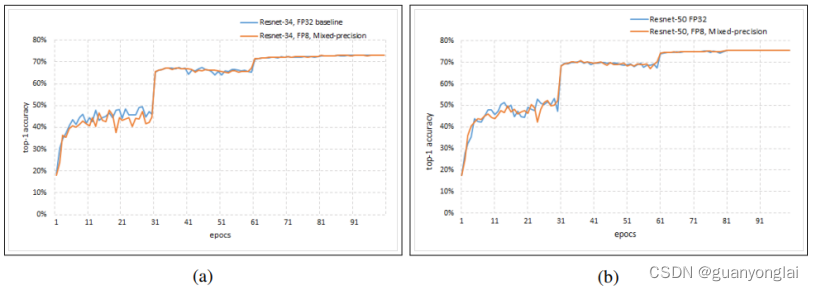
下图分别是Resnet-34和Resnet-50网络在imagenet-1K数据集上的top1验证精度。
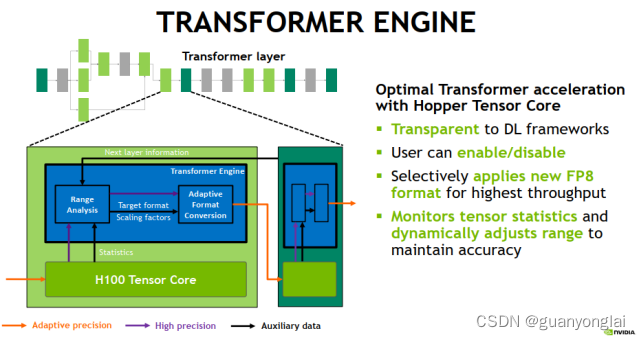
(七)、NVIDIA—H100—FP8混合精度训练
H100 TensorCore中引入了新的Format: FP8. 相较于FP16/BF16, 能得到2x的性能提升,和INT8的性能相当,并且支持Sparse的加速。
H100支持两种格式的FP8, FP8(1-4-3) 和 FP8(1-5-2),分别对应于不同的 Exponent 和 Mantissa 的比特数。两者所能表示的数值范围不同,比如 FP8(1-4-3) 多用于来表示 weights 和 activation,而 FP8(1-5-2) 来表示gradients。
H100中的累加器accumulator的精度可保持在FP16或者FP32上,经过bias和激活函数之后,再转换成希望得到的浮点类型,如FP8/FP16/BF16/FP32。支持多种FP类型的输出,提供了极大的灵活性。这样,上层软件 runtime/compiler就能够根据网络精度的要求,来灵活的选择哪些block可以运行在FP8,而那些对精度影响较大的block运行在FP16上面。
Nvidia公布的算法,能够自动监测数据的range,来决定最佳的FP8格式(1-4-3 or 1-5-2),在速度和精度上取得平衡。这里边可以做到对于DL framework来透明。
训练流程:

Range分析+自适应精度调整:
训练示例:

(八)、Tesla Dojo Technology --A Guide to Tesla’s Configurable Floating Point Formats & Arithmetic
论文出处:这是特斯拉2021年发表的白皮书
1、论文所用新技术简述
本标准引入了可配置的Float8 (CFloat8),符合本标准的浮点系统的实现可以完全在软件中实现,也可以完全在硬件中实现,或者在软硬件的任何组合中实现。
2、技术细节
因为权重、梯度、激活值具有不同的精度和动态范围要求,所以需要可配置FP8实现较高的训练精度。这种可配置性允许对指数位和尾数位的数量进行不同的分配,具体取决于所表示的参数。此外,这些参数的数值范围也有很大的差异。与激活值相比,权重和梯度通常小得多,所以需要使用可配置的指数偏置来满足各种参数的动态范围要求。在训练过程中,指数不会频繁变化,因此,在任何给定的执行步骤中只使用少量这样的指数偏差,并且在训练过程中可以学习到适当的指数偏置。
两种完全可配置指数偏置的CFloat8格式如下表所示:

CFloat8_1_4_3和CFloat8_1_5_2格式都支持规格化数、非规格化数和零。由于可表示的指数值数量有限,因此不支持无穷大和NaN编码。最大指数值并不用于编码NaN和无穷大,而是用于表示归一化浮点数。任何无穷大或NaN操作数,或者算术运算中的溢出操作数,都会将结果截断于可表示的最大数。
对于不同的指数偏置,CFloat8_1_4_3表示的数值范围为:
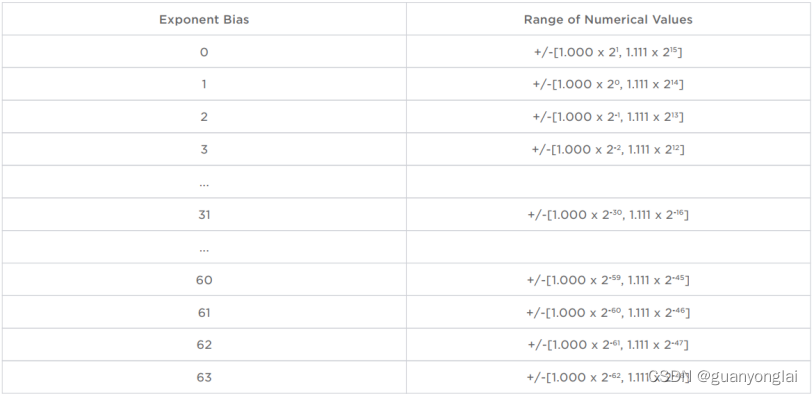
对于不同的指数偏置,CFloat8_1_5_2表示的数值范围为:
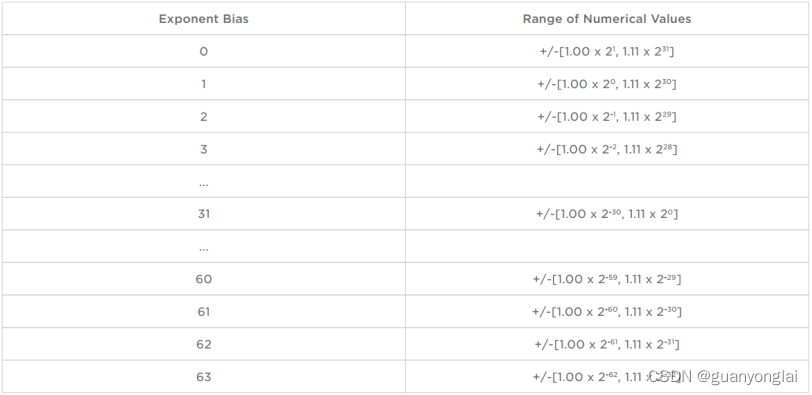
其中6位指数偏置用无符号整数表示,以牺牲较大的数值为代价,使可表示值的范围更多地倾斜于较小的数值,因为训练过程的参数一般会进行归一化,因此倾向于集中在非常小的数值。
要将BFloat16和IEEE Float32格式转换为CFLoat8的两种格式,还需支持四舍五入和随机舍入两种舍入模式。
同时本标准还提出两种半精度浮点数:有符号半精度(Signed Half Precision, SHP)和无符号半精度(Unsigned Half Precision, UHP),用于存储梯度等参数。两种格式的半精度浮点数配置如下:

SHP格式支持规格化数、非规格化数和零。不支持无穷和NaN编码。
UHP格式支持规格化数和零,也支持非规格化数,但是非规格化数会被刷新为零。UHP格式也支持无穷和NaN编码。




![刷题记录(NC20313 [SDOI2008]仪仗队)](https://img-blog.csdnimg.cn/25d26c6326444877827d3c1893ac427a.png)