【数据结构】图的遍历

news2024/10/6 1:45:58

深度优先遍历

深度优先遍历思想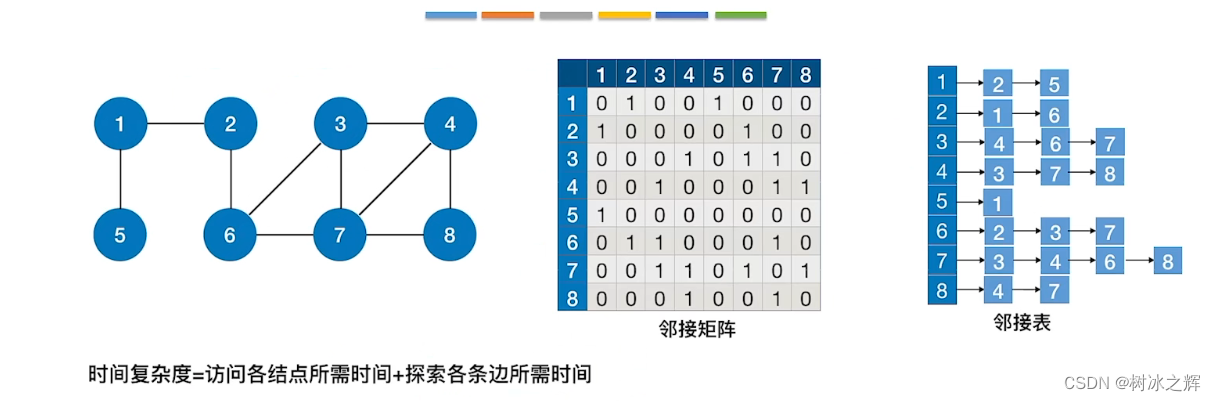

对于图：选中一个结点，访问和其相邻的、未被访问过的点，全部访问完毕后回退到上一个结点，直至全部结点访问完毕，类似于图的先序遍历，如有邻接表，则按邻接矩阵的顺序遍历。

时间复杂度：O(|v|)

对于邻接矩阵：选中一个结点，寻找其对应列标，找到后在此行依次从左向右遍历，如为1则对其行标的元素进行访问，然后寻找此元素的列标，与上一步进行循环，遇到访问过的结点则跳过，如一个列标行所有为1的结点访问完毕，则回溯到上一层。

时间复杂度：O(|v|²) 每行v，v行v²

对于邻接表：选中一个头结点，对其表结点从左向右进行访问，访问到第一个表结点后跳转到其对应的头结点，与上一步进行循环，如遇到访问过的结点则跳过，如一个头结点的表结点全部访问完毕则跳转至上一层头结点。

时间复杂度：O(|v|+|E|) 访问头结点：O(|v|) 访问头结点的邻接结点：O(|E|)

同一个图的邻接矩阵表示唯一，因此深度优先遍历序列唯一

同一个图的邻接表表示不唯一（表结点顺序可任意），因此深度优先遍历序列不唯一

深度优先遍历——伪代码

bool visited[MaxVertexNum] //存储访问状态的数组

void DFSTraverse(Graph G){
    int v;
    for(v=0;v<G.vexnum;++v) //遍历所有顶点
        visited[v]=FALSE; //将所有顶点初始化为未访问状态

    for(v=0;v<G.vexnum;++v) //遍历所有顶点
        if(!visited[v]) //找到第一个FALSE顶点
            DFS(G,v); //对其进行DFS遍历
}

void DFS(Graph G,int v) //递归遍历，顶点v、图G
{
    visit(v); //访问顶点v
    visited[v]=true; //将判断数组置为已访问

    for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))
    if(!visited[w]){
        DFS(G,w);
    } //if
}

广度优先遍历

广度优先遍历思想

对于图：选中一个结点，访问和其相邻的、未被访问过的所有的顶点，每个顶点分别呈辐射状向下遍历，相当于树的层次遍历

对于邻接表：选中一个结点，寻找其对应头结点，找到后在此行的所有表结点全部入队，并按照从左到右的顺序依次将表结点元素的对应头结点进行上一步操作，直至所有元素都被访问过

时间复杂度：O(|v|+|E|) 访问头结点：O(|v|) 访问头结点的邻接结点：O(|E|)

广度优先遍历——伪代码

总体思想：入队一个结点，将其出队并让其所有邻接结点入队，依次循环，直至队列为空

如果需要遍历的图G不是连通图，假设G有2个连通分量，BFSTraverse函数的第二个for循环会对每个连通分量都使用BFS来保证全部遍历完成，即找到第一个未访问结点后对其进行BFS直至整个连通分量都被遍历完毕，然后寻找下一个未被访问的结点，其所在连通分量必定都未被访问

bool visited[MaxVertexNum] //存储访问状态的数组

void BFSTraverse(Graph G){
    int i;
    for(i=0;i<G.vexnum;++i) //遍历所有顶点
        visited[i]=FALSE; //将所有顶点初始化为未访问状态
    InitQueue(Q); //初始化一个队列

    for(i=0;i<G.vexnum;++i) //遍历所有顶点、连通分量
        if(!visited[i]) //找到第一个顶点
            BFS(G,i); //对其进行BFS遍历，对每一个顶点都进行BFS
}

void BFS(Graph G,int v){//从顶点v出发

    visit(v);//访问顶点v
    visited[v]=TRUE;//将其置为已经访问
    Enqueue(Q,v);//将v入队

    while(!isEmpty(Q)){ //当队列为空停止循环
        DeQue(Q,v); //将v出队
        for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))//依次寻找v的所有邻接顶点w，每找到一个就循环一次
        if(!visited[w]){ //如果顶点w未被访问过
            visit(w); //访问顶点w
            visited[w]=TRUE; //将顶点w置为已访问
            EnQueue(Q,w); //将顶点w入队
        }//if
    }//while
}