✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
智能优化算法 神经网络预测 雷达通信 无线传感器
信号处理 图像处理 路径规划 元胞自动机 无人机 电力系统
⛄ 内容介绍
基于Matlab计算经典CFAR阈值
⛄ 完整代码
function T = calcCFARthreshold(nTest, nRef, thePFA)
% calculates classical radar CFAR threshold for 0-mean AWGN
% classical Neyman-Pearson detection threshold for radar detection
% under additive Gaussian white noise criterion and specifid false alarm
% probability.
% the threshold T is calculated such that under the noise-only condition
% 计算0均值AWGN的经典雷达CFAR阈值
% 雷达检测的经典Neyman-Pearson检测阈值
% 在加性高斯白噪声准则和特定的虚警概率下
% 仅在噪声条件下计算阈值T
% prob(Ptest > T * Pref) <= pfa Eq(1)公式1
%
% where Ptest is the sum of normed-squares of the nTest cells
% Pref is the sum of normed-squares of the nRef cells
% pfa is the required maximum type-I (aka false alarm prob) error
%其中:Ptest是nTest单元的标准平方和,Pref是nRef单元的标准平方和,pfa是所需的最大类型-I(又名虚警概率)误差
%
% inputs: nTest - the number of noise-only test cells
% nRef - the number of noise-only reference cells
% thePfA - maximum probability such that
% prob(Ptest/Pref > T) <= pfa Eq(2)
% This is equivalent to Eq(1)
%inputs:nTest - 仅噪声测试单元的数量
% nRef - 仅噪声参考单元的数量
% thePfA - 这样的最大概率prob(Ptest / Pref> T)<= pfa Eq(2)相当于方程(1)
% demo: calcCFARthreshold; % no inputs
%demo: 计算0均值AWGN的经典雷达CFAR阈值;%无输入
% the classical CFAR processor compares the total power in nTest cells
% to the power in nRef cells. The threshold T is selected so that the
% ratio of Eq(2) is satisfied. it is assumed that the both sets' cells
% contain only thermal (AWGN) noise. If this ratio exceeds T, it assumed a
% radar target exists. The probability that only noise exceeds T is given
% by the threshold T (usually on the order of 10^-4 to 10^-7).
%经典CFAR处理器将nTest单元中的总功率与nRef单元中的功率进行比较。
%选择阈值T使得满足Eq(2)(公式2)的比率。
%假设两组'单元仅包含热(AWGN)噪声。
%如果该比率超过T,则假定存在雷达目标。
%仅噪声超过T的概率由阈值T给出(通常在10 ^ -4到10 ^ -7的数量级)。
% michaelB brost. as usual, fully sharable under GPLv3
% michaelB brost. 像往常一样,在GPLv3下完全可以共享
% demo
if(nargin == 0),%nargin是用来判断输入变量个数的函数:如果输入变量的数目为0
nTest = 10; %仅噪声测试单元个数
nRef = 25; %仅噪声参考单元的数量
thePFA = 1e-4;%方程2:“prob(Ptest/Pref > T) <= pfa”的最大概率,方程2等效与方程1“prob(Ptest > T * Pref) <= pfa”
T = calcCFARthreshold(nTest, nRef, thePFA);
doTest(nTest, nRef, thePFA, T);
clear('T');
return;
end
% requires the statistics toolbox需要统计工具箱
T = finv(1 - thePFA, nTest, nRef) * nTest / nRef;
return
function doTest(nTest, nRef, thePfa, T)
% simple test of threshold calc阈值计算的简单测试
nPt = min(1e5, ceil(50/thePfa));
nIter = 15;
nHit = zeros(nIter, 1);
wHnd = waitbar(0, '');
for k1=1:nIter
% test set noise power测试设置噪声功率
testPower = sum(randn(nPt, nTest).^2, 2);
% reference set noise power参考设定噪声功率
refPower = sum(randn(nPt, nRef).^2, 2);
% test
index = find(testPower >= (T .* refPower));
% >(大于),>=(大于等于),<(小于),<=(小于等于), ==(等于),~=(不等于)
% count up contacts 计数
nHit(k1) = length(index);
waitbar(k1/nIter, wHnd, sprintf('PFA simulation iteration %d of %d', k1, nIter));
end
close(wHnd);
pHit = nHit / nPt;
figure;
stem(pHit);
ylabel('P_F_A');
xlabel('runs');
pfaAvg = mean(pHit);
pfaStd = sqrt(var(pHit));
title(sprintf(...
'calculated average pfa: %5.3e, 1-sigma: %5.3e (design: %5.2e)\n', ...
pfaAvg, pfaStd, thePfa));
hold on;
lHnd = line([1, nIter], [thePfa, thePfa]);
set(lHnd, 'color', 'k');
lHnd = line([1, nIter], [pfaAvg, pfaAvg]);
set(lHnd, 'color', 'b');
lHnd = line([1, nIter], [thePfa, thePfa] - pfaStd);
set(lHnd, 'color', 'r');
lHnd = line([1, nIter], [thePfa, thePfa] + pfaStd);
set(lHnd, 'color', 'r');
legend('simulated PFA', 'specified PFA', 'mean PFA', '1 \sigma limits', ...
'location', 'south');
set(gca, 'xlim', [0, nIter+1]);
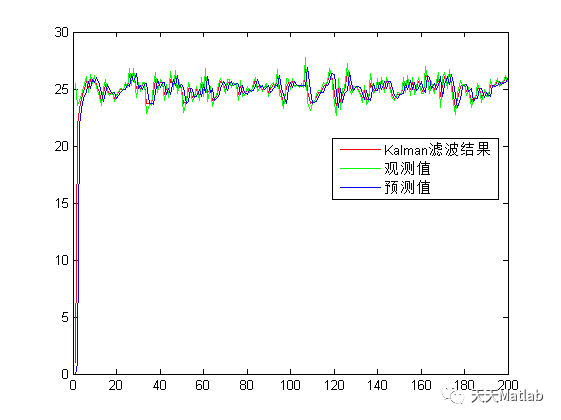
⛄ 运行结果
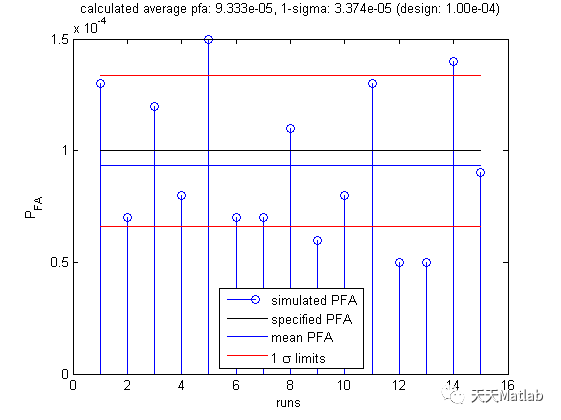
⛄ 参考文献
⛄ Matlab代码关注
❤️部分理论引用网络文献,若有侵权联系博主删除
❤️ 关注我领取海量matlab电子书和数学建模资料