优化器scipy.optimize参考指南

原文：https://mp.weixin.qq.com/s/BDHXQHXSzDk-RTi-VNMNEw

1 scipy.optimize简介

该scipy.optimize包提供几种常用的优化算法。

该模块包含：

1、使用多种算法（例如BFGS，Nelder-Mead单形，牛顿共轭梯度，COBYLA或SLSQP）对多元标量函数进行无约束和无约束的最小化（最小化）

2、全局（强力）优化例程（例如，盆地跳动，differential_evolution）

3、最小二乘最小化（least_squares）和曲线拟合（curve_fit）算法

4、标量单变量函数最小化器（minimum_scalar）和根查找器（牛顿）

5、使用多种算法（例如，混合鲍威尔，莱文贝格-马夸特或大型方法，例如牛顿-克里洛夫）的多元方程组求解器（root）。

详见：

https://docs.scipy.org/doc/scipy/reference/optimize.html

# https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html

from scipy.optimize import minimize

scipy.optimize.minimize(
					   fun,  #可调用的目标函数。
                       x0,  #ndarray,初值。（n,）
                       args=(), #额外的参数传递给目标函数及其导数
                       method=None, #类型的解算器。应该是其中之一:
									#‘Nelder-Mead’、‘Powell’
									#‘CG’、‘BFGS’
									#‘Newton-CG’、‘L-BFGS-B’ 
									#‘TNC’、‘COBYLA’
									#‘SLSQP’、‘dogleg’ 
									#‘trust-ncg’ 

                       jac=None, #目标函数的雅可比矩阵(梯度向量)。
                                 #仅适用于CG, BFGS, Newton-CG, 
                                 #L-BFGS-B, TNC, SLSQP, dogleg，
                                 #trust-ncg。如果jac是一个布尔值，
                                 #且为True，则假定fun将随目标函数返回
                                 #梯度。如果为False，则用数值方法估计梯
                                 #度。Jac也可以是返回目标梯度的可调用对
                                 #象。在这种情况下，它必须接受与乐趣相同
                                 #的论点。
                       hess=None, 
                       hessp=None,#目标函数的Hessian(二阶导数矩阵)或
                                  #目标函数的Hessian乘以任意向量p。
                                  #仅适用于Newton-CG, dogleg,
                                  #trust-ncg。只需要给出一个hessp或
                                  #hess。如果提供了hess，则将忽略
                                  #hessp。如果不提供hess和hessp，则用
                                  #jac上的有限差分来近似Hessian积。
                                  #hessp必须计算Hessian乘以任意向量。
               
                       bounds=None, #变量的边界(仅适用于L-BFGS-B, 
                                    #TNC和SLSQP)。(min, max)
                                    #对x中的每个元素，定义该参数的
                                    #边界。当在min或max方向上没有边界
                                    #时，使用None表示其中之一。
                       constraints=(), #约束定义
                       				   #(仅适用于COBYLA和SLSQP)
                       				   # 类型有: ‘eq’ for equality, ‘ineq’ for inequality
                       tol=None, #终止的边界。
                       callback=None, 
                       options=None)

返回值: res : OptimizeResult
#以OptimizeResult对象表示的优化结果。重要的属性有:x是解决方案数组，
#success是一个布尔标志，指示优化器是否成功退出，以及描述终止原因的消息。

2 无约束最小化多元标量函数

2.1 单纯形法:Nelder-Mead

函数Rosenbrock ：

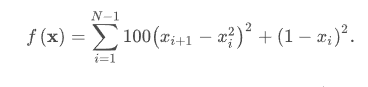
x=1时，取最小值。

def rosen(x):
    """The Rosenbrock function"""
    return sum(100.0 * (x[1:] - x[:-1] ** 2.0) ** 2.0 + (1 - x[:-1]) ** 2.0)

求解：

import numpy as np
from scipy.optimize import minimize

# 初始迭代点
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
 
# 最小化优化器，方法：Nelder-Mead（单纯形法）
res = minimize(rosen, x0, method='nelder-mead',
               options={'xatol': 1e-8, 'disp': True})
 
print(res.x)
 
#
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 339
         Function evaluations: 571
[1. 1. 1. 1. 1.]

求带有参数的 Rosenbrock 函数：

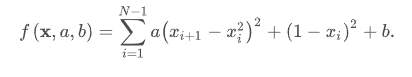
def rosen_with_args(x, a, b):
    """The Rosenbrock function with additional arguments"""
    return sum(a*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0) + b
    
res = minimize(rosen_with_args, x0, method='nelder-mead',
               args=(0.5, 1.), options={'xatol': 1e-8, 'disp': True})

2.2 拟牛顿法:BFGS算法

介绍：

https://blog.csdn.net/jiang425776024/article/details/87602847

Rosenbrock导数：

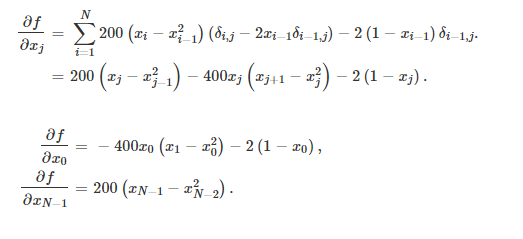
def rosen_der(x):
    # rosen函数的雅可比矩阵
    xm = x[1:-1]
    xm_m1 = x[:-2]
    xm_p1 = x[2:]
    der = np.zeros_like(x)
    der[1:-1] = 200 * (xm - xm_m1 ** 2) - 400 * (xm_p1 - xm ** 2) * xm - 2 * (1 - xm)
    der[0] = -400 * x[0] * (x[1] - x[0] ** 2) - 2 * (1 - x[0])
    der[-1] = 200 * (x[-1] - x[-2] ** 2)
    return der

求解：

# 初始迭代点
res = minimize(rosen, x0, method='BFGS', jac=rosen_der,
               options={'disp': True}) 
print(res.x)

提供梯度信息的另一种方法是编写一个返回目标和梯度的函数:这可以通过设置jac=True来表示。在这种情况下，要优化的Python函数必须返回一个元组，其第一个值是目标，第二个值表示梯度。

def rosen_and_der(x):
    objective = sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0)
    xm = x[1:-1]
    xm_m1 = x[:-2]
    xm_p1 = x[2:]
    der = np.zeros_like(x)
    der[1:-1] = 200*(xm-xm_m1**2) - 400*(xm_p1 - xm**2)*xm - 2*(1-xm)
    der[0] = -400*x[0]*(x[1]-x[0]**2) - 2*(1-x[0])
    der[-1] = 200*(x[-1]-x[-2]**2)
    return objective, der

res = minimize(rosen_and_der, x0, method='BFGS', jac=True,
               options={'disp': True})

2.3 牛顿法:Newton-CG

利用黑塞矩阵和梯度来优化。

介绍：

https://blog.csdn.net/jiang425776024/article/details/87602847

构造目标函数的近似二次型（泰勒展开）：

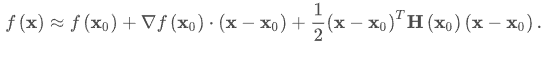
利用黑塞矩阵H和梯度做迭代：

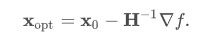
黑塞矩阵：

def rosen_hess(x):
    x = np.asarray(x)
    H = np.diag(-400*x[:-1],1) - np.diag(400*x[:-1],-1)
    diagonal = np.zeros_like(x)
    diagonal[0] = 1200*x[0]**2-400*x[1]+2
    diagonal[-1] = 200
    diagonal[1:-1] = 202 + 1200*x[1:-1]**2 - 400*x[2:]
    H = H + np.diag(diagonal)
    return H

res = minimize(rosen, x0, method='Newton-CG',
               jac=rosen_der, hess=rosen_hess,
               options={'xtol': 1e-8, 'disp': True})
res.x
# array([1.,  1.,  1.,  1.,  1.])

对于较大的最小化问题，存储整个Hessian矩阵会消耗大量的时间和内存。可将矩阵写成目标函数的形式：

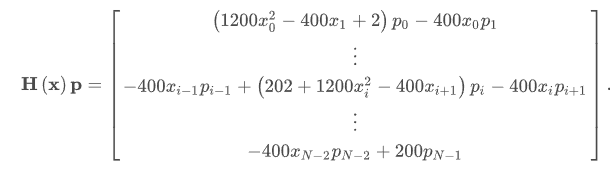
def rosen_hess_p(x, p):
    x = np.asarray(x)
    Hp = np.zeros_like(x)
    Hp[0] = (1200*x[0]**2 - 400*x[1] + 2)*p[0] - 400*x[0]*p[1]
    Hp[1:-1] = -400*x[:-2]*p[:-2]+(202+1200*x[1:-1]**2-400*x[2:])*p[1:-1] \
               -400*x[1:-1]*p[2:]
    Hp[-1] = -400*x[-2]*p[-2] + 200*p[-1]
    return Hp

res = minimize(rosen, x0, method='Newton-CG',
               jac=rosen_der, hessp=rosen_hess_p,
               options={'xtol': 1e-8, 'disp': True})

res.x
# array([1., 1., 1., 1., 1.])

当Hessian条件不佳时，Newton-CG算法可能是低效的，因为在这些情况下，该方法提供的搜索方向质量很差。trust-ncg方法可以更有效地处理这种有问题的情况，下面将对此进行描述。

2.4 共轭梯度算法:trust-krylov

与trust-ncg方法类似，trust-krylov方法是一种适用于大规模问题的方法，因为它只使用hessian作为线性算子，通过矩阵-向量乘积。它比trust-ncg方法更准确地解决了二次子问题。

Newton-CG方法是一种直线搜索方法：它找到一个搜索方向，使函数的二次逼近最小化，然后使用直线搜索算法找到该方向(接近)的最佳步长。另一种方法是，首先固定步长限制，然后通过求解以下二次问题在给定信任半径内找到最优步长：

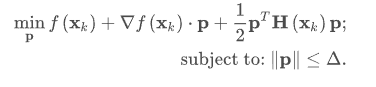
根据二次模型与实函数的一致程度，更新解 $x_{k+1}=x_k+p$ ，调整信任半径 $\Delta$ 。这类方法称为信任域方法(trust-region methods)。trust-ncg算法是一种利用共轭梯度算法求解信任域子问题的信任域方法。

# Full Hessian example
res = minimize(rosen, x0, method='trust-ncg',
               jac=rosen_der, hess=rosen_hess,
               options={'gtol': 1e-8, 'disp': True})

# Hessian product example
res = minimize(rosen, x0, method='trust-ncg',
               jac=rosen_der, hessp=rosen_hess_p,
               options={'gtol': 1e-8, 'disp': True})

3 约束最小化多元标量函数

最小化函数提供了约束最小化算法，即’trust-constr’， ‘SLSQP’和’COBYLA’。它们要求使用稍微不同的结构来定义约束。

方法’trust-constr’要求将约束定义为线性约束和非线性约束对象的序列。

另一方面，方法’SLSQP’和’COBYLA’要求将约束定义为一个字典序列，包含键type、fun和jac。

3.1 信任域:trust-constr

信任域约束方法处理的约束最小化问题形式为:

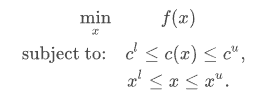
定义约束的边界：

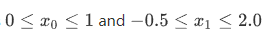
from scipy.optimize import Bounds
bounds = Bounds([0, -0.5], [1.0, 2.0])

定义线性约束

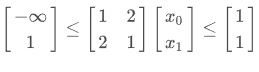
from scipy.optimize import LinearConstraint
linear_constraint = LinearConstraint([[1, 2], [2, 1]], [-np.inf, 1], [1, 1])

定义非线性约束

def cons_f(x):
    return [x[0]**2 + x[1], x[0]**2 - x[1]]
def cons_J(x):
    return [[2*x[0], 1], [2*x[0], -1]]
def cons_H(x, v):
    return v[0]*np.array([[2, 0], [0, 0]]) + v[1]*np.array([[2, 0], [0, 0]])
from scipy.optimize import NonlinearConstraint
nonlinear_constraint = NonlinearConstraint(cons_f, -np.inf, 1, jac=cons_J, hess=cons_H)

x0 = np.array([0.5, 0])
res = minimize(rosen, x0, method='trust-constr', jac=rosen_der, hess=rosen_hess,
               constraints=[linear_constraint, nonlinear_constraint],
               options={'verbose': 1}, bounds=bounds)

# may vary
# `gtol` termination condition is satisfied.
# Number of iterations: 12, function evaluations: 8, CG iterations: 7, 
# optimality: 2.99e-09, constraint violation: 1.11e-16, execution time: 
# 0.016 s.

print(res.x)

# [0.41494531 0.17010937]

3.2 顺序最小二乘规划算法:SLSQP

约束形式：

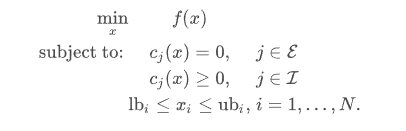
ineq_cons = {'type': 'ineq',
             'fun' : lambda x: np.array([1 - x[0] - 2*x[1],
                                         1 - x[0]**2 - x[1],
                                         1 - x[0]**2 + x[1]]),
             'jac' : lambda x: np.array([[-1.0, -2.0],
                                         [-2*x[0], -1.0],
                                         [-2*x[0], 1.0]])}
eq_cons = {'type': 'eq',
           'fun' : lambda x: np.array([2*x[0] + x[1] - 1]),
           'jac' : lambda x: np.array([2.0, 1.0])}

注意这里的不等式是≥0，与pymoo(≤0)相反。

x0 = np.array([0.5, 0])
res = minimize(rosen, x0, method='SLSQP', jac=rosen_der,
               constraints=[eq_cons, ineq_cons], options={'ftol': 1e-9, 'disp': True},
               bounds=bounds)
# may vary
Optimization terminated successfully.    (Exit mode 0)
            Current function value: 0.342717574857755
            Iterations: 5
            Function evaluations: 6
            Gradient evaluations: 5
print(res.x)
# [0.41494475 0.1701105 ]

3.3 最小二乘:least_squares

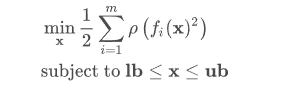
这里的f表示损失函数。

假设其为：

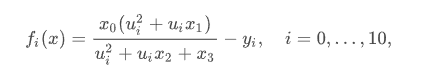
其导数：

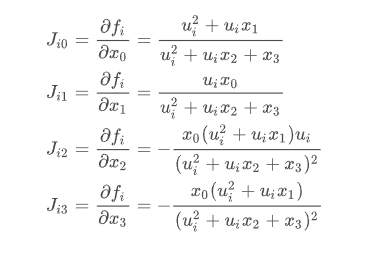
约束：

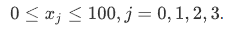
from scipy.optimize import least_squares

def model(x, u):
    return x[0] * (u ** 2 + x[1] * u) / (u ** 2 + x[2] * u + x[3])

def fun(x, u, y):
    return model(x, u) - y

def jac(x, u, y):
    J = np.empty((u.size, x.size))
    den = u ** 2 + x[2] * u + x[3]
    num = u ** 2 + x[1] * u
    J[:, 0] = num / den
    J[:, 1] = x[0] * u / den
    J[:, 2] = -x[0] * num * u / den ** 2
    J[:, 3] = -x[0] * num / den ** 2
    return J

u = np.array([4.0, 2.0, 1.0, 5.0e-1, 2.5e-1, 1.67e-1, 1.25e-1, 1.0e-1,
              8.33e-2, 7.14e-2, 6.25e-2])
y = np.array([1.957e-1, 1.947e-1, 1.735e-1, 1.6e-1, 8.44e-2, 6.27e-2,
              4.56e-2, 3.42e-2, 3.23e-2, 2.35e-2, 2.46e-2])
x0 = np.array([2.5, 3.9, 4.15, 3.9])
res = least_squares(fun, x0, jac=jac, bounds=(0, 100), args=(u, y), verbose=1)
# may vary
`ftol` termination condition is satisfied.
Function evaluations 130, initial cost 4.4383e+00, final cost 1.5375e-04, first-order optimality 4.92e-08.

res.x
# array([ 0.19280596,  0.19130423,  0.12306063,  0.13607247])

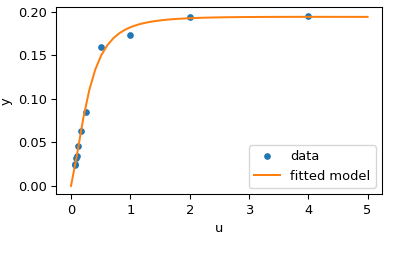
import matplotlib.pyplot as plt
u_test = np.linspace(0, 5)
y_test = model(res.x, u_test)
plt.plot(u, y, 'o', markersize=4, label='data')
plt.plot(u_test, y_test, label='fitted model')
plt.xlabel("u")
plt.ylabel("y")
plt.legend(loc='lower right')
plt.show()

4 单变量函数最小化器

from scipy.optimize import minimize_scalar
f = lambda x: (x - 2) * (x + 1)**2
res = minimize_scalar(f, method='brent')
print(res.x)
# 1.0

5 有界最小化

from scipy.special import j1
res = minimize_scalar(j1, bounds=(4, 7), method='bounded')
res.x
# 5.33144184241

6 自定义最小化器

from scipy.optimize import OptimizeResult
def custmin(fun, x0, args=(), maxfev=None, stepsize=0.1,
        maxiter=100, callback=None, **options):
    bestx = x0
    besty = fun(x0)
    funcalls = 1
    niter = 0
    improved = True
    stop = False

    while improved and not stop and niter < maxiter:
        improved = False
        niter += 1
        for dim in range(np.size(x0)):
            for s in [bestx[dim] - stepsize, bestx[dim] + stepsize]:
                testx = np.copy(bestx)
                testx[dim] = s
                testy = fun(testx, *args)
                funcalls += 1
                if testy < besty:
                    besty = testy
                    bestx = testx
                    improved = True
            if callback is not None:
                callback(bestx)
            if maxfev is not None and funcalls >= maxfev:
                stop = True
                break

    return OptimizeResult(fun=besty, x=bestx, nit=niter,
                          nfev=funcalls, success=(niter > 1))

x0 = [1.35, 0.9, 0.8, 1.1, 1.2]
res = minimize(rosen, x0, method=custmin, options=dict(stepsize=0.05))

res.x
# array([1., 1., 1., 1., 1.])

7 找根

单变量

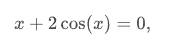
from scipy.optimize import root

def func(x):
    return x + 2 * np.cos(x)

sol = root(func, 0.3)

sol.x
# array([-1.02986653])

sol.fun
# array([ -6.66133815e-16])

多变量

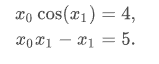
def func2(x):
    f = [x[0] * np.cos(x[1]) - 4,
         x[1]*x[0] - x[1] - 5]
    df = np.array([[np.cos(x[1]), -x[0] * np.sin(x[1])],
                   [x[1], x[0] - 1]])
    return f, df

sol = root(func2, [1, 1], jac=True, method='lm')

sol.x
# array([ 6.50409711,  0.90841421])

8 线性规划

问题：

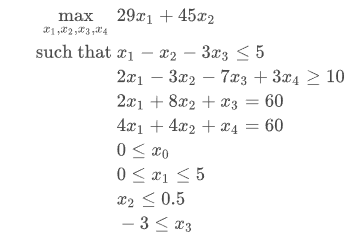
上述是最大小，需要转换成最小化，才可使用求解器linprog。

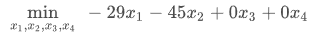
定义 x：

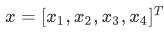
则目标函数的系数为：

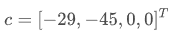
考虑两个不等式约束条件。

第一个是“小于”不等式，所以它已经是linprog所接受的形式。第二个是“大于”不等式，所以需要在两边同时乘以-1，将其转化为“小于”不等式。

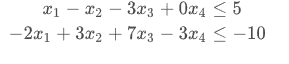
准换成矩阵形式：

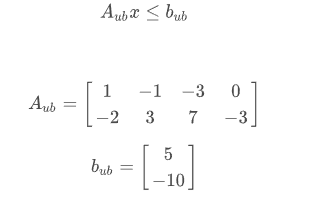
考虑两个等式：

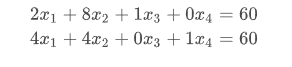
矩阵形式：

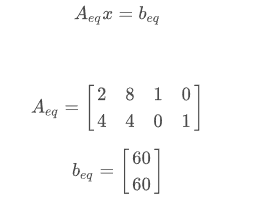
from scipy.optimize import linprog

c = np.array([-29.0, -45.0, 0.0, 0.0])

A_ub = np.array([[1.0, -1.0, -3.0, 0.0],
                [-2.0, 3.0, 7.0, -3.0]])
b_ub = np.array([5.0, -10.0])

A_eq = np.array([[2.0, 8.0, 1.0, 0.0],
                [4.0, 4.0, 0.0, 1.0]])
b_eq = np.array([60.0, 60.0])

x0_bounds = (0, None)
x1_bounds = (0, 5.0)
x2_bounds = (-np.inf, 0.5)  # +/- np.inf can be used instead of None
x3_bounds = (-3.0, None)

bounds = [x0_bounds, x1_bounds, x2_bounds, x3_bounds]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds)

print(result)

     con: array([15.5361242 , 16.61288005])  # may vary
     fun: -370.2321976308326  # may vary
 message: 'The algorithm terminated successfully and determined that the problem is infeasible.'
     nit: 6  # may vary
   slack: array([ 0.79314989, -1.76308532])  # may vary
  status: 2
 success: False
       x: array([ 6.60059391,  3.97366609, -0.52664076,  1.09007993])  # may vary

结果表明问题是不可行的，这意味着不存在满足所有约束条件的解向量。

这并不一定意味着做错。有些问题确实是行不通的。

假设约束太紧了，可以放松。调整代码x1_bounds =(0,6)：

x1_bounds = (0, 6)
bounds = [x0_bounds, x1_bounds, x2_bounds, x3_bounds]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds)

print(result)

    con: array([9.78840831e-09, 1.04662945e-08])  # may vary
    fun: -505.97435889013434  # may vary
message: 'Optimization terminated successfully.'
    nit: 4  # may vary
  slack: array([ 6.52747190e-10, -2.26730279e-09])  # may vary
 status: 0
success: True
      x: array([ 9.41025641,  5.17948718, -0.25641026,  1.64102564])  # may vary

x = np.array(result.x)

print(c @ x)
# -505.97435889013434  # may vary

9 指派问题

考虑到为游泳混合泳接力队挑选学生的问题。我们有一个表格，列出了五个学生每种泳姿的时间：

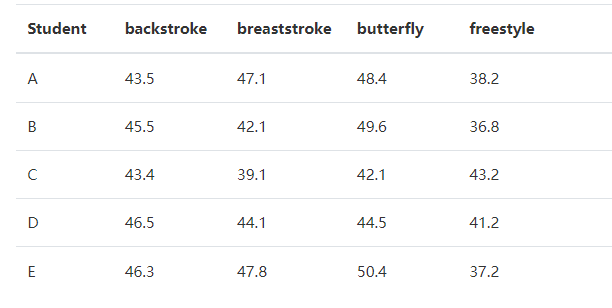
解决方案：定义一个成本矩阵C，每行只有一列有值，矩阵和为最终成本

定义目标函数：

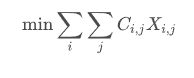
X是一个二值矩阵，当行i被指定到列j时， $X_{ij}=1$ 。

cost = np.array([[43.5, 45.5, 43.4, 46.5, 46.3],
                 [47.1, 42.1, 39.1, 44.1, 47.8],
                 [48.4, 49.6, 42.1, 44.5, 50.4],
                 [38.2, 36.8, 43.2, 41.2, 37.2]])

from scipy.optimize import linear_sum_assignment
row_ind, col_ind = linear_sum_assignment(cost) # 行索引，列索引

row_ind
# array([0, 1, 2, 3])
col_ind
# array([0, 2, 3, 1])

# 最优分配
styles = np.array(["backstroke", "breaststroke", "butterfly", "freestyle"])[row_ind]
students = np.array(["A", "B", "C", "D", "E"])[col_ind]
dict(zip(styles, students))
{'backstroke': 'A', 'breaststroke': 'C', 'butterfly': 'D', 'freestyle': 'B'}

# 最少时间
cost[row_ind, col_ind].sum()
# 163.89999999999998