A/B 测试一般是比较实验组和对照组在某些指标上是否存在差异,当然更多时候是看实验组相比对照组某个指标表现是否更好。
这样的对比在统计学上叫做两样本假设检验,即实验组和对照组为两样本,假设检验的原假设Ho:实验组和对照组无显著差异;备择假设H1:实验组和对照组存在显著差异。
显然,如果实验选取的样本很小,实验结果可信度就不高,因为很可能抽取的样本不能代表真实的水平。而在实际中,因为各种成本的考量,实验样本量也不可能无限大。那么,一般至少需要多少样本才能得到可信的结论呢?
实验所需样本量的一般公式
统计学里有最小样本量计算的公式,公式如下:

样本量计算公式
其中n是每组所需样本量,因为A/B测试一般至少2组,所以实验所需样本量为2n;α和β分别称为第一类错误概率和第二类错误概率,一般分别取0.05和0.2;Z为正态分布的分位数函数;Δ为两组数值的差异,如点击率1%到1.5%,那么Δ就是0.5%;σ为标准差,是数值波动性的衡量,σ越大表示数值波动越厉害。
从这个公式可以知道,在其他条件不变的情况下,如果实验两组数值差异越大或者数值的波动性越小,所需要的样本量就越小。
比例类数值所需样本量的计算
实际A/B测试中,我们关注的较多的一类是比例类的数值,如点击率、转化率、留存率等。
这类比例类数值的特点是,对于某一个用户(样本中的每一个样本点)其结果只有两种,“成功”或“未成功”;对于整体来说,其数值为结果是“成功”的用户数所占比例。如转化率,对于某个用户只有成功转化或未成功转化。
比例类数值的假设检验在统计学中叫做两样本比例假设检验。其最小样本量计算的公式为:
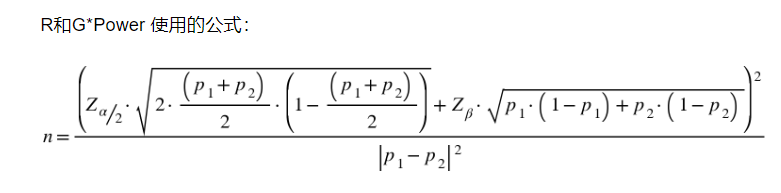
R和G*Power使用的样本量计算公式
上面式子中p1我们称为基础值,是实验关注的关键指标现在的数值(对照组);p2我们称为目标值,是希望通过实验将其改善至的水平;第一类错误和第二类错误上边已经提到,暂不多做说明,通常设定α为0.05,β为0.2 。
既然样本量计算的公式已经清楚,那么我们按照公式代入即可得到结果。这里介绍5种获得比例类数值实验所需样本量的方法,分别为在线工具、Excel、R、Python、G*Power。
以下将以以p1=0.3,p2=0.305,α=0.05,β=0.2为例,演示在这几个工具里计算样本量的方法。
用在线工具计算所需样本量
Evan's Awesome A/B Tools 是一个被使用较多的在线工具,使用起来非常方便,如图:
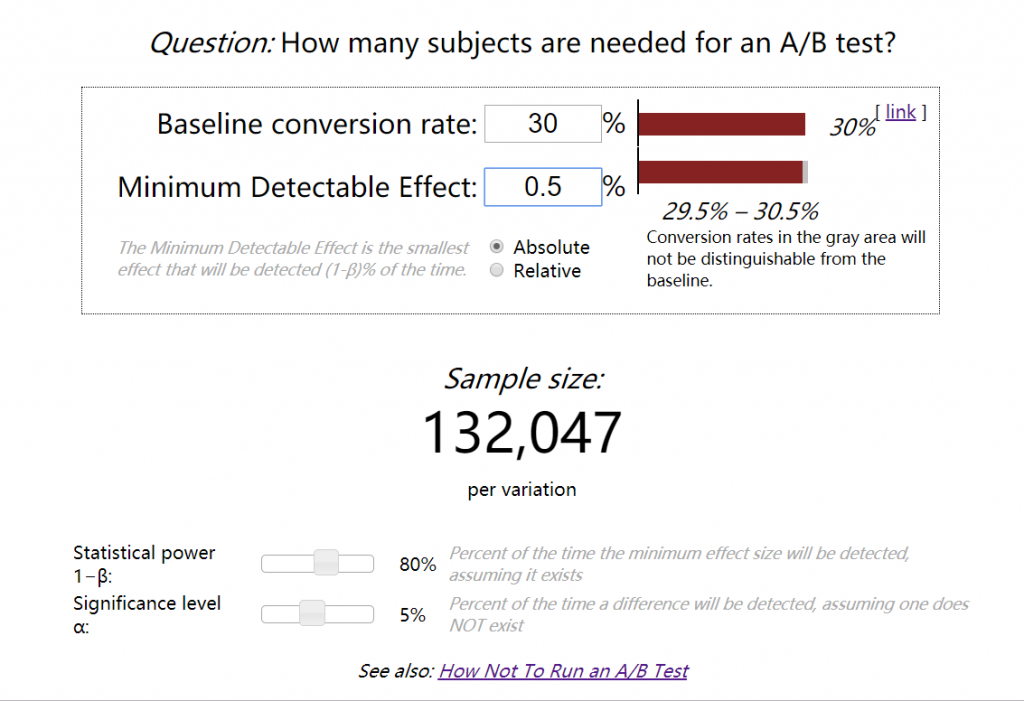
在线计算所需样本量
简单输入几个,底下就显示了结果:每组大约需要132047的样本量。
在Excel中计算所需样本量
在Excel中用上NORM.S.INV等函数,即可实现样本量计算。如图:
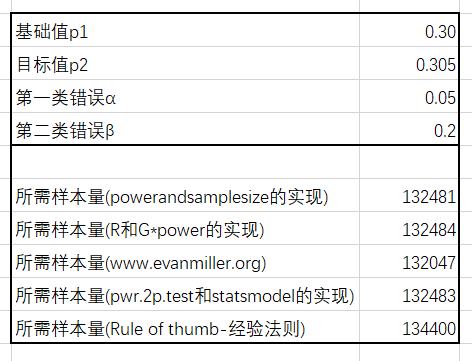
Excel中计算所需样本量
C7-C11的公式分别为:
C7:=(NORM.S.INV(C4/2)+NORM.S.INV(C5))^2*(C2*(1-C2)+C3*(1-C3))/(C3-C2)^2
C8:=(NORM.S.INV(C4/2)*SQRT(2*(C2+C3)/2*(1-(C2+C3)/2))+NORM.S.INV(C5)*SQRT(C2*(1-C2)+C3*(1-C3)))^2/(C3-C2)^2
C9:=(NORM.S.INV(C4/2)*SQRT(2*C2*(1-C2))+NORM.S.INV(C5)*SQRT(C2*(1-C2)+C3*(1-C3)))^2/(C3-C2)^2
C10:=2*(NORM.S.INV(C4/2)+NORM.S.INV(C5))^2/(2*ASIN(SQRT(C2))-2*ASIN(SQRT(C3)))^2
C11:=16*(C2*(1-C2))/(C3-C2)^2
在R中计算所需样本量
R中可以直接使用power.prop.test函数实现。一行代码就可搞定:
| 1 |
|
执行后立即得到输出结果,结果中n即为每组所需的样本量。
R中计算所需样本量
在Python中计算所需样本量
Python中科学计算库里statsmodel也可直接支持计算。具体代码为:
| 1 2 3 4 |
|
执行后得到结果:

Python中计算所需样本量
在G*Power中计算所需样本量
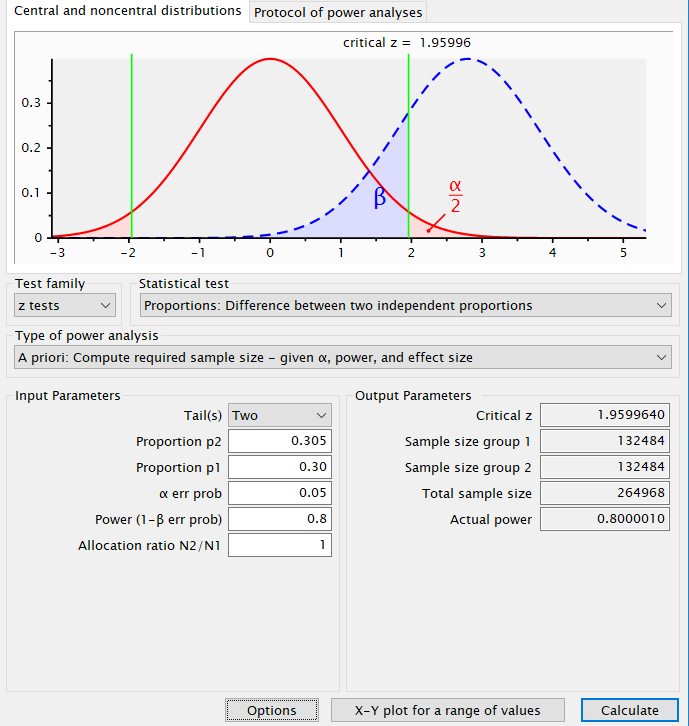
打开G*Power,选取Test family、Statistical test和Type of power analyisis为如下截图所示且输入对应数值。A/B 测试一般是实验组和对照组样本一样多,故N2/N1设为1。
点击Calculate,得到Sample size group1和Sample size group2即为对照组和实验组所需的样本量。