马逸文. 多智能体系统滞后一致性研究[D].西南民族大学,2021.DOI:10.27417/d.cnki.gxnmc.2021.000193.

第一章 绪论

第三章 二阶离散线性多智能体系统滞后一致性

3.5 数值仿真

$$\begin{array}{rl}{x}_0(k+1)& =A{x}_0(k)+v_0(k)\\ v_0(k+1)& =B{v}_0(k)\end{array}$$

$$\begin{array}{rlr}{x}_i(k+1)& =A{x}_i(k)+v_i(k)& \\ v_i(k+1)& =B{v}_i(k)& +a\sum _{j=1}^n{w}_{ij}(x_j(k)-x_i(k))\\ & & -b(x_i(k)-x_0(k-\tau ))\\ & & -c(v_i(k)-v_0(k-\tau ))\end{array}$$

---

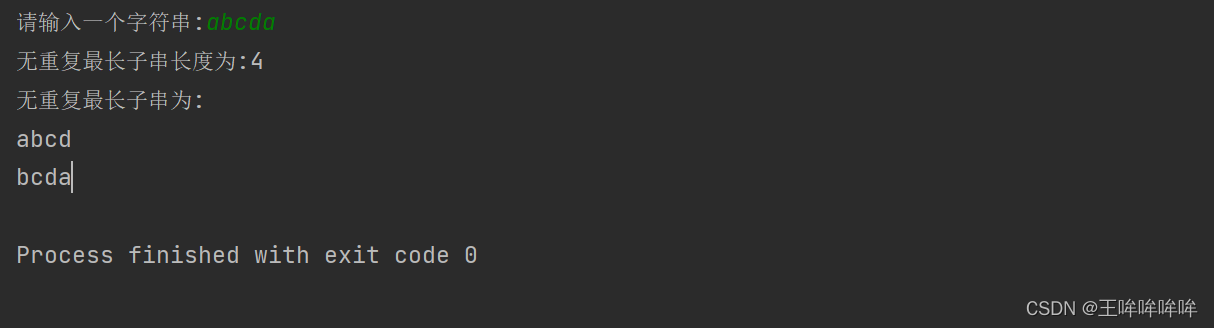
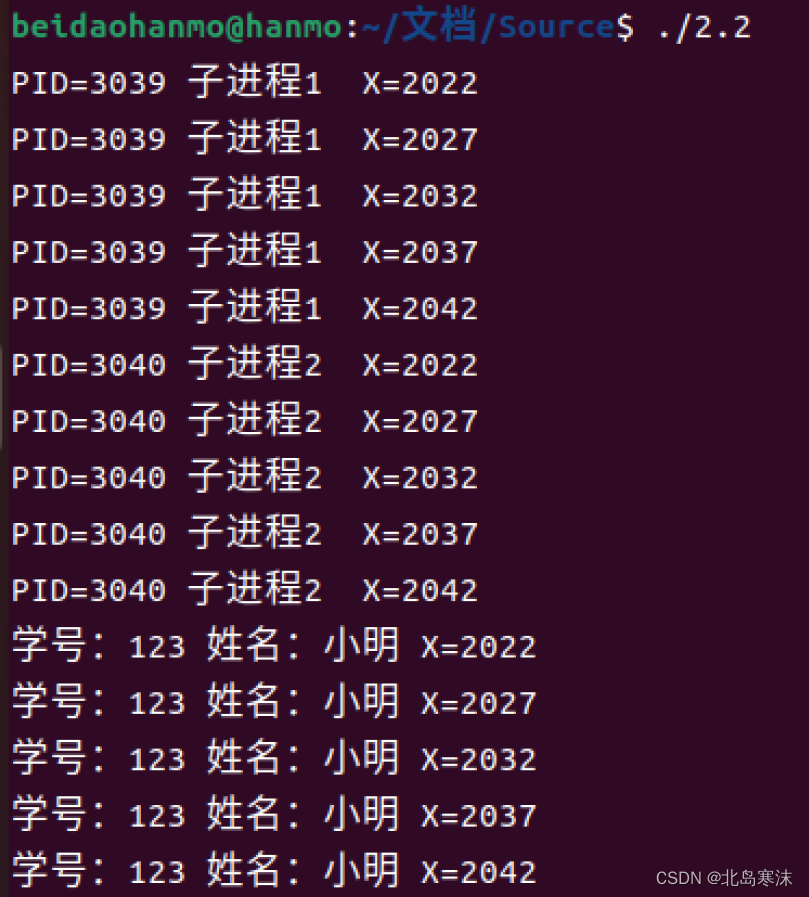
利用基础参数得到的结果如下，对应程序 Main.m

考虑时滞 $\tau =0.15$ 的情况，对应程序 Main_Tau.m

在上述基础上，修改 $A=\left[\begin{array}{cc}-0.5& -0.75\\ 1& -0.5\end{array}\right]$，对应程序 Main_Tau1.m，结果为

在上述基础上，修改 $A=\left[\begin{array}{cc}1& -1.25\\ -1& -1\end{array}\right]$，对应程序 Main_Tau2.m，结果为

在上述基础上，修改 $A=\left[\begin{array}{cc}0.5& -0.25\\ 1& 0.5\end{array}\right]$，对应程序 Main_Tau3.m，结果为

在上述基础上，修改 $A=\left[\begin{array}{cc}0.5& 1.5\\ 1& 0.5\end{array}\right]$，对应程序 Main_Tau4.m，结果为

可以看到结果并不收敛，同时发现特征根并不与论文一致，计算出来的特征根为 ${\lambda }_1=1.7247,{\lambda }_2=-0.7247$。

自己尝试了一下矩阵，将 $A$ 改为 $A=\left[\begin{array}{cc}0.5& 0.15\\ 0.1& 0.5\end{array}\right]$ 后，效果还算理想，效果如下。

---

$$\begin{array}{rl}{x}_0(k+1)& =A{x}_0(k)+v_0(k)\\ v_0(k+1)& =B{v}_0(k)+r_0(k)\\ r_0(k+1)& =C{r}_0(k)\end{array}$$

$$\begin{array}{rlr}{x}_i(k+1)& =A{x}_i(k)+v_i(k)& \\ v_i(k+1)& =B{v}_i(k)+r_i(k)& \\ r_i(k+1)& =C{r}_i(k)& +a\sum _{j=1}^n{w}_{ij}(x_j(k)-x_i(k)+v_j(k)-v_i(k))\\ & & -b(x_i(k)-x_0(k-\tau ))\\ & & -c(v_i(k)-v_0(k-\tau ))\\ & & -d(r_i(k)-r_0(k-\tau ))\end{array}$$