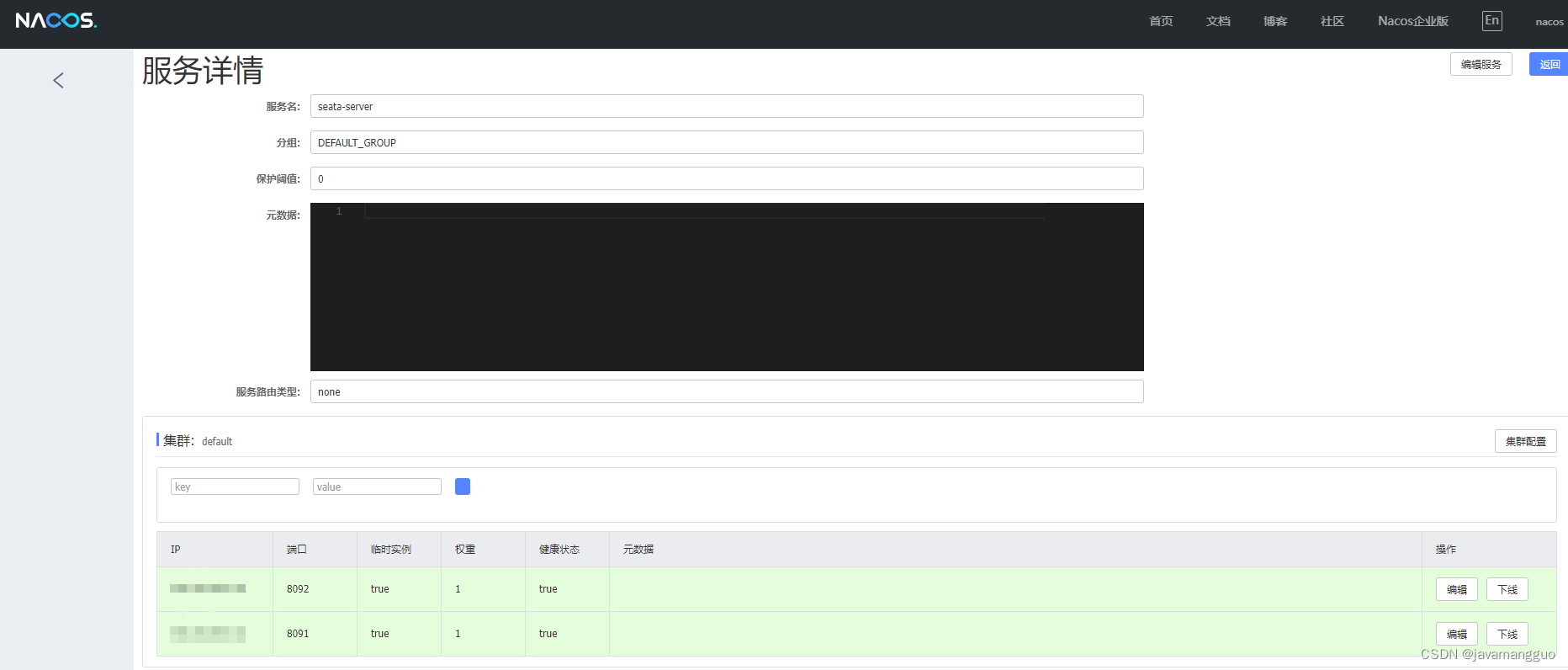
Problem - 1703G - Codeforces

有n个箱子。第i个箱子里有ai个硬币。你需要按顺序打开所有n个箱子，从箱子1到箱子n。

你可以用两种类型的钥匙来打开箱子。

一把好钥匙，使用它需要花费k个硬币。
坏钥匙，不需要花费任何金币，但会将每个未打开的箱子里的所有金币减半，包括它要打开的箱子。减半的操作将使每个被减半的箱子减至最接近的整数。换句话说，用一把坏钥匙打开i号箱子会做ai=⌊ai2⌋，ai+1=⌊ai+12⌋，...，an=⌊an2⌋。
任何钥匙（包括好的和坏的）在使用后都会断掉，也就是说，它是一次性的使用。
你总共需要使用n把钥匙，每个箱子一把。最初，你没有金币，也没有钥匙。如果你想使用一把好钥匙，那么你需要购买它。

在这个过程中，你可以负债；例如，如果你有1个硬币，你可以购买一把价值k=3个硬币的好钥匙，你的余额将变成-2个硬币。

请找出从1号箱子到n号箱子的顺序打开所有n个箱子后，你能拥有的最大数量的硬币。

输入
第一行包含一个整数t（1≤t≤104）--测试案例的数量。

每个测试案例的第一行包含两个整数n和k（1≤n≤105；0≤k≤109）--分别为箱子的数量和一把好钥匙的成本。

每个测试案例的第二行包含n个整数ai（0≤ai≤109）--每个箱子里的硬币数量。

所有测试案例的n之和不超过105。

输出
对于每个测试案例，输出一个单一的整数--按照从箱子1到箱子n的顺序打开箱子后所能获得的最大硬币数。

请注意，有些测试案例的答案不适合32位整数类型，所以你应该在你的编程语言中至少使用64位整数类型（如C++的long long）。

例子
inputCopy
5
4 5
10 10 3 1
1 2
1
3 12
10 10 29
12 51
5 74 89 45 18 69 67 67 11 96 23 59
2 57
85 60
输出拷贝
11
0
13
60
58
备注
在第一个测试案例中，一个可能的策略是如下的。

用5个金币购买一把好钥匙，然后打开1号箱子，得到10个金币。你目前的余额是0+10-5=5个硬币。
用5个硬币买一把好钥匙，然后打开箱子2，得到10个硬币。你目前的余额是5+10-5=10个硬币。
用一把坏钥匙打开3号箱子，由于使用了坏钥匙，3号箱子的硬币数变成⌊32⌋=1，4号箱子的硬币数变成⌊12⌋=0，你现在的余额是10+1=11。
使用一把坏钥匙，打开4号箱子。由于使用了一把坏钥匙，4号箱子里的硬币数量变成了⌊02⌋=0，你现在的余额是11+0=11。
在这个过程结束时，你有11个硬币，这可以证明是最大的。

题解:

根据每次用坏钥匙,当前位及后面所有宝箱金币数均减半(代表后面不会再用好钥匙了,因为除了2,比起以前再用好钥匙会更小)

再结合数据范围1e9,顶多32次后,i + 32后的宝箱就全为0了

那么我们直接暴力枚举再0~n位,每个i后顶多32次就结束了,是可行的

 

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<map>
#include<vector>
#include<queue>
using namespace std;
#define int long long
//1 1 3 3 3
int a[300050];
int s[300050];
int b[300050];
void solve()
{
	int n,k;
	cin >> n >> k;
	for(int i =  1;i <= n;i++)
	cin >> a[i];
	int s = 0;
	int ans = 0;
	for(int i = 0;i < n;i++)
	{
		int ss = s;
		for(int j = i+1;j <= min(n,i+32);j++)
		{
			int cnt = a[j];
			cnt >>=j - i;
			ss += cnt;
		}
		ans = max(ss,ans);
		s += a[i+1] - k;
	}
	ans = max(ans,s);
	cout<<ans<<"\n";
	
	
}
signed main()
{
	int t = 1;
	cin >> t;
	while(t--)
	{
		solve();
	}
}
//2 5
//3
//9 7 


//2  3 4 3