聚类分析
文章目录
- 聚类分析
- 一、聚类分析的概念
- 二、相似性的测度
- 1.距离的四条基本公理
- 2.欧氏距离(Euclid,欧几里得)--距离
- 3.马氏距离(Maharanobis)
- 4.马氏距离与欧氏距离之间的关系
- 5.明氏距离(Minkowaki)
- 6.汉明距离(Hamming)
- 7.角度相似性函数
- 8.应用举例:计算两个文档的距离
- 三、聚类准则
- 1.定义
- 2.确定聚类准则的两种方式
- 3.聚类准则函数
- 四、基于距离阈值的聚类算法
- 1.近邻聚类法
- 2.最大最小距离算法(小中取大距离算法 )
- 五、系统聚类法(层次/分级聚类法)
- 1.算法介绍
- 2.类间距离计算准则
- 参考文献:
一、聚类分析的概念
1.属于非监督分类;
2.难点:
- 特征选择
- 测量值的量化
二、相似性的测度
1.距离的四条基本公理
- d(x,y) >= 0,对于任意的x,y∈P(两点之间的距离大于0)
- d(x,y) = 0, 当且仅当x=y(相同输入,距离为0)
- d(x,y) = d(y,x),对于任意的x,y∈P(对称性)
- d(x,y) <= d(x,z) + d(z,y),对于任意的x,y,z∈P(满足三角不等式)
2.欧氏距离(Euclid,欧几里得)–距离

注意:将特征数据标准化,使其与变量的单位无关。
3.马氏距离(Maharanobis)

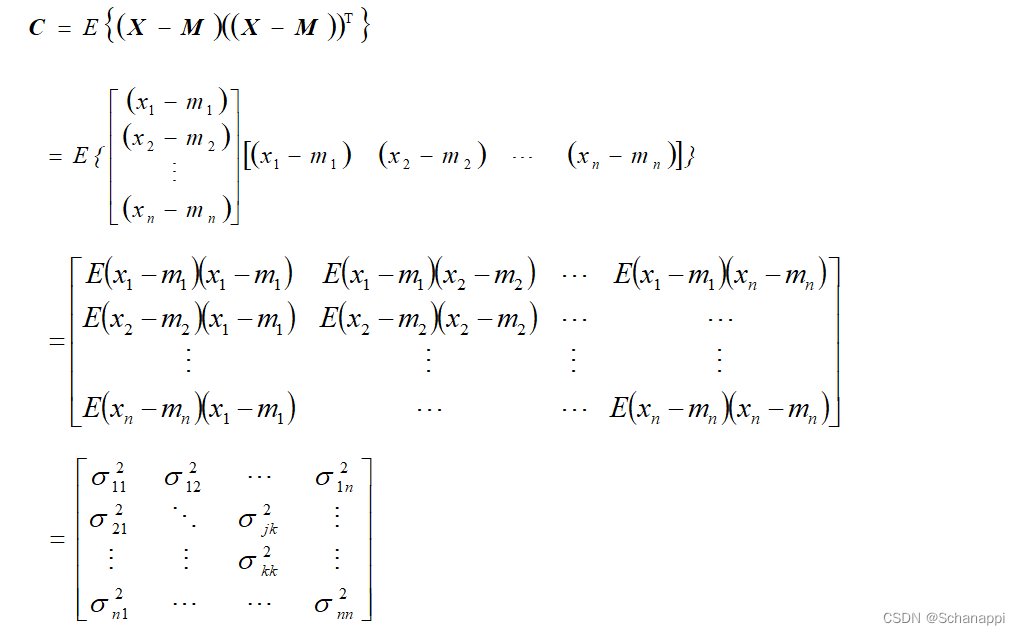

4.马氏距离与欧氏距离之间的关系
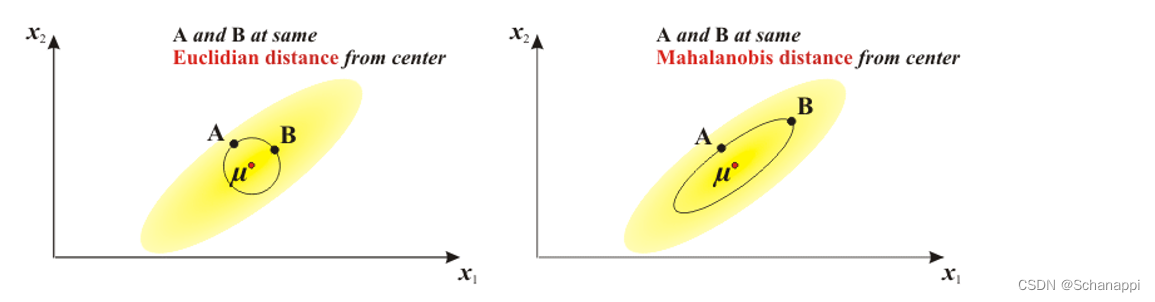
马氏距离的计算是建立在总体样本的基础上的。也就是说,相同的两个样本,如果放入两个不同的总体中,最后计算得出的两个样本之间的马氏距离通常是不相同的。
- 当C=I(单位矩阵)时,马氏距离等于欧氏距离。
5.明氏距离(Minkowaki)
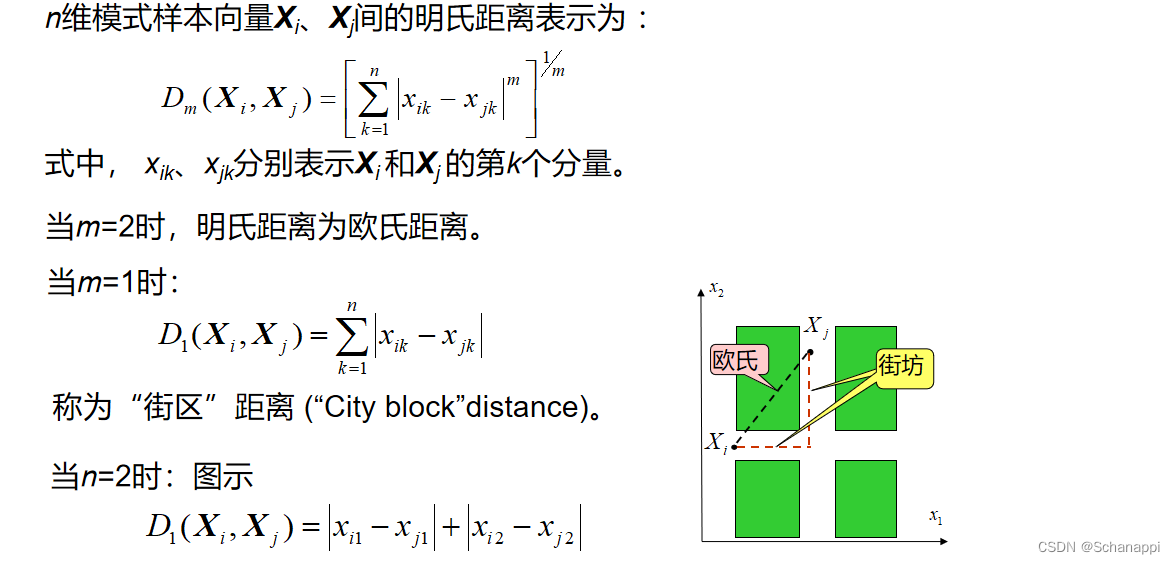
明氏距离适用于多维连续空间中两个点位置的判断。每个空间内的数值必须是连续的。这一类距离定义包括:欧几里得距离(欧氏距离),曼哈顿距离,切比雪夫距离。 而这一族距离的定义,统称为闵可夫斯基距离(明氏距离)。
m取1或2时的明氏距离是最为常用的:
- m=2即为欧氏距离
- m=1时则为曼哈顿距离
- 当m取无穷时的极限情况下,可以得到切比雪夫距离
以2维空间为例,欧氏距离即两点之间的直线距离。曼哈顿距离就是各坐标差的绝对值的和。而切比雪夫距离则是各坐标上差的绝对值的最大值。
明氏距离(曼哈顿距离、欧氏距离和切比雪夫距离)的缺点:
- 各个分量的单位必须是等价的。如果有量纲不相等的维度,就无法适用。
举例来说,考虑楼宇内的定位问题:水平方向上的单位是米,垂直方向的单位是”层“,在这种情况下就无法直接使用明氏距离。
解决办法:需要对数据做正规化;- 没有考虑各个分量的分布(期望,方差等)可能是不同的 ;
- 各个维度必须是互相独立的,也就是“正交”的。
马氏距离针对上述第1,3个缺点做出了改进。
它是一种有效的计算两个未知样本集的相似度的方法。
与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的),并且是尺度无关的(scale-invariant),即独立于测量尺度。
6.汉明距离(Hamming)

举例:
d(10010,10000) = 1
d(abcbc,abdab) = 3
7.角度相似性函数
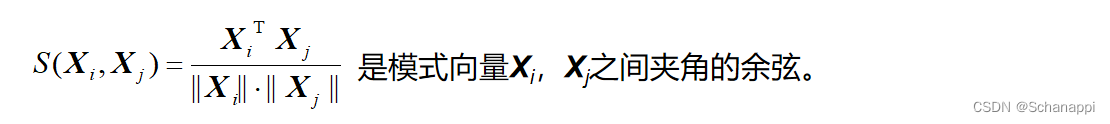
8.应用举例:计算两个文档的距离
- 文本特征向量化
- 统计各词在文档中是否出现(词集模型)
OneHot编码向量化文本:只要单个文本中单词出现在字典中,就将其置为1,不管出现多少次。- 统计各词在文档中出现次数(词袋模型)
TF(词频)、TF-IDF(词频-逆文档频率)
- 计算向量之间的距离

三、聚类准则
1.定义
根据相似度测度确定的,衡量模式之间是否相似的标准。把不同模式聚为一类还是归为不同类的准则。
2.确定聚类准则的两种方式
- 阈值准则:根据规定的距离阈值进行分类
- 函数准则:利用聚类准则函数进行分类
3.聚类准则函数

四、基于距离阈值的聚类算法
1.近邻聚类法


2.最大最小距离算法(小中取大距离算法 )

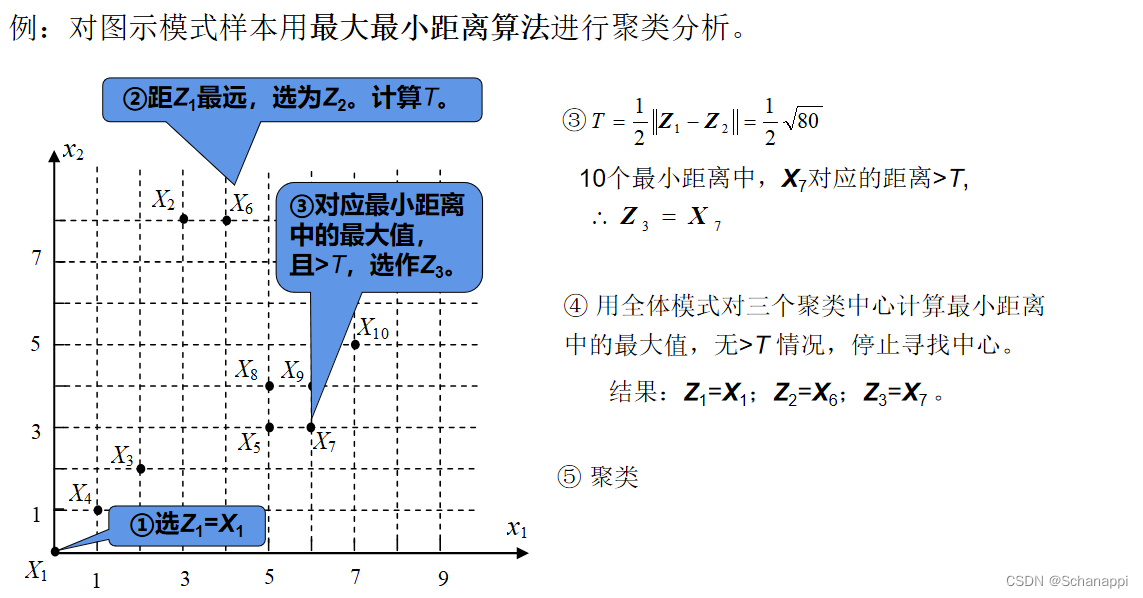
五、系统聚类法(层次/分级聚类法)
1.算法介绍

2.类间距离计算准则
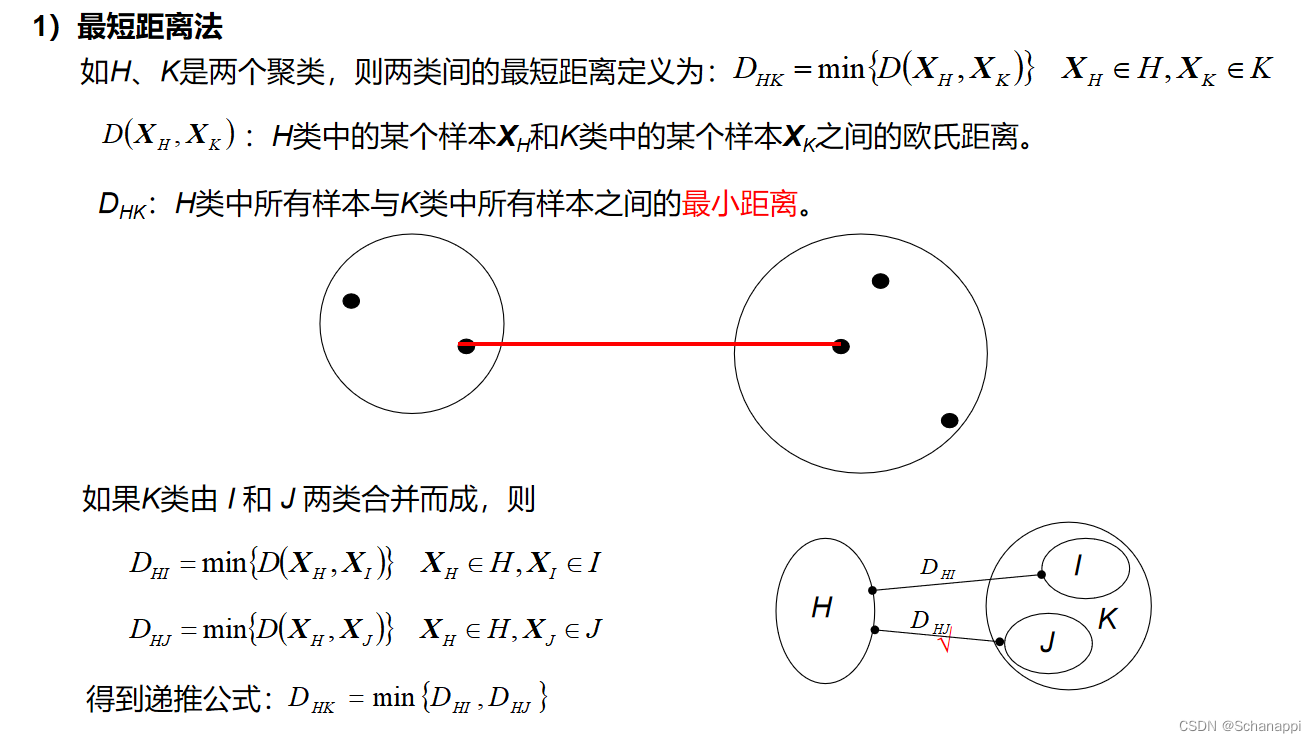
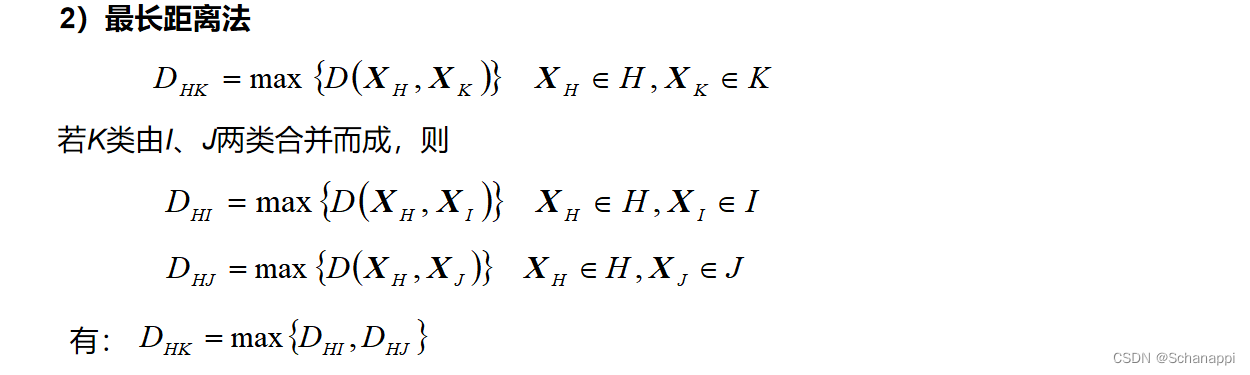
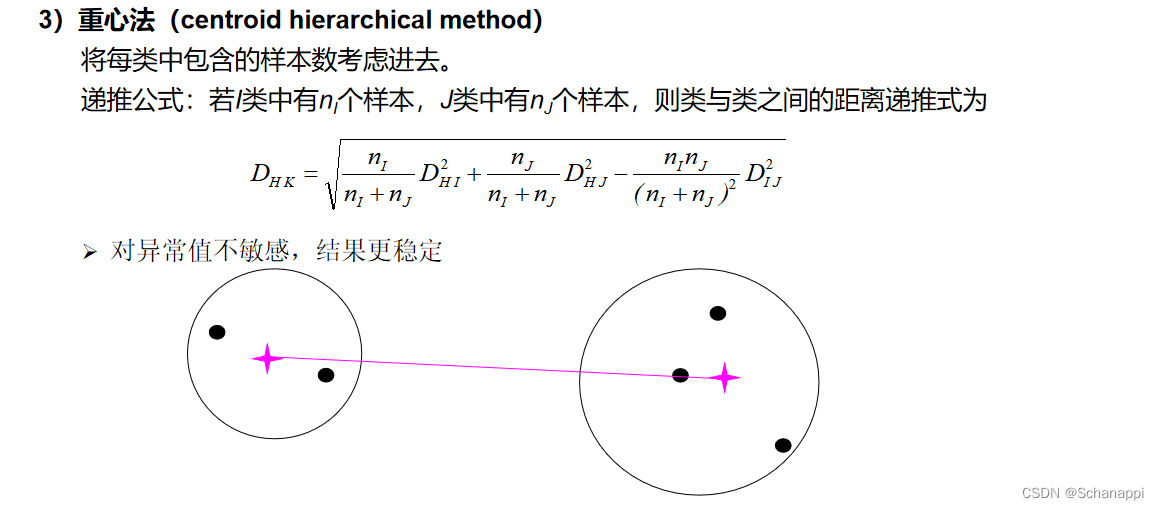

以上距离准则算法需要掌握,有例题。
参考文献:
[1]各种距离的归纳和总结