本文重点解决如下几个问题：

（1）什么是蒙特卡洛法？

（2）蒙特卡洛法能够解决什么问题？

（3）蒙特卡洛法的优势是什么？或者说为什么要使用蒙特卡洛法？

 

一、理论基础

1.1 伯努利大数定理

    进行N次独立重复实验，随着试验次数的增大，事件A发生的频率$\frac{n_A}{N}$依概率收敛为事件A发生的概率$p_A$；

1.2 辛钦大数定理

    一个独立同分布(iid)的随机变量序列$x_1,x_2,x_3,...,x_n$，具有数学期望$\mu$，从随机序列中抽样一部分样本记作集合$X_s$，则有$E(X_s)=\mu$，即随着样本量$n$的增大，样本均值收敛为总体均值。

1.3 切比雪夫大数定理

    设随机变量序列$x_1,x_2,x_3,...,x_n$两两互不相关，且期望存在$E(X_i)={\mu }_i$，方差存在且有共同有界上限，即： $$D(X_i)={\sigma }_i^2<M$$则随着样本容量的增加，样本平均数收敛于总体平均数。

1.4 三者区别和联系

• 伯努利大数定理揭示了频率和概率的关系；
• 辛钦大数定理揭示了算术平均值和数学期望的关系；
• 切比雪夫大数定理揭示了样本均值和真实期望的关系（相较于辛钦大数定理，切比雪夫大数定理并未要求同分布，更具有一般性）。

    总结来看，大数定理将属于数理统计的平均值和属于概率论的期望联系在了一起。

二、蒙特卡洛法

2.1 蒙特卡洛的起源

    蒙特卡洛是摩纳哥的著名赌城，该法为表明其随机抽样的本质而命名。

    蒙特卡洛法（Monte Carlo Method）也称统计模拟法、统计实验法，是把概率现象作为研究对象的数值模拟方法，是按抽样调查法求取统计值推定未知特性量的计算方法。该方法通过构造一个和系统相似的概率模型，在数字计算机上进行随机试验来模拟系统的随机特性，故适用于对离散系统进行仿真实验，特别适用于一些解析法难以求解甚至无法求解的问题。

    蒙特卡洛并不是什么高深的理论，只是一种 基于大数定理的方法或策略。 它是用抽样后的样本发生的频率来估计概率，所以它求得的是近似解，而不是精确解，随着样本数的增多，近似解越接近精确解。蒙特卡洛方法本身不是优化算法，与遗传算法、粒子群算法等优化算法有着本质区别。

    蒙特卡洛法的理论基础是概率统计理论；

    蒙特卡洛法的主要手段/实现方法是随即抽样、统计实验。

2.2 蒙特卡洛的解题思路

   蒙特卡洛的基本步骤：

• 第一步，建立一个概率模型或随机过程，它的参数或数字特征近似于问题的解；

• 第二步，给出模型中各种不同分布随机变量的抽样方法；

• 第三步，通过对模型或过程的观察或抽样实验，来计算这些参数或数字特征。

    总之，蒙特卡洛方法有三个主要步骤：构造概率模型；利用概率分布抽样；建立各种估计量。

    对于可以用解析法求解的简单的问题，蒙特卡洛是一个“笨办法”，但对于许多难以求解的问题，蒙特卡洛方法是有效甚至是唯一可行的办法。

2.2 蒙特卡洛法的应用

• 计算定积分；
• 超越积分的数值计算（牛顿-莱布尼茨公式难以求解），比如$y=sin(x^2)$，$y=e^{a{x}^2}$等；
• 求不规则图形的面积；
• 求$\pi$；
• 风险评估；
• ……

三、几个小栗子

3.1 求解定积分

$$y={\int }_0^{10}{x}^{2}dx$$

3.1.1 解析法

$$y={\int }_0^{10}{x}^{2}dx=\frac{1}{3}{x}^3{|}_0^{10}=\frac{1}{3}\times 10^3-\frac{1}{3}\times 0^3=\frac{1000}{3}$$

3.1.2 蒙特卡洛法

    蒙特卡洛法求定积分有两种方法：随机投点法、期望法（或称平均值法），本文重点讲解随机投点法。随机投点法求解定积分的思路是：该题$x\in [0,10],y\in [0,100]$，因此在$10\times 100$的矩形区间内均匀撒点，统计落在曲线下方的点的个数占比，再乘以矩形区间面积就是定积分的值。注意：这个例子的曲线完全位于$x$坐标轴上方，所以不需要考虑正负号，如果面积有正有负，需要先划分区域，分区计算再求和！

    定积分的本质是求和横坐标围成的有符号面积，因此蒙特卡洛方法有一个弊端：只能求在定积分区间函数值为恒非负或恒非正的函数的定积分，如果积分区间有正有负，那么只能将区间拆分成多个子区间分别进行计算再相加！

%% 蒙特卡洛方法近似求解定积分
% 积分曲线：y = x ^ 2
% 定积分区间：[0, 10]

%% Matlab代码 
clear; clc; close all; warning off;
rng(0);
set(0,'defaultAxesFontName', 'Monospaced');  % 防止中文乱码

% 离散化
L = 10;  % 积分长度
fs = 1 / 1e3;  % 采样率
x = 0 : fs : L;  
y = x .^ 2;  
S = L * (L ^ 2);  % 样本空间面积

% 在区间内撒样本
N_Lis = [1e1, 1e2, 1e3, 1e4];  % 样本个数列表

% 求解定积分
res_integ = 1/3 * (10^3 - 0^3); % 解析解
figure(1); clf;
for n = 1 : length(N_Lis)
    cnt = 0;
    x_random = L * rand(1, N_Lis(n));  % 随机点x
    y_random = L ^ 2 * rand(1, N_Lis(n));  % 随机点y
    for i = 1 : N_Lis(n)
        if y_random(i) <= x_random(i) ^ 2
            cnt = cnt + 1;
        end
    end    
    res_appro = cnt / N_Lis(n) * S;  % 近似解
    
    % 作图
    subplot(2, 2, n);
    plot(x, y, 'k', 'linewidth', 2); hold on;
    area(x, y, 'facecolor', [0, 1, 1]); hold on;
    scatter(x_random, y_random, 10, 'r', 'filled', 'markerfacealpha', 0.5);
    xlabel('x'); ylabel('y'); set(gca, 'fontsize', 14);
    title(['解析解≈', num2str(res_integ, '%.1f'), '   近似解≈', num2str(res_appro, '%.1f')]);
end
f = suptitle('求解y=x^2定积分');
set(f, 'fontsize', 18); set(gcf, 'position', [12, 60, 1450, 650]);

运行结果：

    从上面运行结果可以发现，随着样本点数的增加，近似解越来越接近真实的解析解。

3.2 求解六边形面积

    图形是由六条直线围成的六边形，六条直线分别为：
$$\{\begin{array}{ll}& y1=1\\ & y2=-x+2\\ & y3=x+2\\ & y4=3\\ & y5=-x+5\\ & y6=x-1\end{array}$$

3.2.1 解析法

    这个图形是由上下两个梯形构成的，因此它的面积为：
$$S=(1+3)\times 1÷2\times 2=4$$

3.2.2 蒙特卡洛法

    使用蒙特卡洛法求解不规则面积的思路是：不规则图案一定位于某个规则矩形内，矩形的面积很容易求得，点位于不规则形状内的概率为$p=\frac{A_{shape}}{A}$。因此，重复往矩形范围内撒点，那么当样本点数足够大时，撒入不规则图案内的点数占比（频率）约等于点落入不规则形状内的概率。即：
$$p=\frac{A_{shape}}{A}\approx \frac{n}{N}$$
    不规则图形区间$\Omega$可用如下数学式表示：
$$\Omega =y\ge 1且y\ge -x+2且y\le x+2且y\le 3且y\le -x+5且y\ge x-1$$
即蒙特卡洛法的“击中”区间。因此有，蒙特卡洛法的Matlab代码如下：

%% 蒙特卡洛方法近似求解图形面积
clear; clc; close all; warning off;

% 产生图形
L = 4;  % 区间矩形边长
fs = 1 / 1e3;
x1 = 1 : fs : 2;
y1 = 1 * ones(1, length(x1));
x2 = 0 : fs : 1;
y2 = -x2 + 2;
x3 = 0 : fs : 1;
y3 = x3 + 2;
x4 = 1 : fs : 2;
y4 = 3 * ones(1, length(x4));
x5 = 2 : fs : 3;
y5 = -x5 + 5;
x6 = 2 : fs : 3;
y6 = x6 - 1;

S = L * L;

% 计算图形面积
res_integ = (1 + 3) * 1 /2 * 2;
N_Lis = [1e1, 1e2, 1e3, 1e4];
figure(1); clf;
for n = 1 : length(N_Lis)
    cnt = 0;
    x_random = L * rand(1, N_Lis(n));
    y_random = L * rand(1, N_Lis(n));
    for i = 1 : N_Lis(n)
        if (y_random(i)>=1) && (y_random(i)>=-x_random(i)+2) && (y_random(i)<=x_random(i)+2) ...
                && (y_random(i)<=3) && (y_random(i)<=-x_random(i)+5) && (y_random(i)>=x_random(i)-1)
            cnt = cnt + 1;
        end
    end
    res_appro = cnt / N_Lis(n) * S;
    
    % 作图
    subplot(2, 2, n);
    plot(x1, y1, 'k', 'linewidth', 2); hold on;
    plot(x2, y2, 'm', 'linewidth', 2); hold on;
    plot(x3, y3, 'g', 'linewidth', 2); hold on;
    plot(x4, y4, 'y', 'linewidth', 2); hold on;
    plot(x5, y5, 'b', 'linewidth', 2); hold on;
    plot(x6, y6, 'r', 'linewidth', 2); hold on;
    h = fill([1, 2, 3, 2, 1, 0], [1, 1, 2, 3, 3, 2], 'c');
    scatter(x_random, y_random, 10, 'r', 'filled', 'markerfacealpha', 0.5); hold off;    
    xlabel('x'); ylabel('y'); title(['样本数=', num2str(N_Lis(n)), '   解析解=', num2str(res_integ), '   近似解≈', num2str(res_appro, '%.2f')]); 
    set(gca, 'fontsize', 14); set(h, 'edgealpha', 0, 'facealpha', 0.3);
end
h = suptitle('蒙特卡洛法求图形面积');
set(h, 'fontsize', 18);
set(gcf, 'position', [12, 60, 1450, 650]);

运行结果：

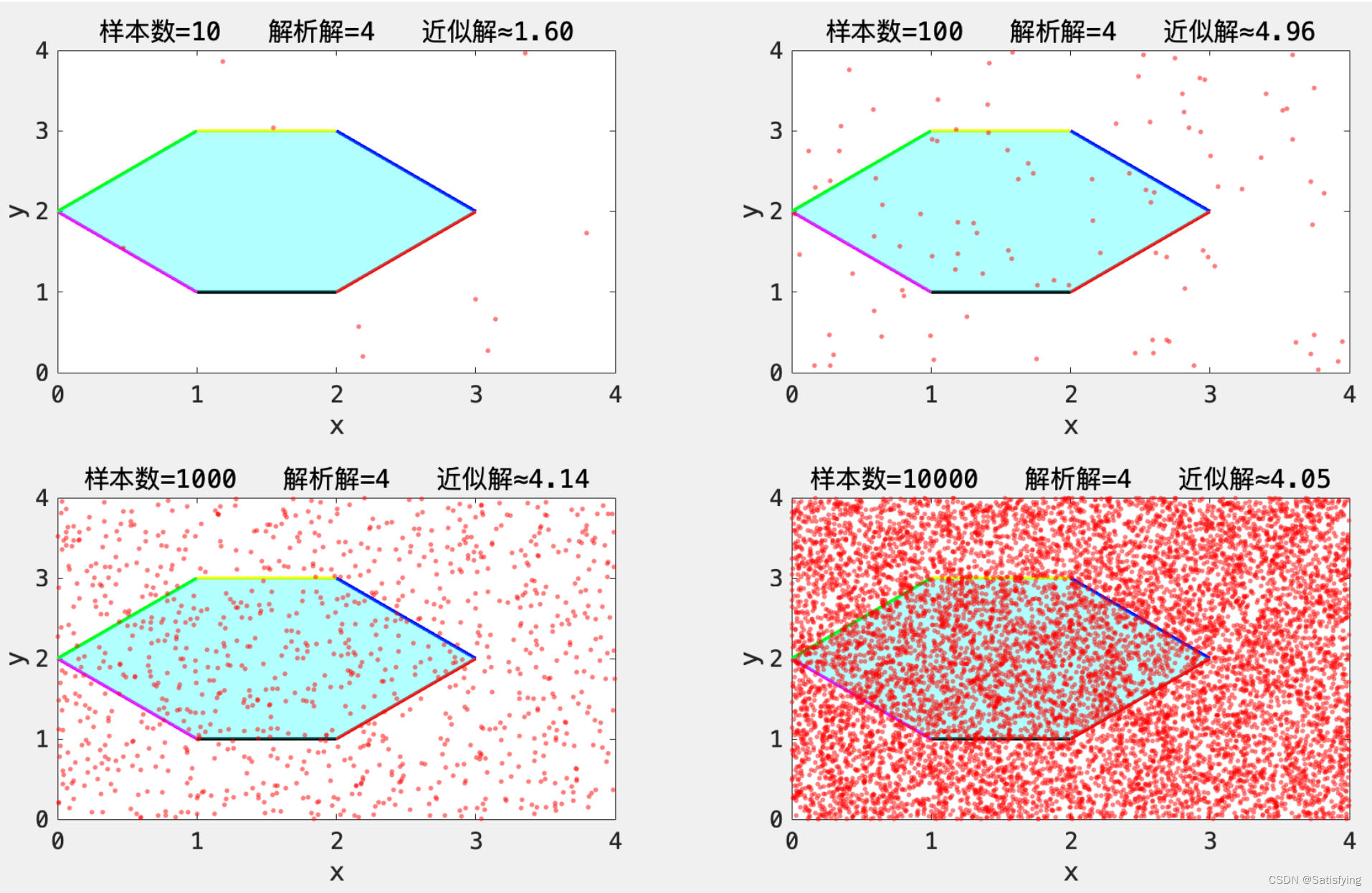
    有人会有疑问了，上面两个例子都可以通过规则的定积分公式、规则图形面积计算公式求得，那为什么还需要用蒙特卡洛法呢？蒙特卡洛法看起来并没有解析解求解过程简单，那么蒙特卡洛法存在的意义是什么？

    一个问题解决这个疑问：如果遇见没有面积计算公式的不规则图形，它的面积该怎么计算？有人要说了，用定积分啊！那么我再问，如果围成这个不规则图形的曲线函数不可积呢？那解析解就无法计算了，这时候只能用蒙特卡洛法求解近似解了。

3.3 求解不规则图形面积

    图形是由三条曲线围成的不规则图形，三条曲线分别为：
$$\{\begin{array}{ll}& y1=sin(x^2)\\ & y2=\frac{sin(x)}{x}\\ & y3=e^{-x^2}\end{array},0\le x\le 2$$
    如下，下面两张图分别是三个函数的曲线和其围成的面积。

    对围成区域$\Omega$的面积进行如下建模：
{ S = ∫ ∫ Ω 1 d x d y Ω = { ( x ,   y ) ,    0 ≤ x ≤ 2   且   y ≤ s i n ( x 2 )   且   y ≤ s i n ( x ) x   且   y ≥ e − x 2 } \begin{cases}&S=\int\int_{\Omega}1dxdy\\&\Omega=\{(x,\,y),\,\, 0\leq x\leq2\,且\,y\leq sin(x^2)\,且\,y\leq \frac{sin(x)}{x}\,且\,y\geq e^{-x^2}\}\\\end{cases} {​S=∫∫Ω​1dxdyΩ={(x,y),0≤x≤2且y≤sin(x2)且y≤xsin(x)​且y≥e−x2}​
即：
$$\{\begin{array}{ll}S& ={\int }_0^2{\int }_{e^{-x^2}}^{min(sin(x^2),\frac{sin(x)}{x})}1dydx\\ & ={\int }_0^{2}y{|}_{e^{-x^2}}^{min(sin(x^2),\frac{sin(x)}{x})}dx\\ & ={\int }_0^{2}min(sin(x^2),\frac{sin(x)}{x})-e^{-x^2}dx\end{array}$$
    如果数学功底比较好的朋友，可以一眼看出来这三个函数都是不可积函数。此例无法用解析法求解，下面重点介绍蒙特卡洛法的应用。

    蒙特卡洛法的思路是：在$2\times 3$的矩形区间内均匀撒点，统计落在区域内的点的个数占比，再乘以矩形区间面积就是围成图形的面积近似值，样本点个数越大，近似值越接近真实值。

    围成区域空间$\Omega$，即蒙特卡洛法的“击中”区间。因此有，蒙特卡洛法的Matlab代码如下：

%% 蒙特卡洛求解解析解无法求解的问题
clear; clc; close all; warning off;

% 生成三个不可积的信号
T = 20;
fs = 1 / 1e3;
x0 = -T : fs : T;
y1 = sin(x0.^ 2);
y2 = sin(x0) ./ x0;
y3 = exp(-x0.^2);

figure(1); clf;
subplot(3, 1, 1);
plot(x0, y1, 'linewidth', 1.5); ylabel('y'); title('y=sin(x^2)'); set(gca, 'fontsize', 12);
subplot(3, 1, 2);
plot(x0, y2, 'linewidth', 1.5); ylabel('y'); title('y=sin(x)/x'); set(gca, 'fontsize', 12);
subplot(3, 1, 3);
plot(x0, y3, 'linewidth', 1.5); xlabel('x'); ylabel('y'); title('y=e^{-x^2}'); set(gca, 'fontsize', 12);

% 绘制围成区域
x = 0 : fs : 2;
y11 = sin(x.^ 2);
y21 = sin(x) ./ x;
y31 = exp(-x.^2);

figure(2); clf;
plot(x, y11, 'linewidth', 1.5); hold on;
plot(x, y21, 'linewidth', 1.5); hold on;
plot(x, y31, 'linewidth', 1.5); hold on;
area(x(y11>y31 & y21>y11), y11(y11>y31 & y21>y11), 'facecolor', 'c', 'edgealpha', 0); hold on;
area(x(y11>y31 & y21>y11), y31(y11>y31 & y21>y11), 'facecolor', 'w', 'edgealpha', 0); hold on;
h = legend('y=sin(x^2)', 'y=sin(x)/x', 'y=e^{-x^2}', 'location', 'southwest');
xlabel('x'); ylabel('y'); title('求三条曲线围成的面积'); set(gca, 'fontsize', 12); set(h, 'fontsize', 12);

% 蒙特卡洛法求面积
L = 2; 
H = 3;
S = L * H;
N_Lis = [1e1, 1e2, 1e3, 1e4];
figure(3); clf;
for n = 1 : length(N_Lis)
    N = N_Lis(n);
    x_random = L * rand(1, N);
    y_random = H * rand(1, N) - 1;
    cnt = 0;
    for i = 1 : N
        if (y_random(i) <= sin(x_random(i)^2)) && (y_random(i) <= sin(x_random(i))/x_random(i)) ...
                && (y_random(i) >= exp(-x_random(i)^2))
            cnt = cnt + 1;
        end
    end
    res_appro = cnt / N * S;
    
    subplot(2, 2, n);
    plot(x, y11, 'linewidth', 1.5); hold on;
    plot(x, y21, 'linewidth', 1.5); hold on;
    plot(x, y31, 'linewidth', 1.5); hold on;
    area(x(y11>y31 & y21>y11), y11(y11>y31 & y21>y11), 'facecolor', 'c', 'edgealpha', 0); hold on;
    area(x(y11>y31 & y21>y11), y31(y11>y31 & y21>y11), 'facecolor', 'w', 'edgealpha', 0); hold on;
    scatter(x_random, y_random, 10, 'r', 'filled', 'markerfacealpha', 0.5);
    xlabel('x'); ylabel('y'); title(['样本数=', num2str(N_Lis(n)), '   近似解≈', num2str(res_appro, '%.2f')]); 
    set(gca, 'fontsize', 14); 
end

h = suptitle('蒙特卡洛法求图形面积');
set(h, 'fontsize', 18);
set(gcf, 'position', [12, 60, 1450, 650]);

运行结果：

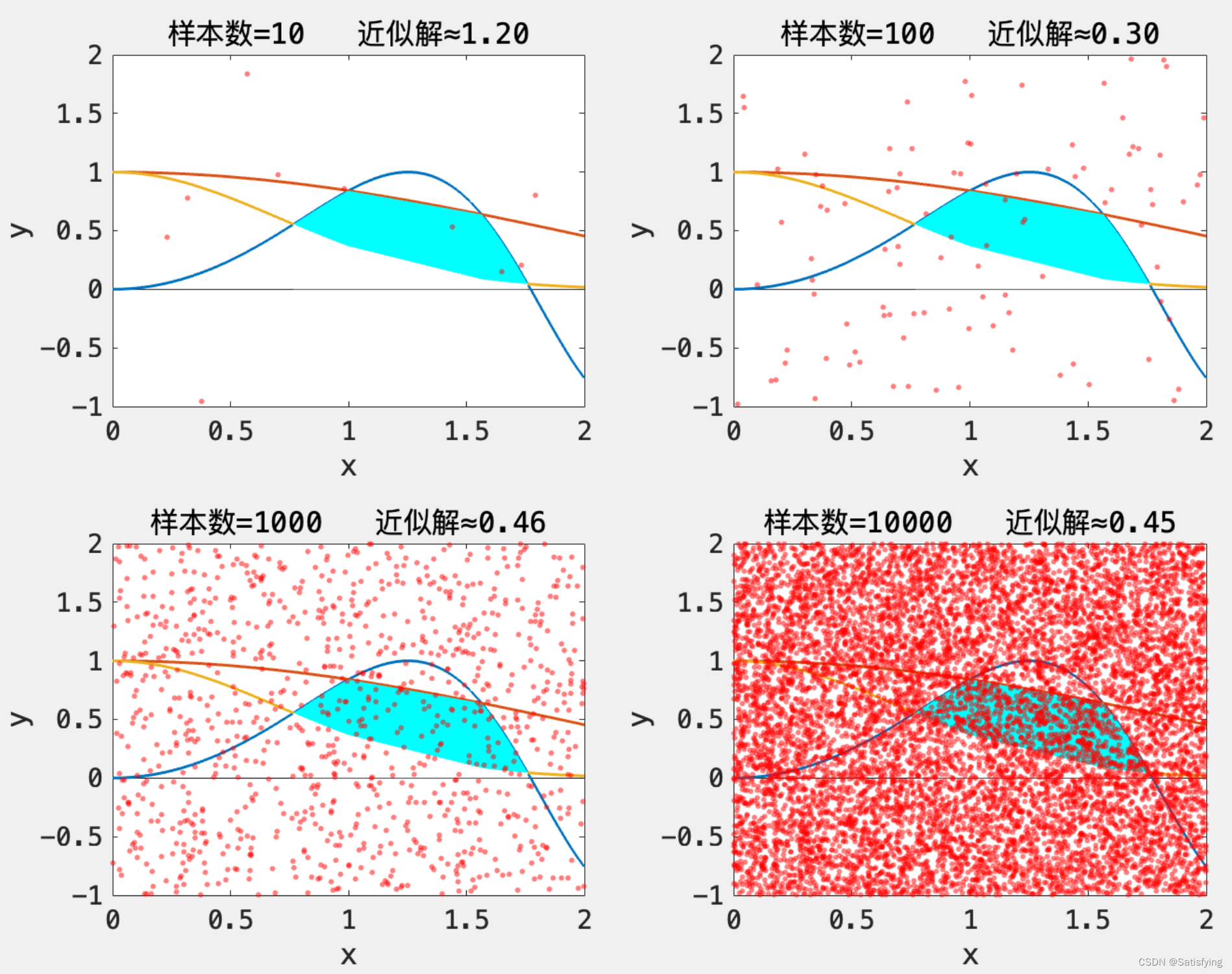
四、总结

    蒙特卡洛法不是一种优化算法，是基于大数定理的一种离散化的解题策略，尤其适用于问题的解析解难以计算或者甚至没有解析解时。

    

    （本文完整的pdf请关注“张张学算法”，并回复“011”获取~）