资源限制
内存限制：256.0MB C/C++时间限制：1.0s Java时间限制：3.0s Python时间限制：5.0s
问题描述
　　那个曾经风靡全球的贪吃蛇游戏又回来啦！这次贪吃蛇在m行n列的网格上沿格线爬行，从左下角坐标为(0,0)的格点出发，在每个格点处只能向上或者向右爬行，爬到右上角坐标为(m-1,n-1)的格点时结束游戏。网格上指定的格点处有贪吃蛇喜欢吃的豆豆，给定网格信息，请你计算贪吃蛇最多可以吃多少个豆豆。
输入格式
　　输入数据的第一行为两个整数m、n（用空格隔开），分别代表网格的行数和列数；第二行为一个整数k，代表网格上豆豆的个数；第三行至第k+2行是k个豆豆的横纵坐标x、y（用空格隔开）。
输出格式
　　程序输出一行，为贪吃蛇可吃豆豆的最大数量。
样例输入
10 10
10
3 0
1 5
4 0
2 5
3 4
6 5
8 6
2 6
6 7
3 1
样例输出
5
数据规模和约定
　　1 ≤ m, n ≤ 10⁶，0 ≤ x ≤ m-1，0 ≤ y ≤ n-1，1 ≤ k ≤ 1000
题目链接：网格贪吃蛇

分析：

  看完题，相信小伙伴很容易就会想到状态转移方程：因为$dp[i][j]$一定是$dp[i-1][j]$或者$dp[i][j-1]$转移过来的，但是一看数据规模，若开10⁶ 的二维 int 型数组(4 X 10⁶ X 10⁶ / 1024 / 1024 = 3814697MB)，内存超限。
  再看 k 最大不超过 1000，将这 1000 个点离散化即可，开 10³ 的二维数组是不会内存超限的。
（PS：这是我第一次做离散化的题，看了相关知识点的视频，结合例子去理解到的，离散化的概念我就不赘述了，小伙伴可以先去搜索离散化的概念，再结合我的题解进行理解）。

思路：

  将所有点的横、纵坐标都存进同一个数组，然后从小到大排序，各个数字对应一个数组下标，将原来的点映射在新的以数组下标构成的坐标系，这就将其离散化了。下面结合例子以及图片进行理解。
假设有三个点（5，10），（41，16），（100，37），若以常规的100X100的坐标系，那么会有很多的空间浪费，

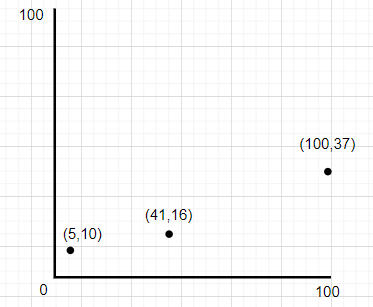
将其横纵坐标离散化，映射在新的坐标系：

那么原来的各个点在新坐标系的位置为：
  (5,10) -> (0,1)， (41,16) -> (4,2)， (100,37) -> (5,3)
这样就将 100X100 的空间减小到了 5X5，极大的节省了空间，这是解决本题的核心。

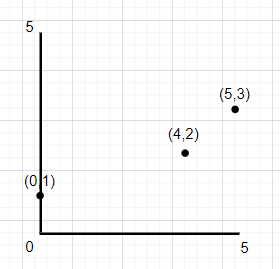
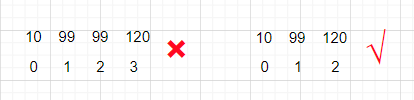
注意：在进行离散化时，需要对数字进行去重，避免出现以下的情况，不然映射新的坐标系会产生歧义，导致错误：

代码（细节写在了注释）：

import java.util.Arrays;
import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;

public class Main {
	static int m, n, k;
	static dot[] dots = new dot[1005];	//存放点的数组
	//长度为2000是因为横纵坐标都要映射为数组下标，共2000
	static int[][] g = new int[2010][2010];	//新的坐标系
	static int[][] dp = new int[2010][2010];
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		m = sc.nextInt(); n = sc.nextInt(); k = sc.nextInt();
		//存横纵坐标的数字的集合，采用HashSet自动去重
		Set<Integer> nums = new HashSet<>();
		for (int i = 1; i <= k; i++) {
			int x = sc.nextInt();
			int y = sc.nextInt();
			dots[i] = new dot(x, y);	//将点放入点数组
			nums.add(x);	//将x，y加入集合
			nums.add(y);
		}
		Integer[] arrNums = nums.toArray(new Integer[nums.size()]);	//set转为数组
		Arrays.sort(arrNums);	// 排序/离散化，每个数字对应一个数组下标
		for (int i = 1; i <= k; i++) {	//将原来各坐标映射到新坐标系
			int x = find(dots[i].x, arrNums);//找到映射的点(x,y)
			int y = find(dots[i].y, arrNums);
			//这里的x，y都是从0开始，我习惯从1开始，就加了1，也方便后面dp的运算
			g[x+1][y+1] = 1;	
		}
		int len = arrNums.length;
		for (int i = 1; i <= len; i++) {
			for (int j = 1; j <= len; j++) {
				dp[i][j] = g[i][j];
				dp[i][j] += Math.max(dp[i-1][j],dp[i][j-1]);
			}
		}
		System.out.println(dp[len][len]);
	}
	public static int find(int x, Integer[] arr) {//二分查找映射的下标
		int l = 0, r = arr.length - 1;
		while(l < r) {
			int mid = (l + r) >> 1;
			if(x == arr[mid])
				return mid;
			if(x < arr[mid])
				r = mid;
			else l = mid + 1;
		}
		return l;
	}
}
class dot{
	int x, y;
	public dot(int x, int y) {
		this.x = x;
		this.y = y;
	}
}