目录
4.1.树
4.2.二叉树
4.2.1.概述
4.2.3.存储结构
4.2.3.遍历
1.逻辑简介
2.代码示例
4.1.树
树,由n(n≥0)个有限节点和边组成一个具有层次关系的数据结构。树需要满足以下条件:
- 任何结点的子节点不相交。
- 任何子结点只有一个父节点。
- N个结点,N-1条边。
对于一个非空树(结点数≥0),具有以下性质:
- 起始结点称为“根”
- 除根结点外可分为m个互不相交的有限集合,其中每个集合本身也是一棵树,称为原来这棵树的“子树”。
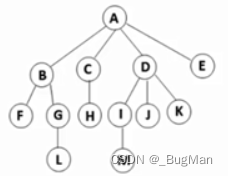
树的基本术语:
- 结点的度:节点的子树个数
- 树的度:树的所有结点中最大的度数
- 叶结点:度为0的结点
- 父结点:有子树的结点都是它的子树的根结点
- 子结点:若A是B的父结点,则B是A的子节点
- 兄弟结点:具有同一父结点的结点彼此是
4.2.二叉树
4.2.1.概述
二叉树是一种每个结点的度不大于2的树,由根结点和左子树、右子树组成,具有以下五种姿态:
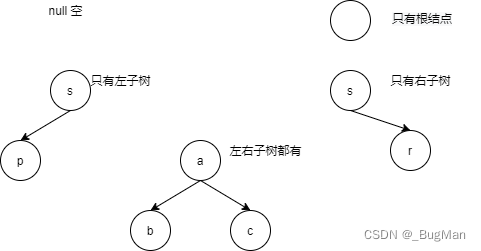
除了五种基本姿态外,还有三种比较特殊的姿态:
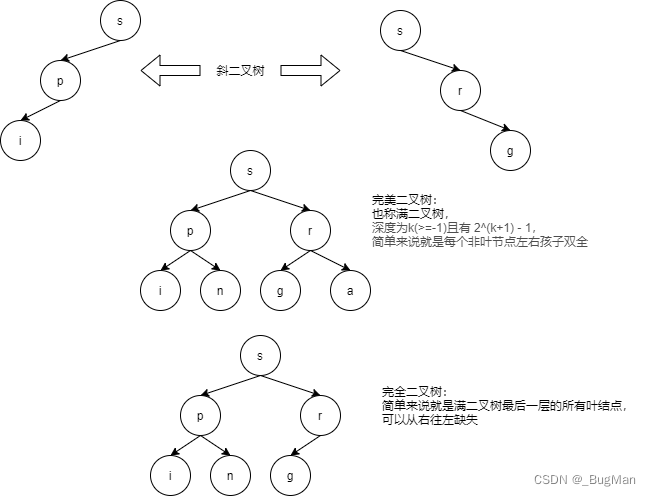
4.2.3.存储结构
二叉树可以用两种结构存储,一种是链表,一种是数组。
数组表示的话第一个位置存储的根结点,挨着根结点的是根结点的左右孩子,接下来是根结点左孩子的左右孩子,右孩子的左右孩子,以此类推:

数组仅适合完全二叉树(完美二叉树是特殊的完全二叉树),以为当表示非完全而二叉树,会出现大面积内存空间浪费的情况:
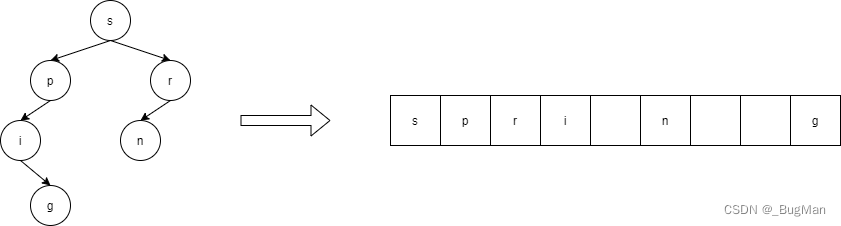
4.2.3.遍历
1.逻辑简介
二叉的遍历,本质上是二维结构的线性化,二叉树本来是非线性的,但是其结果最后是线性的。
二叉树的遍历根据访问当前子树的根结点的顺序分为四种:
- 先序遍历
- 中序遍历
- 后序遍历
除此之外还有一种特殊的遍历,层序遍历,按照每一层来遍历。

层序遍历需要用到一个队列来实现:
首先是根结点入队,然后访问根结点,根结点左右孩子顺序入队,根结点出队,然后队列中的后续结点重复上述的出队入队流程,直到队列为空,整个层序遍历过程就结束。

2.代码示例
二树的结点:
public class Node {
//数据域
private int data;
//指针域
private Node left;
private Node right;
//遍历标志
private boolean isOrder;
{
isOrder=false;
}
public Node(){
}
public Node(int data){
this.data=data;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
public boolean isOrder() {
return isOrder;
}
public void setOrder(boolean order) {
isOrder = order;
}
}各种遍历的实现:
public class BinaryTree {
//判断BT是否为空
public static boolean isEmpty(Node root){
//判断操作
return root==null?true:false;
}
//先序建树
public static Node create(Node node,Scanner scanner){
Integer data=Integer.parseInt(scanner.next());
if(data!=-1){
node=new Node();
node.setData(data);
node.setLeft(create(node,scanner));
node.setRight(create(node,scanner));
}
//以防万一,如果节点为叶节点时,将其左右指针置空
if(data==-1){
node.setLeft(null);
node.setRight(null);
}
return node;
}
//递归先序遍历二叉树
public static void pre(Node node){
//需要给节点增加一个遍历状态标志位
//每次递归回溯时需要判断当前节点的标志位是否为已遍历状态
//否则会徘徊在叶节点,堆栈溢出
if(node!=null&!node.isOrder()){
System.out.println(node.getData());
node.setOrder(true);
pre(node.getLeft());
pre(node.getRight());
}
}
//中序遍历
public static void mid(Node node){
if(node!=null&!node.isOrder()){
node.setOrder(true);
mid(node.getLeft());
System.out.println(node.getData());
mid(node.getRight());
}
}
//后续遍历
public static void post(Node node){
if(node!=null&!node.isOrder()){
node.setOrder(true);
mid(node.getLeft());
mid(node.getRight());
System.out.println(node.getData());
}
}
//层序遍历
public static void level(){
//递归法
if (!queue.isEmpty()) {
//取出队首元素
Node node = queue.exit();
//打印节点数据
System.out.println(node.getData());
//左孩子入队
queue.Enter(node.getLeft());
//右孩子入队
queue.Enter(node.getRight());
level();
}
//循环法
/*while (!queue.isEmpty()) {
//取出队首元素
Node node = queue.exit();
//打印节点数据
System.out.println(node.getData());
//左孩子入队
queue.Enter(node.getLeft());
//右孩子入队
queue.Enter(node.getRight());
}*/
}
}需要注意的是,层序遍历的话要用到一个队列来实现,这个队列的话用的就是之前在线性结构里实现的那个队列:
public class queue {
private static Node[] que;
//头指针
private static int first;
//尾指针
private static int last;
//初始化
static{
que=new Node[100];
first=0;
last=-1;
}
//入队
public static void Enter(Node node){
que[++last]=node;
}
//出队
public static Node exit(){
Node node=que[first++];
return node;
}
//判空
public static boolean isEmpty(){
return (que[first]==null&&first==last) ? true:false;
}
}