1. 版本设计
实验版本的设计要遵循变量的单一性,不能一下子改变多个因素,如同一个按钮不能同时改变按钮颜色和按钮文字,实验设计越简单越容易得出正确的结论。
案例时间:
2. 实验时长
业界的实验时长一般是2-3周,最短时长建议不要少于7天。因为不同日期活跃的用户群体可能不一样,所以最好要覆盖一个周期,如7天、14天、21天。
那实验时长是不是越长越好呢,也不是的,实验时间过长会把各版本的区别拉平了,不同时期用户对不同策略的反应不一样。
例如0元夺宝玩法刚出来的时候用户会特别感兴趣,时间久了大家都知道这是一个套路会慢慢免疫选择性忽略掉,在玩法诞生之初进行实验可能效果会很显著,时间长了之后这玩法的效果就会慢慢下降。
实验结果也是有时效性的,仅对当前时间当前用户群有效果并不是放之四海而皆准,所以实验时间不宜过长,应快速验证快速迭代。
3. 选择指标
一个改动影响的指标可能是多方面的,例如更改了加购物车按钮的颜色,点击该按钮的人可能会增多,从而间接导致下单的人数增多。那如何从众多指标当中选择出实验效果指标呢?
既然直接效果指标已经可以决定实验的成败,为什么还要添加其他间接指标呢,这就涉及到一个取舍问题了,不是实验成功了就一定要上线最佳版本。
假如实验版本确实有提升,但付出的成本有点大,那就要权衡下利弊再决定要不要上线新版本。又或者实验版本对我们想要提升的指标有显著效果,但影响到了其他指标的大幅下降,这时候也需要我们进行权衡。
具体可视当前产品北极星指标而定,如当前产品战略目标为营收,该实验虽对用户活跃有影响但能提高营收,也是可以全量上线新版本的,但当前战略目标为有效日活,那就要慎重考虑新版本的上线问题了。
4. 案例时间
基于前面的例子,影响最为直接的指标为点击付费弹窗支付按钮人数,但是这个跟各实验组具体人数也有关系,所以应该转化为比率。
分母应该是点击表情按钮人数而不是展示付费引导弹窗人数,因为两个版本的展示付费引导弹窗触发条件不一样,方案B已经人为的过滤掉一批低质量用户,必然会对展示点击率产生影响。
本实验间接影响的正向指标为付费人数,同理也需转化为付费率。正如产品同学A所说,发表情改为付费发送会降低那些点击表情按钮意欲发表情的用户的体验,有关用户活跃性的指标同时也需要关注,如:人均使用时长、留存率,这些活跃性指标均可作为本实验的负向指标来关注。
5. 计算最小样本量
之所以要计算最小样本量,主要有以下几点原因:
- 样本量太小不能代表整体的情况,容易受到偶然因素影响,这就要求计算出至少抽取多少样本量才能代表整体情况;
- 避免浪费流量,通常有多个迭代同时进行,给其他迭代留出实验空间;
- 如果实验是负向的,可以避免带来大面积不必要的损失。
1)计算最小样本量两种检验方法
Z检验:检验实验组和对照组服从分布的均值是否相等
卡方检验:检验实验组是否服从理论分布(将对照组的分布视为理论分布)
在A/B Test中常见的检验方法为Z检验,下面就以Z检验为例计算最小样本量,在这之前先来了解下以下知识点:
- α:表示出现第一类错误的概率,也称为显著性水平,常见的取值有1%、5%、10%、20%,一般取值5%,即犯第一类错误的概率不超过5%,常见的表示方法为:1-α,称为统计显著性,表示有多大的把握不误诊。
- β:表示出现第二类错误的概率,一般取值20%,更常见的表示方式为统计功效power=1-β,即有多大把握能检查出版本差异。
从两类错误上限的取值(α是5%,β是20%)我们可以了解到A/B Test的重要理念:宁肯砍掉多个好的产品,也不要让一个不好的产品上线。
指标基线:原有方案的指标,有可能是数值,有可能是比率,取决于选择的直接效果指标。这个指标由历史数据得出,如果是一个全新的版本实验没有历史数据,可参考其他类似功能的指标数据,若都没有只能根据经验大概给出一个基准值。
MDE:检验灵敏度,以下用Δ表示,新方案的直接效果指标与指标基线差值的绝对值,即新方案与旧方案的区别有多大,该参数越大需要的样本量越少。
方差:方差的计算方式根据直接核心指标是数值或者比率决定。
单/双尾检验:用哪一种类型检验视原假设而定,若原假设为新旧方案无区别用双尾检验,使用场景为样本量计算或者AA测试;若原假设为新方案优于旧方案或旧方案优于新方案则用单尾检验,后面用到的实验结果评估用的则是单尾检验。
Z值:该值可以依据α和β指标确定出对应的Z值,有固定的Z值表可以查,也可以通过excel的NORMSINV函数计算。
鉴于篇幅问题,后续有时间再专门写一篇详细介绍Z检验,下面直接贴Z检验样本量计算公式出来吧(这里使用双尾检验因此使用α/2):
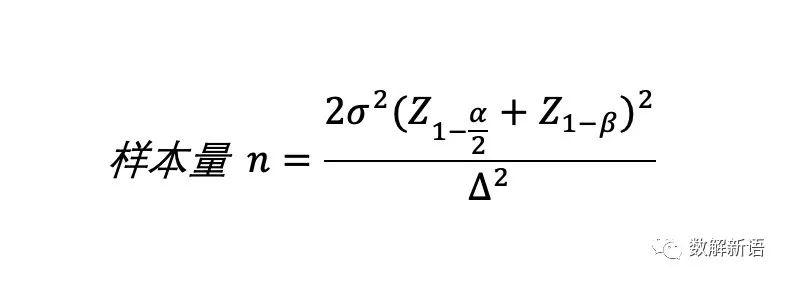
2)案例时间
计算样本量之前首先要获取历史的支付按钮点击率,一般取最近一个月的历史数据,根据历史数据计算出支付按钮点击率均值p:
p=(0.075+0.079+0.087+……+0.083+0.077+0.081) / 30=0.08
- 根据支付按钮点击率均值p计算出方差:
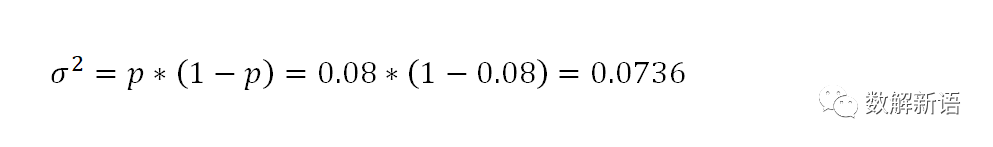
- 确定MDE值,新方案至少比旧方案提升多少才能达到我们的预期,即计算新方案的ROI,避免实际收益不能弥补新方案的研发和推广成本,这里我们取比原方案提升10%,即新方案期望的点击率为:p(新方案支付按钮点击率)=0.08*(1+10%)=0.088,可得MDEΔ=0.088-0.008=0.008;
- 计算Z值,本实验中我们取α=5%,β=20%,通过NORMSINV计算,得:
- 从以上数据,计算最终所需样本量为:
通过以上计算,每个实验组需要18053人,有两个实验组则总需18053*2=36106人。
6. 圈选用户
计算出了实验所需人数,下一步就是从总用户群体中抽取出对应人数进行实验,这一步我们将会面临着两个问题:如何从一个总体中按一定比例抽取随机样本;如果同时进行的实验中有互斥的怎么办。
针对以上两个问题我们有以下三种解决方案,下面分别介绍下:
1)单层方案
所有流量按某个参数(UserID,DeviceID、CookieID、手机号等)分成n个桶,假设选定UserID,有以下两种方法:
以上解决了随机性问题,并没有解决实验互斥的问题,只能靠人工给各实验指定分组进行实验。
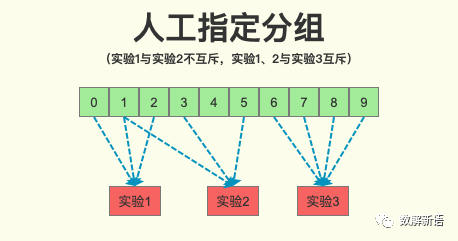
2)多层方案
单层方案适合简单的验证,不适合长期大规模做交叉实验,流量利用效率太低,且随机组不好把握,最终容易造成某一组用户指标明显优于其他组。
为了解决以上问题,多层分组方案应运而生,人为定义一些分层,如:UI 层、推荐算法层,每一层中再对用户随机分组,即可实现同一个用户出现在不同层的不同组里面,做到流量的重复利用。具体实现方法如下:
从上图看到流量经过每一层时都会被打散重新分配,下一层每一组的流量都随机来源于上一层各组的流量,如推荐算法层的0组用户均匀来源于UI层的0、1、2……n组用户。
如此一来我们只需要指定实验处于哪一层,系统就可计算出该层还有多少剩余流量然后自动分配,即使实验不互斥也没必要共用相同的实验组。
3)无层方案
多层方案做到了流量的重复利用,但是并没有发挥出最大的重复利用价值。
单独看每一层,其实就是一个单层方案,并没有从根本上解决问题,只不过是复制出来多几层而已,如果某一层实验非常多,还是会存在流量不够用的情况,这就衍生出了无层方案。
所谓无层,就是每个实验都是单独一层,具体实现方法如下:
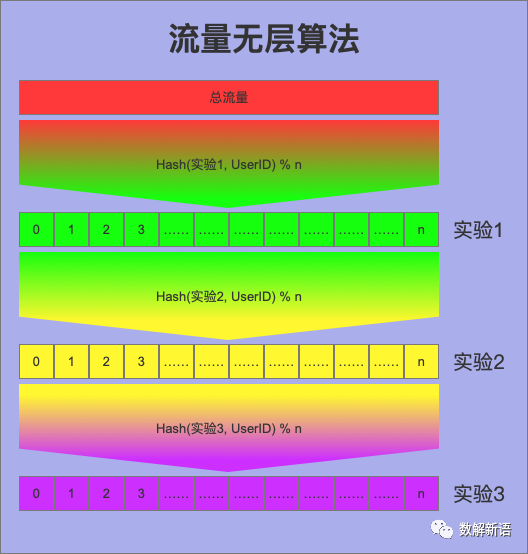
如此一来确保了每个实验都单独占有所有流量,可以取任意组的流量进行实验,但是又引进了新的问题,多层方案将实验的互斥在层内进行了限制,无层会导致同一个用户命中多个实验,即使这些实验是互斥的。
显然这样子是绝对不允许的,解决方法是赋予每个实验优先级,例如按上线优先级排序,优先将流量赋予高优先级用户。也可以在创建实验的时候如果有互斥实验,新创建实验的分组算法复用已有实验的实验ID进行分组即可避免。
以上分流算法最终会形成n个组,需要进行AA实验验证分组是否均匀。验证各组之间无显著性差异后即可从n组中随机抽取出某几组达到实验所需的用户量进行实验。