题目描述

在一个有向无环图中，可能存在多种有效拓扑序列。以下图为例：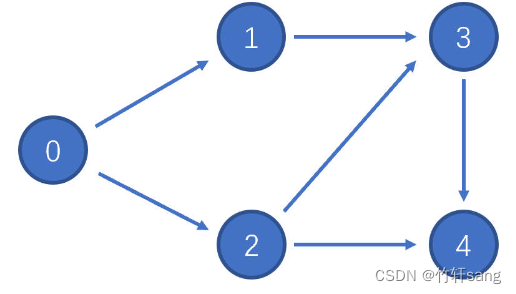

存在两种可行的拓扑序列：
0 1 2 3 4
0 2 1 3 4
本题会给出一个图，以及多个序列，你来判断每一个序列是否是该图的有效拓扑序列。 

输入格式

第一行为2个正整数m和n，分别表示有向无环图的节点个数和边的数量。
接下来n行，代表n条边。分别是起点、终点、权重，以空格分隔。
（m<50,n<100）
接下来为一个正整数o，表示接下来会出现的序列个数。
（o<1000）
再往后是o个序列，序列中的每个值用空格隔开。

输出格式

按行输出：o个序列中，每一个序列是否为图的有效拓扑序列。
是的话输出：YES
不是的话输出：NO

输入样例

5 6
0 1
0 2
1 3
2 3
2 4
3 4
3
0 1 2 3 4
0 2 1 3 4
0 1 3 2 4

输出样例  

YES
YES
NO

代码展示 

思路：循环判断当前结点入度，为零则将其邻接点入度-1，继续判断给定序列的下一结点。若为有效拓扑序列，（入度）则应按序陆续减为0；否则无效。

#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

#define INFO_MAX_SIZE 20
#define MAX_SIZE 200
 //领接矩阵存储的图
struct Graph{
	int vexNumber;
	string vexInfo[INFO_MAX_SIZE];
	int adjMatrix[MAX_SIZE][MAX_SIZE];
};
 //弧结点定义
struct ArcNode{
	int weight;//弧上的信息部分
	int adj;//邻接点的序号
	ArcNode *nextarc;
};
 //顶点结点定义
struct VexNode{
	string Info;
	ArcNode *firstarc;
};
 //领接表结构的图的定义
struct linkGraph{
	VexNode *vexes;
	int vexnumber;
};

struct tempNode{
	int col;
	int row;
	//tempNode *next;
};

struct temp{
	int num;
	tempNode *docu;
};


int preInitGraph(linkGraph &G,const Graph &g){
	G.vexes=new VexNode[g.vexNumber];
	G.vexnumber=g.vexNumber;
	for(int i=0;i<g.vexNumber;i++){
		G.vexes[i].firstarc=NULL;
	}
	return 0;
}
//将邻接矩阵存储的图转换为领接表存储的图
void InitGraph(linkGraph &G,const Graph &g,temp &t){
	preInitGraph(G,g);
	for(int i=0;i<t.num;i++){
		int a,b;
		a=t.docu[i].row;b=t.docu[i].col;
		ArcNode *p=new ArcNode();
		p->nextarc=NULL;
		p->adj=b;
		ArcNode *q=G.vexes[a].firstarc;
		if(G.vexes[a].firstarc==NULL)
			G.vexes[a].firstarc=p;
		else{
			while(q->nextarc!=NULL){
				q=q->nextarc;
			}
			q->nextarc=p;
		}
	}
}

//输出领接表存储的图
void PrintGraph(const linkGraph &G){
	for(int i=0;i<G.vexnumber;i++){
		cout<<G.vexes[i].Info;
		ArcNode *p=G.vexes[i].firstarc;
		cout<<i;
		while(p!=NULL){
			cout<<" --> "<<p->adj;
			p=p->nextarc;
		}
		cout<<endl;
	}
}

int check(linkGraph LG,int a[],int indegree[]){
	//PrintGraph(LG);
	int temp[LG.vexnumber]={0};
	for(int i=0;i<LG.vexnumber;i++)  temp[i]=indegree[i];
	for(int i=0;i<LG.vexnumber;i++){
		if(temp[a[i]]!=0)  return 1;
		for(ArcNode *p=LG.vexes[a[i]].firstarc;p!=nullptr;p=p->nextarc){
			temp[p->adj]--;
		}
	}
	return 0;
}


int main(){
	//freopen("/config/workspace/test/test","r",stdin);
	int n,m;
	cin>>n>>m;

	Graph G;
	G.vexNumber=n;
	temp t;
	t.num=m;
	t.docu=new tempNode[m];
	for(int i=0;i<m;i++){
		int a,b;
		cin>>a>>b;
		t.docu[i].row=a;
		t.docu[i].col=b;
	}
	linkGraph LG;
	InitGraph(LG,G,t);
	int indegree[LG.vexnumber]={0};
	//for(int i=0;i<LG.vexnumber;i++) indegree[i]=0;
	for(int i=0;i<LG.vexnumber;i++){
		for(ArcNode *p=LG.vexes[i].firstarc;p!=nullptr;p=p->nextarc)
			indegree[p->adj]++;
	}//入度
	int k;
	cin>>k;
	for(int i=0;i<k;i++){
		int a[n];
		for(int j=0;j<n;j++){
			cin>>a[j];
		}
		int flag=check(LG,a,indegree);
		if(flag)  cout<<"NO"<<endl;
		else  cout<<"YES"<<endl;
	}
	
	
	return 0;
}

//闲叙题外话：这周事情好多啊。