目录
一、斐波那契数?
二、递归实现求第n个斐波那契数
2.1代码与运行结果
2.1.1图解递归过程
三、非递归求法
3.1为什么不用递归求法
3.2非递归
一、斐波那契数?
它指的是这样的数列:1,1,2,3,5,8,13,21,34,55.......
第一个和第二个数为二,第三个位开始它的值为前两位之和。
二、递归实现求第n个斐波那契数
知道什么是斐波那契数
我们可以得出:
n>2:
Fib(n)=Fib(n-1)+Fib(n-2)
n<=2
Fib(1)=Fib(2)=1
2.1代码与运行结果
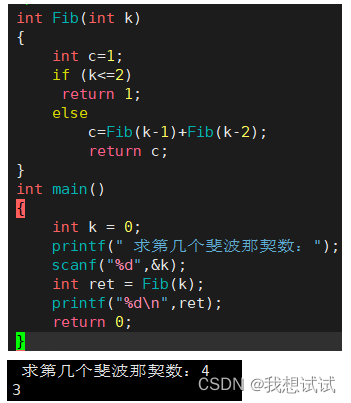
2.1.1图解递归过程
求第4位斐波那契数(红色是调用函数,蓝色是返回函数)
递归需要满足两个条件:
1.有可以结束递归的条件(图中(k<=2)就是)
2.每次递归都会接近这个条件

三、非递归求法
3.1为什么不用递归求法
但是递归似乎并不适用于求斐波那契数。
我们可以看到,它一直再求一些相同的数的值。

这个是求第35个斐波那契数时,所求的第3个斐波那契数的次数。

并且在求一些,值比较大的情况,并不会马上输出结果。
程序没有崩,计算机在拼命的计算。
![]()
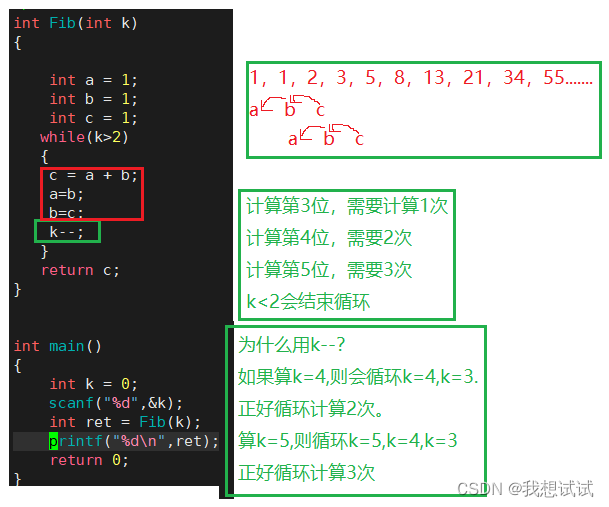
3.2非递归
运算速度会比递归快
![]()
Nothing in the world is difficult for one who sets his mind to it. - MAO zedong.
世上无难事,只怕有心人。——毛泽东