一、相机标定的四个坐标系

1、世界坐标系（Xw，Yw，Zw)：也称真实或现实世界坐标系，或全局坐标系。它是客观世界的绝对坐标，由用户任意定义的三维空间坐标系。一般的3Ｄ场景都用这个坐标系来表示。

世界坐标系的作用：标定时确定标定物的位置；作为双目视觉参考系，给出两个相机相对世界坐标系的关系，从而求出两个相机之间的关系；作为重建得到三维坐标的容器，盛放重建后的物体的三维坐标。

2、摄像机坐标系（Zc,Xc,Yc）：摄像坐标系的原点在摄像机的光心上，z轴与摄像机光轴平行，x，y 一般与图像物理坐标系的Ｘ，Ｙ平行。

摄像机坐标系的作用：世界坐标系的物体需要先进行刚体变化转变到摄像机坐标系（旋转平移），然后再跟图像坐标系发生关系。

3、图像坐标系：分为图像物理坐标系和图像像素坐标系，以摄像机拍摄的二维图片为基准建立的坐标系，指物体在图片的位置。

图像物理坐标系(x,y)：其原点为透镜光轴与成像平面的交点，X 与Y 轴分别平行于摄像机坐标系的x与y 轴，是平面直角坐标系，单位为毫米。（X，Y）代表物体从摄像机坐标系到图像坐标系透视投影关系。

图像像素坐标系(u,v)：固定在图像上的以像素为单位的平面直角坐标系，其原点位于图像左上角, Xf，Yf平行于图像物理坐标系的X 和Y轴。对于数字图像，分别为行列方向。（u,v）则是实实在在的，我们能从摄像机得到的真实信息。

图像如下：

 

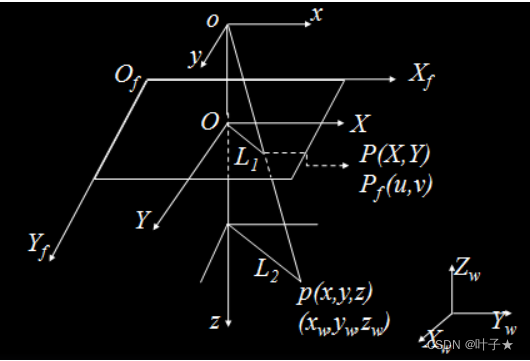
立体图：

 

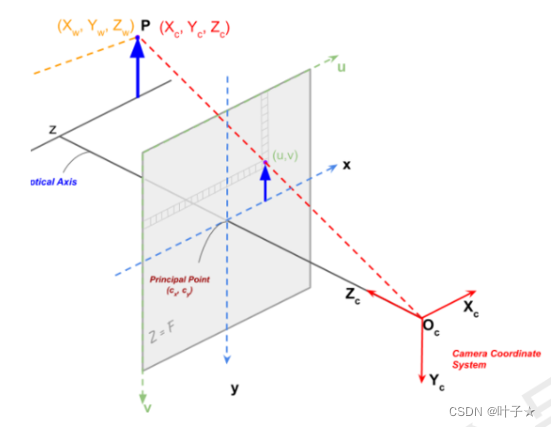
二、四大坐标系的坐标转换：

1、世界坐标转摄像机坐标：通过外参矩阵：旋转+平移（只要世界坐标和摄像机坐标相对位置关系发生改变，外参也会发生改变）

T是世界坐标系原点在摄像机坐标系中的坐标，矩阵R是正交旋转矩阵

2、摄像机坐标转像素坐标：先进行摄像机转图像物理坐标，再转为图像像素坐标，总结为内参矩阵（只与相机有关）

 

 以上转换流程图如下：

三、畸形模式

一、径向畸变

对于某些透镜，光线再远离透镜中心的地方比靠近中心的地方更加弯曲，产生'筒型'或者'鱼眼'现象，称为径向畸变。

一般来说，成像仪中心的径向畸变为0,越向近边缘移动，畸形越严重，径向畸变可以通过泰勒级数展示式来校正：

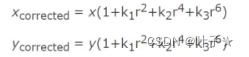
x,y是畸变点在成像仪上的原始位置，r为该点距离成像仪中心的距离，xcorreted,ycorreted是校正后的新位置。（对于一般的摄像机校正，通常使用泰勒级数中的前两项k1和k2就够了，畸变很打的摄像机，比如鱼眼透镜可以使用第三径向畸变项K3）

2、切向畸变 

当成像仪被粘贴在摄像机的时候，会存在一定的误差，是平面和透镜不完全平行，从而产生切向畸变，也就是说，如果一个矩形被投影到成像仪上时，可以会变成一个梯形，切向畸变可以通过如下公式校正，x,y,r,xcorreted,ycorreted参数跟以上意义一样

注意：x,y时图像物理坐标，不是图像像素坐标

图像描述如下：

径向畸变：桶形畸变，枕形畸变 （桶形x,y比实际要大，枕形刚好相反）

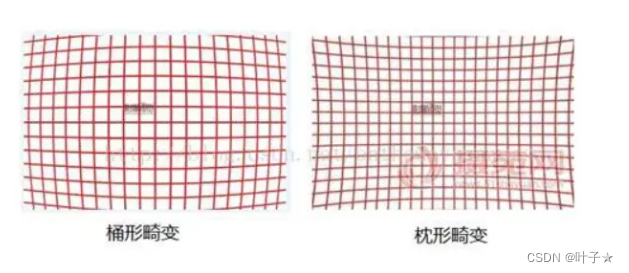
切向畸变： 

 

畸变系数：Distortioncoefficients=(k1k2p1p2k3)

要进行畸变矫正，必须知道畸变系数（求内参的目的，就是校正畸变和求外参 ），然后做畸变相反的操作，消除畸变 。

相机标定的最终目的：根据一组已知三维图像的世界坐标，以及不同角度拍摄获取的像素坐标，来计算出内存矩阵和外参矩阵，畸变参数。

标定之后就是消除畸变：由于每个镜头的畸变程度各不相同，通过相机标定可以校正镜头畸变矫正畸变，生成矫正后的图片；另一个是根据获得的图片进行重构三维场景。