哈希表

概念

为什么需要哈希表

静态查找表与动态查找表中，为了查找某关键字值等于某个值的记录，都要经过一系列的关键字进行比较，以确定待查记录的储存位置或查找失败，查找的时间总是与比较次数有关

什么是哈希表

哈希表，也叫散列表，英文Hash table，是根据关键码值而直接进行访问的数据结构。

哈希表的基本思想

• 将记录的存储位置与它的关键字之间建立一个确定的关系H，使每个关键字和唯一的存储位置对应。而这种关系H就是该哈希表的一个哈希函数。
• 在查找时，只需要根据对应关系计算出给定的关键字值H(k)，就可以得到记录的存储位置。这样，不经过比较，一次存取就能得到所查元素的查找方法。

哈希表相关术语

• 哈希函数：在记录的关键字与记录的存储地址之间建立的一种对应关系。
• 冲突： 若关键字不同而函数值相同，则称这两个关键字为“同义词”，并称这种现象为冲突。
• 哈希查找：利用哈希函数进行查找的过程。
• 装填因子：记表中添入记录数为$m$，表长度为$n$，则装填因子为$\alpha =\frac{m}{n}$

哈希表性质

• 哈希表实际上是以空间换取时间，它的查找的时间效率一般比其它方法高，但消耗空间资源
• 冲突一般不可避免，发生冲突的次数与表的装填程度呈正相关
• 哈希函数相同的情况下，处理冲突的方法不同，所得哈希表的平均查找长度也不同
• 线性探测再散列处理冲突容易造成记录的“二次聚集”，即使得本不是同义词的关键字又产生新的冲突
• 对开放定址处理冲突的哈希表而言，表长必须≥记录数
• 链地址处理冲突的哈希表不要求表长必须≥记录数，它的平均查找长度主要取决于哈希函数本身

构造哈希函数

构造哈希函数的方法有很多，但比较常用的有除留余数法、平方取中法等，需要根据数据的特性以及其它需要来选取

直接定址法

直接定址法取关键字本身或关键字某个线性函数作为哈希表的地址

设其关键字为$k$，那么线性表示的公式如下
$$H(k)=ak+b$$
该方法所得地址集合与关键字大小相等，不会发生冲突

适用情况：

• 给定的一组关键字为关键字集合中全体元素，若不是全体关键字，则必有某地址单元空闲

数字分析法

如果可能出现的关键字的数位相同，且取值事先知道，则可对关键字进行分析，取其中“分布均匀”的若干位或它们的组合作为哈希地址。

例如有80个记录，关键字为8位十进制数，哈希表表长为100，即地址范围为$[0,99]$

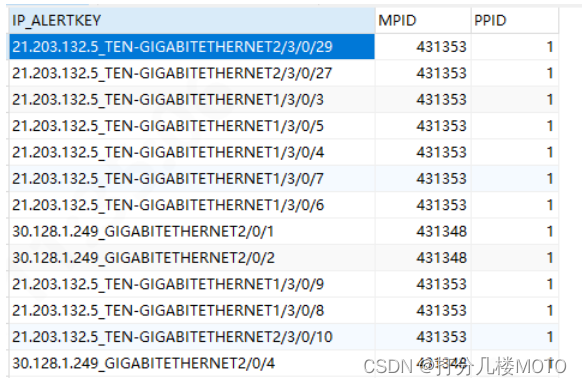
已知关键字如下图

对其进行分析，发现各个数字一号位置只取8，二号位置只取1，三号位置只取3、4，八号位置只取2、7、5。然而四、五、六、七号位置数字分布近乎随机。

故取四、五、六、七号位置数字任意两位或两位与另外两位叠加后得到的数字作为哈希地址。

适用情况：

• 关键字位数比哈希地址位数大，且可能出现的关键字事先知道的情况。

平方取中法

如果关键字的所有各位分布都不均匀，则可取关键字的平方值的中间若干位作为哈希表的地址。由于一个数的平方值的中间几位数受该数所有位影响，因此得到的哈希地址的分布均匀性要好一些，冲突要少一些。

例如，为标识符建立一个哈希表，假设标识符为一个字母或一个字母和数字。在计算机内用两位八进制数表示字母和数字，其利用平方取中法得到的关系如下图

适用情况：

• 适于不知道全部关键字情况
• 常用此法求取哈希函数

折叠法

若关键字的位数很多，且每一位上数字分布大致均匀，则可采用移位叠加或间界叠加。即将关键字分成若干部分，然后以它们的叠加和(舍去进位)作为哈希地址。

• 移位叠加是将分割后的每一部分的最低位对齐，然后相加
• 间界叠加是从一端向另一端沿分割界来回折叠，然后对齐相加

例如存在关键字0442205864，规定哈希地址位数为4，则利用上述两种叠加方法得到的地址可如下图

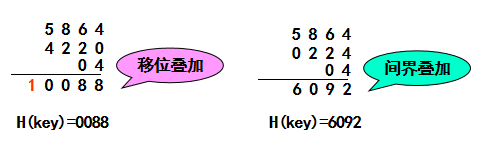
适用情况：

• 适于关键字位数很多，且每一位上数字分布大致均匀情况

除数留余法

该方法很简单，以关键字被某个数p除后所得余数作为哈希地址。

同样设k为关键字，p 为不大于表长的素数或不包含小于20的质因素的合数，公式如下
$$H(k)=k\mathrm{m}\mathrm{o}\mathrm{d}p$$
其中p的选取非常重要，如果选不好，则容易产生同义词。

随机数法

当关键字不等长时，可取关键字的某个伪随机函数值作为哈希地址。

公式如下：
$$H(k)=random(k)$$
适用情况：

• 适于关键字长度不等的情况

解决冲突

在上文中提到，使用某种方法构造出的哈希函数，对于不同关键字可能存在相同的函数值，所以这种情况就要解决冲突。

开放定址法

当冲突发生时，形成一个探查序列；沿此序列逐个地址探查，直到找到一个空位置（开放的地址），将发生冲突的记录放到该地址中。

公式如下：
$$\begin{gathered} H_i=(H(k)+d_i)\mathrm{m}\mathrm{o}\mathrm{d}m \\ i=1,2,3,...,k(k\le m-1) \end{gathered}$$
其中$k$为关键字，$m$为哈希表表长，$d_i$为增量序列

根据增量序列的取值不同，可以分为三类方法

• 线性探测再散列：$d_i=1,2,...,m-1$
• 二次探测再散列：$k<\frac{m}{2},d_i=1^2,-1^2,2^2,-2^2,...,\pm k^2$
• 伪随机探测再散列：$d_i$为伪随机数序列

例如表长为11的哈希表已经填有关键字为17、60、29的记录，其哈希函数为$H(k)=k\mathrm{m}\mathrm{o}\mathrm{d}11$，现将一关键字为38的新记录填入哈希表，利用上述三种方法得到的过程与结果分别如下

线性探测再散列

二次探测再散列

伪随机探测再散列

链地址法

将所有关键字为"同义词"的记录链接在一个线性链表中。此时的哈希表以"指针数组"的形式出现，数组内各个分量存储相应哈希地址的链表的头指针

再哈希法

构造若干个哈希函数，当发生冲突时，用另一个哈希函数计算另一个哈希地址，直至不发生冲突为止。

该方法需要预先设置一个哈希函数序列，另外它的计算时间相对增加了。

溢出区法

建立两个表，一个是基本表，另一个是溢出表（存放所有关键字和基本表中关键字冲突的记录，一旦冲突发生，就存入溢出表）。

平均找查长度ASL

找查长度

按照关系一次就找到元素位于哈希表中的位置，即成功找查长度记为1，如果第一次找查的位置不是相应的数字，则应该根据上文中的方法继续比较查找，并且次数依次加1。

如果上述操作最终没有找到该元素，则最后累计的长度为失败找查长度。

平均找查长度

ASL（Average Search Length），即平均查找长度，在查找运算中，由于所费时间在关键字的比较上，所以把平均需要和待查找值比较的关键字次数称为平均查找长度
$$ASL=\sum _{i=1}^n{p}_i{c}_i$$
其中$p_i$为第i个元素的概率；$c_i$是找到第i个元素的比较次数。

当然，平均找查长度有平均成功找查长度和平均失败找查长度

在讨论ASL时，我们一般各元素概率相等，即$p_i=\frac{1}{n}$

此时的平均找查长度为
$$ASL=\frac{1}{n}\sum _{i=1}^n{c}_i$$

几种方法的ASL

在等概率条件下，可以给出上文中提到的几种方法的平均成功找查长度和平局失败找查长度（此处不做证明）

线性探测再散列

平均成功找查长度：
$$S_{nl}\approx \frac{1}{2}(1+\frac{1}{1-\alpha })$$
平均失败找查长度：
$$U_{nl}\approx \frac{1}{2}(1+\frac{1}{(1-\alpha {)}^2})$$

随机探测再散列、二次探测再散列和再哈希

平均成功找查长度：
$$S_{nr}\approx -\frac{1}{\alpha }ln(1-\alpha )$$
平均失败找查长度：
$$U_{nr}\approx \frac{1}{1-\alpha }$$

链地址

平均成功找查长度：
$$S_{nc}\approx 1+\frac{\alpha }{2}$$
平均失败找查长度：
$$U_{nc}\approx \alpha +e^{-\alpha }$$

代码

关于哈希表的一个简单使用可以参考之前的文章

哈希排序算法 - 菜缤的世界 CairBin’s Blog