【POJ No. 3368】 最频繁值 Frequent values

北大OJ 题目地址

【题意】

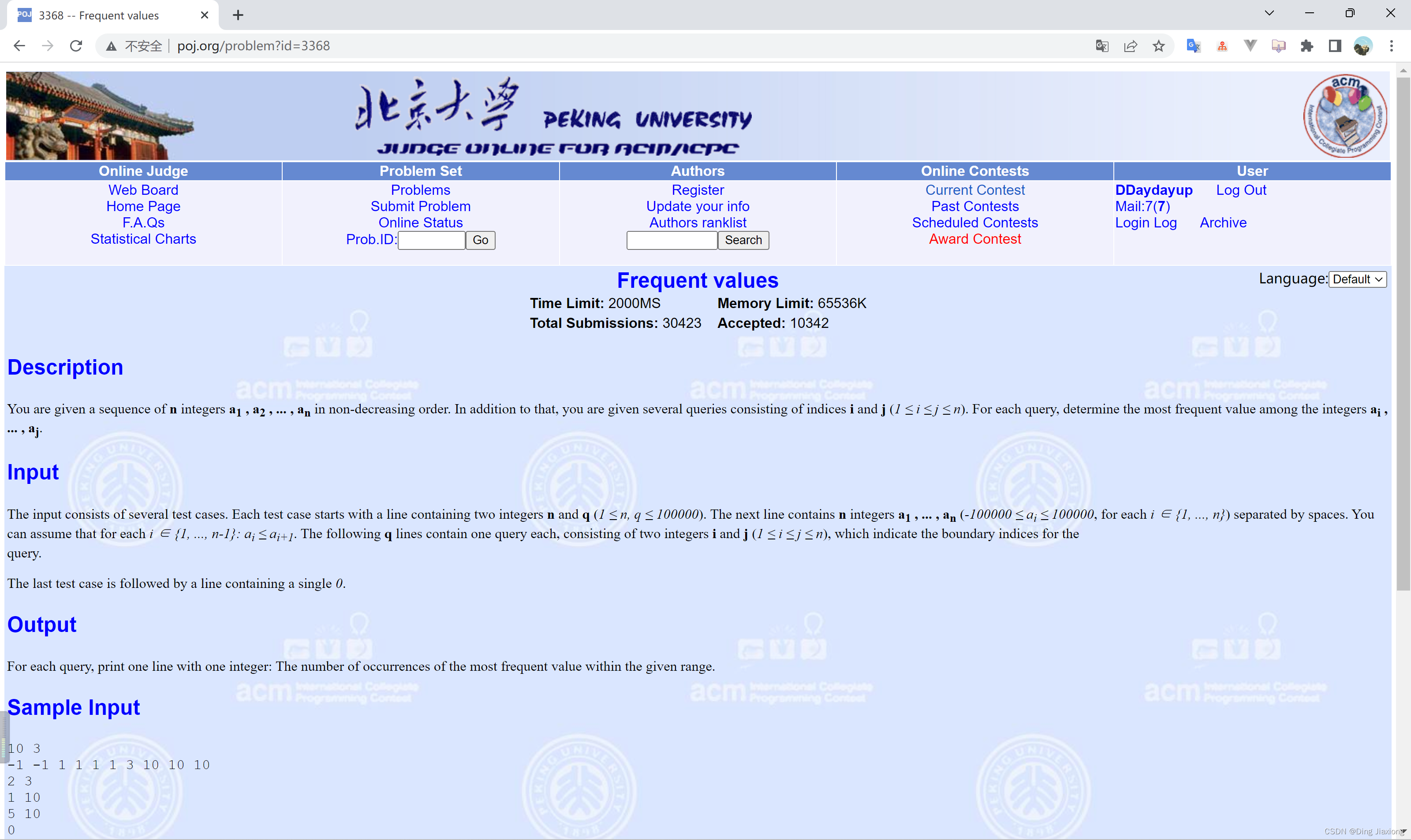
给定n 个整数的非递减序列a 1 , a 2 ,…, an ，对每个索引i 和j 组成的查询（1≤i ≤j ≤n ），都确定整数ai , …, aj 中的最频繁值（出现次数最多的值）。

【输入输出】

输入：

包含多个测试用例。每个测试用例都以两个整数n 和q（1≤n ，q ≤100000）的行开始。下一行包含n 个整数a 1 , …, an（-100000≤ai ≤100000，i ∈{1, …, n }）。对每个i ∈{1, …, n-1}，都满足ai ≤ai +1 。以下q 行，每行都包含一个查询，由两个整数i 和j 组成（1≤i ≤j ≤n ），表示查询的边界索引。在最后一个测试用例后跟一个包含单个0的行。

输出：

对每个查询，都单行输出一个整数，表示给定范围内最频繁值的出现次数。

【样例】

【思路分析】

这道题可以将元素的出现次数累计，然后进行区间最值查询，所以可以使用ST解决。

为提高求log的效率，首先用动态规划求出数据范围内所有数的log值，将其存储在数组lb[]中，使用时查询即可。F[i ][j ]表示[i , i +2 ^j -1]区间的最大值，区间长度为2 ^j 。

【算法设计】

① 求出数据范围内所有数的log值，将其存储在数组lb[]中。

② 非递减序列的相等元素一定相邻，将每个元素都和前面的元素比较，将重复次数累计并存入F[i ][0]中。

③ 创建ST。

④ 查询[l , r ]区间的最大值。若第l 个数和前一个数相等，则首先统计第l 个数在查询区间[l , r ]的出现次数，再查询剩余区间的最大值，两者再求最大值即可。

【举个栗子】

① 求出数据范围内所有数的log值，将其存储在数组lb[]中，规律如下。

• 2^i 和它的前一个数&运算必然是0，此时其log值比前一个数增加1。例如8的二进制为1000，7的二进制为111，两者与运算为0，log(8)比log(7)增加1。
• 除2 ^i 外，其他数和前一个数的与运算均不为0，其log值与前一个数相等。

首先，log[0]=-1。

1&0=0：log[1]=log[0]+1=0。

2&1=0：log[2]=log[1]+1=1。

3&2=2：log[3]=log[2]=1。

4&3=0：log[4]=log[3]+1=2。

5&4=4：log[5]=log[4]=2。

6&5=4：log[6]=log[5]=2。

7&6=6：log[7]=log[6]=2。

8&7=0：log[8]=log[7]+1=3。

……

② 将输入样例中元素的出现次数累计并存入F[i ][0]中。

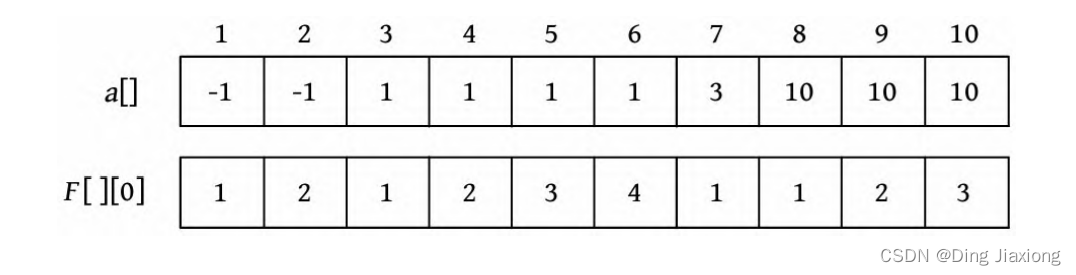
③ 创建ST。

④ 查询。2 3：查询[2, 3]区间最频繁值的出现次数。首先，t=l =2，因为a [2]=a [1]，t ++，即t =3；此时a [3]≠a [2]，t -l=1，RMQ(t , r )=RMQ(3, 3)=1，求两者的最大值，得到[2, 3]区间最频繁值的出现次数为1。

注意：不可以直接查询RMQ(2, 3)，为什么？

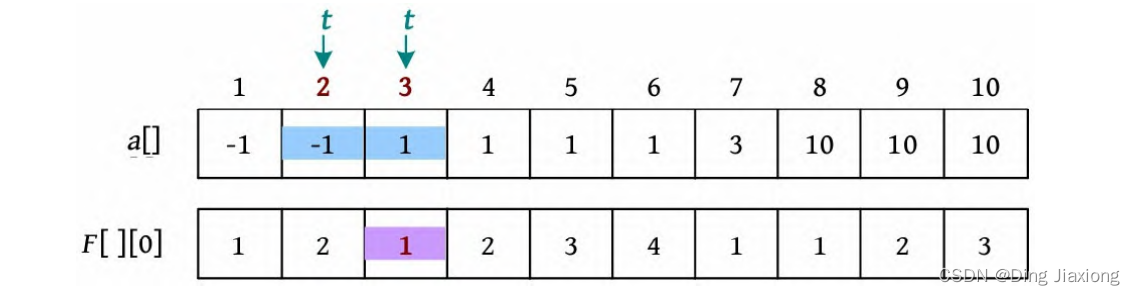
⑤ 查询。1 10：查询[1, 10]区间最频繁值的出现次数。首先，t =l =1，a [1]≠a [0]，t -l =0，RMQ(t , r )=RMQ(1, 10)=4，求两者的最大值，得到[1, 10]区间最频繁值的出现次数为4。

⑥ 查询。5 10：查询[5, 10]区间最频繁值的出现次数。首先，t =l =5，因为a [5]=a [4]，t ++，即t =6；a [6]=a [5]，t++，即t =7；此时a [7]≠a [6]，t -l =2，RMQ(t , r )=RMQ(7,10)=3，求两者的最大值，得到[5, 10]区间最频繁值的出现次数为3。

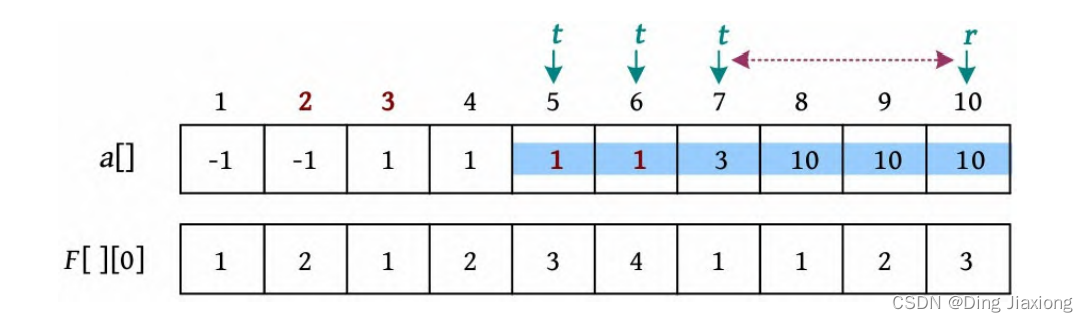
若直接查询RMQ(5, 10)=4，但是a [5]在[5, 10]区间的出现次数是2，则不是4。因此若a [l ]和前一个数a [l -1]相等，则需要先统计a[l ]在[l , r ]区间的出现次数，再查询剩余区间的最值，比较两者的最大值。

【算法实现】

#include<cstdio>
#include<algorithm>

using namespace std;
const int maxn=100010;

int a[maxn];//数据 
int lb[maxn];//存储log值 
int F[maxn][20];//F(i,j)表示区间[i，i+2^j-1]的最值，区间长度为2^j

void Initlog(){//求解所有log值,保存到数组lb[] 
	lb[0]=-1;
	for(int i=1;i<maxn;i++)
		lb[i]=(i&(i-1))?lb[i-1]:lb[i-1]+1;
}

void ST_create(int n){//每个测试用例n不同，因此做参数 
	for(int j=1;j<=lb[n];j++)
		for(int i=1;i<=n-(1<<j)+1;i++)//n-2^j+1
			F[i][j]=max(F[i][j-1],F[i+(1<<(j-1))][j-1]);		
}

int RMQ(int l,int r){//求区间[l..r]的最值差 
	if(l>r) return 0;
	int k=lb[r-l+1];
	return max(F[l][k],F[r-(1<<k)+1][k]);
}

int main(){
	
	int n,q,l,r;
	Initlog();
	while(~scanf("%d",&n)&&n){
		scanf("%d",&q);
		for(int i=1;i<=n;i++){//下标从1开始 
			scanf("%d",&a[i]);
			if(i==1){
				F[i][0]=1;
				continue;
			}	
			if(a[i]==a[i-1])
				F[i][0]=F[i-1][0]+1;
			else
				F[i][0]=1;
		}
		ST_create(n);
		for(int j=1;j<=q;j++){
			scanf("%d%d",&l,&r);
			int t=l;
			while(t<=r&&a[t]==a[t-1])
				t++;
			printf("%d\n",max(t-l,RMQ(t,r)));
		}
	}
	
	return 0;
}