目录
1 线性表
1.1 线性表的定义
1.2 线性表的基本操作
2 顺序表
2.1 顺序表定义
2.2 顺序表的实现
1.静态分配
2. 动态分配
3.顺序表的特点
2.3 顺序表操作
1.插入
2.删除
3.按位查找
4.按位查找
3 链表
3.1 单链表
1.定义
2. 插入和删除
3. 查找
4.单链表建立
3.2 双链表
1.建立
2.插入
3.删除
4.遍历
3.3 循环链表
1.循环单链表
2.循环双链表
3.循环双链表插入与删除
3.4 静态链表
3.5 顺序表与链表对比
1 线性表
1.1 线性表的定义

i表示元素在线性表中的位序,a1是表头元素,an是表尾元素
除表头元素外,每个元素有唯一直接前驱,除表尾元素外,每个元素有唯一直接后继
1.2 线性表的基本操作




2 顺序表
2.1 顺序表定义
用顺序存储的方式实现的线性表,将逻辑上相邻的元素存储在物理位置也相邻的存储单元中。
2.2 顺序表的实现
1.静态分配
用静态数组存放数据元素,静态空间大小固定
#define Maxsize 10
typedef struct{
int data[Maxsize]; // 静态数组存放数据元素
int length;
}SqList; // 顺序表的类型定义2. 动态分配
动态申请和释放内存空间。在C中使用malloc和free函数开拓并释放空间,C++中则使用new和delete。
#include <stdio.h>
#define Initsize 10 // 顺序表初始长度
typedef struct{
ElemType *data; // 指示动态分配数组的指针
int Maxsize; // 顺序表最大容量
int length; // 顺序表当前长度
}SqList; // 顺序表的类型定义该方法时间消耗大
3.顺序表的特点
·随机访问:在O(1)时间内找到第i个元素
·存储密度高,每个节点只存储数据元素
·拓展容量不便,动态分配时间复杂度高
·插入、删除操作不方便
2.3 顺序表操作
1.插入
ListInsert(&L,i,e):在表L中第i个位置上插入指定元素e。
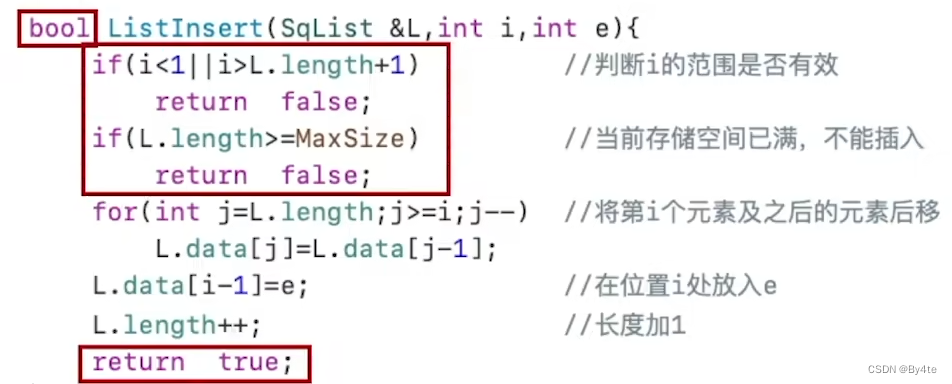
计算时间复杂度时,问题规模n = L.length
最好情况:插入表尾,i=n+1,循环0次;最好时间复杂度 = O(1)
最坏情况:插入表头,i=1,循环n次;最坏时间复杂度 = O(n)
平均情况:新元素插入到任何位置上概率相同,p = 1 / (n+1), 平均循环次数n / 2,平均时间复杂度 = O(n / 2) = O(n)
2.删除
ListDelete(&L,i,&e):删除表L中第i个位置上元素,并用e返回删除元素的值。

计算时间复杂度时,问题规模n = L.length
最好情况:删除表尾,i=n,循环0次;最好时间复杂度 = O(1)
最坏情况:插入表头,i=1,循环n-1次;最坏时间复杂度 = O(n)
平均情况:被删除元素在任何位置上概率相同,p = 1 / n , 平均循环次数(n-1) / 2,平均时间复杂度 = O(n)
3.按位查找
GetElem(L,i):获取表L中第i个位置元素的值。

时间复杂度:O(1)
4.按位查找
LocateElem(L,e):在表L中查找具有给定关键字值的元素。

计算时间复杂度时,问题规模n = L.length
最好情况:目标元素在表头,循环1次;最好时间复杂度 = O(1)
最坏情况:目标元素在表尾,循环n次;最坏时间复杂度 = O(n)
平均情况:目标元素出现在任何位置上概率相同,p = 1 / n , 平均循环次数(n+1) / 2,平均时间复杂度 = O(n)
3 链表
链式存储的线性表
3.1 单链表
1.定义
每个结点中存放数据元素和指向下一节点的指针

定义时需要包含数据域data与指针域*next。
包括带头结点和不太头结点两种实现方式
2. 插入和删除
·按位序插入(带头结点)
ListInsert(&L,i,e):在表L中第i个位置上插入指定元素e

·按位序插入(不带头结点)
ListInsert(&L,i,e):在表L中第i个位置上插入指定元素e
不带头结点需要更改头指针L的指向

·指定结点后插
bool InsertNextNode(L Node *p,Elemtype e)

·指定结点的前插
法一:bool InsertPriorNode(LinkList L,LNode *p,Elemtype e):给定头结点,遍历
法二:

·按位序删除(带头结点)
ListDelete(&L,i,&e):删除表L中第i个位置元素,并用e返回删除元素值
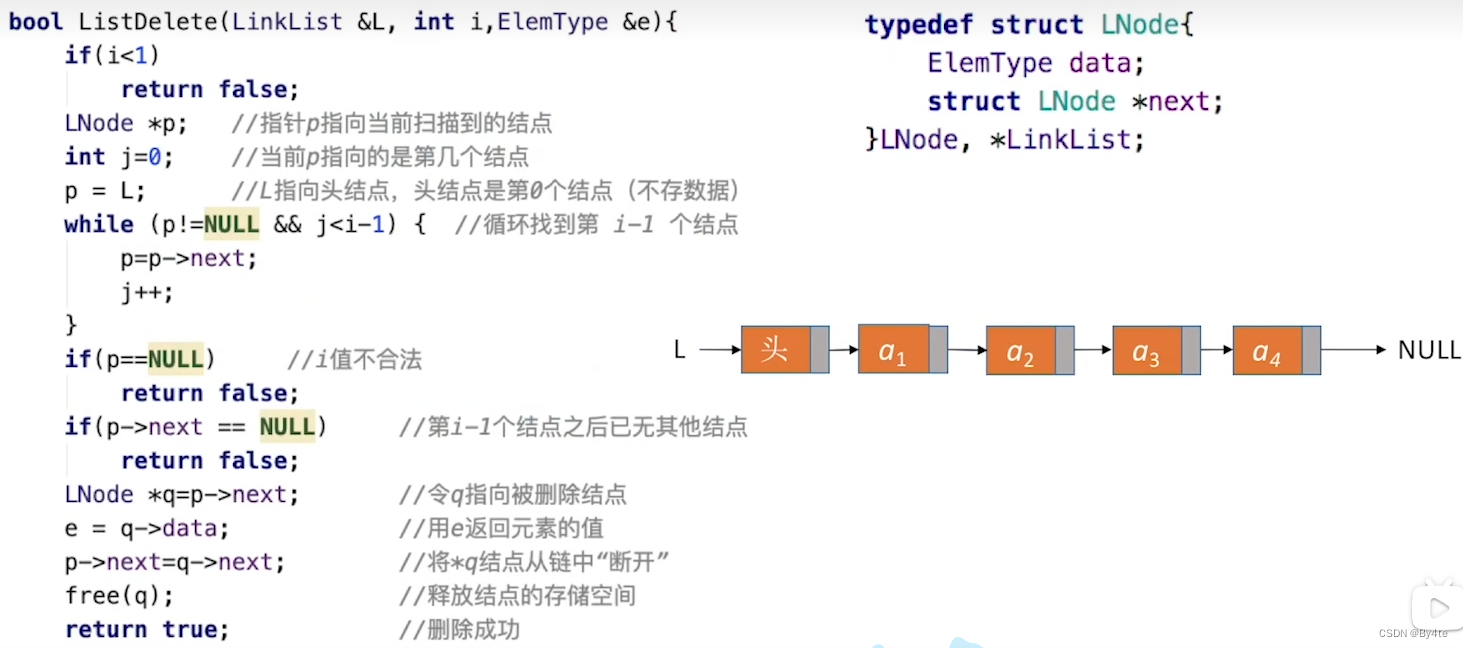
·删除指定结点
bool DeleteNode(LNode *p)

3. 查找
·按位查找
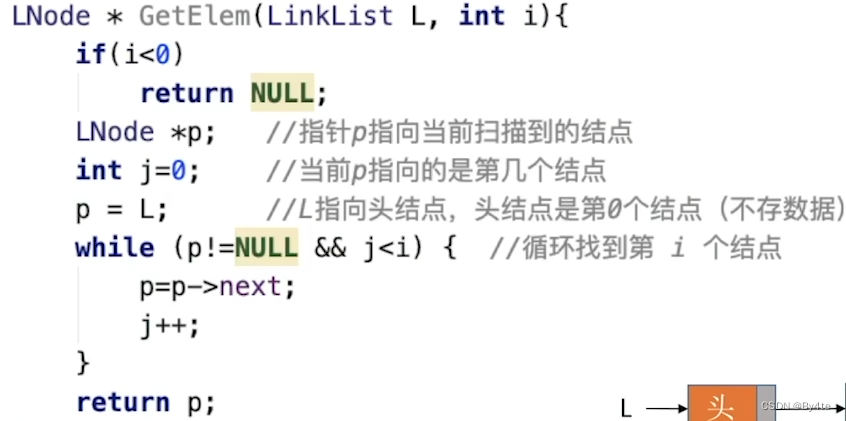
时间复杂度:O(n)
·按值查找

时间复杂度:O(n)
·求表长度

时间复杂度:O(n)
4.单链表建立
·尾插法

·头插法(可应用于链表的逆置)
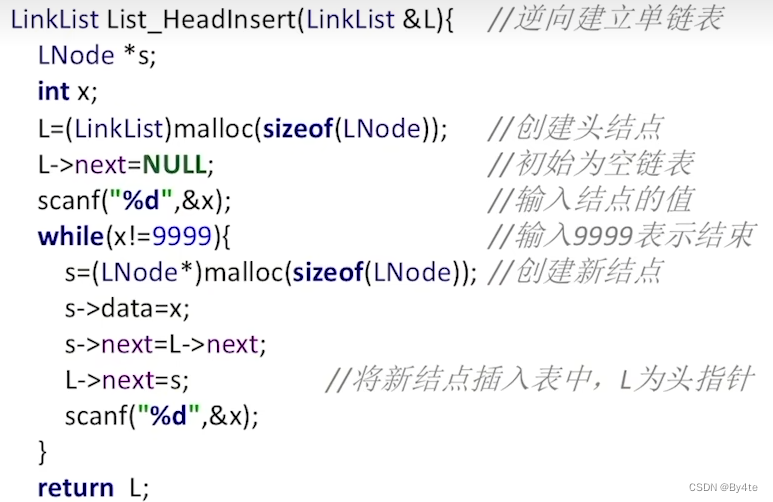
3.2 双链表
单链表无法逆向检索,可以使用双链表,增加一个前驱指针域
1.建立

2.插入

3.删除

4.遍历
后向遍历

前向遍历

双链表不可随机存取,按位查找、按值查找操作只能遍历,时间复杂度O(n)。
3.3 循环链表
1.循环单链表
表尾结点的next指针指向头结点
2.循环双链表
表头结点的prior指向表尾结点
表尾结点的next指向表头节点
3.循环双链表插入与删除
·插入

·删除

3.4 静态链表
单链表在内存中是离散的。静态链表将分配一整片连续的内存空间
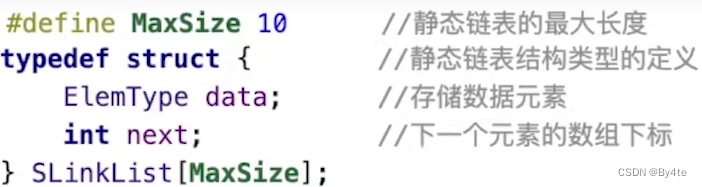
初始化:将a[0]对next设为-1,即指向NULL
3.5 顺序表与链表对比
1.逻辑结构
都属于线性表
2.存储结构
顺序表:支持随机存取、存储密度高;但连续空间分配不便,容量改变不易
链表::离散空间分配方便,容量改变较易;但不可随机存取,存储密度低
3.基本操作
顺序表:需要预分配空间,浪费内存;插入和删除需要移动元素,移动所需时间代价高;查找效率高
链表:只需分配头结点,便于拓展;插入和删除需要修改指针;
表上可预估,查找时多使用顺序表;表长难以预估,增删、扩容时多使用链表