泰勒展开式

简介

泰勒公式，也称泰勒展开式，可以用来在局部范围内近似复杂函数。

通俗的讲：
设有一个复杂的未知函数$f(x)$，我们想要知道它在某个范围$[a,b]$内的值，假设范围内有一个点$x_0$，已知$f(x_0)$。

我们无法通过$f(x)$直接求$f(x_0+\delta x)$的值，但如果已知其在某一点$x_0$的各阶导数值，泰勒公式可以利用这些导数值，以多项式形式在$x_0$附近来近似$f(x)$，求得$x_0$附近的值$f(x_0+\delta x)$。

定义

如果函数 $f(x)$ 在含 $x_0$ 的某个开区间 $(a,b)$ 内具有$(n+1)$ 阶导数，则对 $\forall x\in (a,b)$ ，有:
$$f(x)=\frac{f(x_0)}{0!}+\frac{f^{\prime }(x_0)}{1!}(x-x_0)+\dots +\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n+R_n(x)\text{\hspace{1em}(1)}$$

其中,
$R_n(x)=\frac{f^{(n+1)}(\xi )}{(n+1)!}(x-x_0{)}^{n+1}$，被称之为余项，代表近似函数和$f(x)$之间的误差， $\xi$ 为 $x_0$ 与 $x$ 之间的值。余项有几种表达方式，此为其中一种。

近似举例

假设有一个复杂的函数$f(x)$

• $x_0=0$时，$f(x_0)=1$
• $f^{(1)}(x_0)=f^{(3)}(x_0)$ = $f^{(5)}(x_0)=f^{(7)}(x_0)=0$
• $f^{(2)}(x_0)=f^{(6)}(x_0)=-1$
• $f^{(4)}(x_0)=f^{(8)}(x_0)=1$

我们用$P_n$来表示$n$阶的泰勒展开近似。

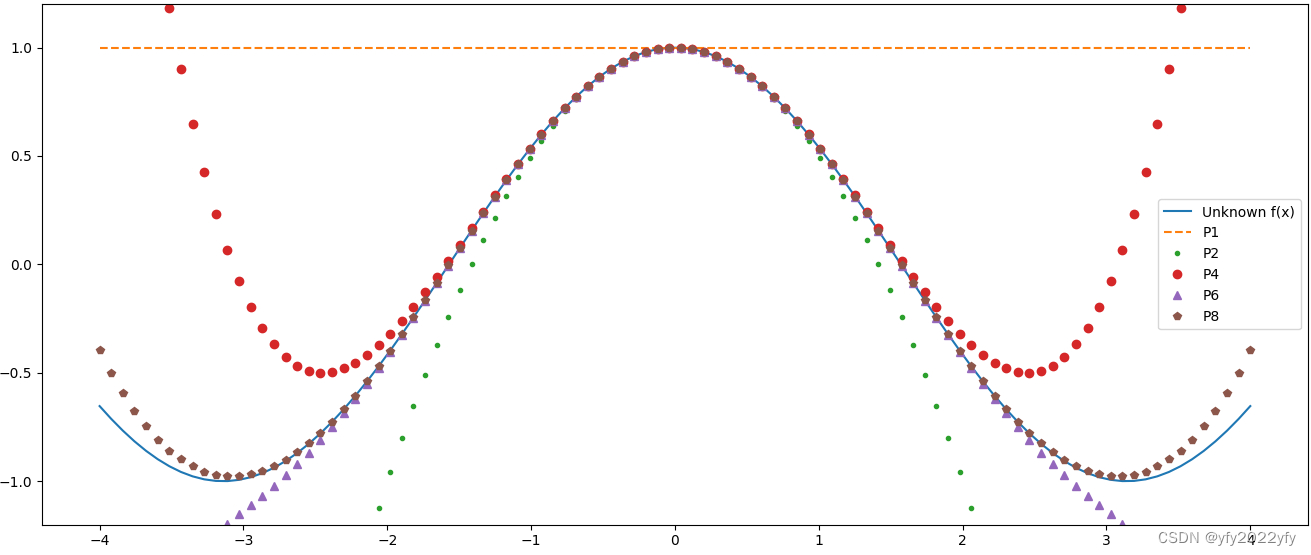
图中，P1,P2,P4,P6,P8 分别代表 $n=1,2,4,6,8$ 时的$P_i$ 函数的曲线。

可以很清楚的看到,当$n$ 越大，$P_i$和$f(x)$越近似

推导理解

设多项式$P_n(x)$：
$$P_n(x)=a_0+a_1(x-x_0)+a_2(x-x_0{)}^2+...+a_n(x-x_0{)}^n\text{\hspace{1em}(2)}$$
在$x_0$附近近似$f(x)$。

多项式 $P_n(x)$ 如果要和 $f(x)$ 在 $x_0$ 附近无限近似，则 $P_n(x)$ 和 $f(x)$ 曲线应该满足：

• 两曲线在$（x_0，f(x_0)）$处相交
• 进一步，两曲线在 $（x_0，f(x_0)）$ 处相切，即导数相同
• 进一步，两曲线在 $（x_0，f(x_0)）$ 处的导数变化一致，即二阶导数相同。
• …

即：
$$\begin{array}{rl}& P_n(x_0)=f(x_0)\\ & P_n^{(1)}(x_0)=f^{(1)}(x_0)=a_1\\ & P_n^{(2)}(x_0)=f^{(2)}(x_0)=2!a_2\\ & P_n^{(3)}(x_0)=f^{(3)}(x_0)=3!a_3\\ & ...\\ & P_n^{(n)}(x_0)=f^{(n)}(x_0)=n!a_n\end{array}\text{\hspace{1em}(3)}$$
将（2）中的 $a_0,a_1,a_2,...a_n$ 用（3）中的$f(x_0)$各阶导数替换，再用$R_n(x)$来表示两者间的误差，最终就得到了等式（1）。

参考

泰勒公式是怎么推导的？这篇文章告诉你！