实验九 数据微积分与方程数值求解
1.1实验目的
1.2实验内容
1.3流程图
1.4程序清单
1.5运行结果及分析
1.6实验的收获与体会
1.1实验目的
1,掌握求数值导数和数值积分的方法;
2,掌握代数方程数组求解的方法;
3,掌握多常微分方程数值求解的方法。
1.2实验内容


1.3流程图

1.4程序清单
%%
clc
clear
%% 1
clear;clc
x=1;i=1;
f=inline('det([x x.^2 x.^3;1+0*x 2*x 3*x.*x;0*x 2+0*x 6*x])');
while x<=3.01
g(i)=f(x);
i=i+1;
x=x+0.01;
end
g;
dx=diff(g)/0.01;
f1=dx(1)
f2=dx(101)
f3=dx(length(g)-1)
%% 2
clear
g1=inline('sqrt(cos(t.^2)+4*(sin(2.*t)).^2+1)');
g2=inline('log(1+x)./(1+x.^2)');
I1=quadl(g1,0,2*pi);
I2=quadl(g2,0,1);
%% 3
clear
A=[6 5 -2 5;
9 -1 4 -1;
3 4 2 -2;
3 -9 0 2];
b=[-4 13 1 11]';
x(:,1)=A\b;
[L,U]=lu(A);
x(:,2)=U\(L\b);
[Q,R]=qr(A);
x(:,3)=R\(Q\b);
%% 4
clear
A=[2 7 3 1;
3 5 2 2;
9 4 1 7];
b=[6 4 2]';
[x,y]= line_solution(A,b)
%% 5
clear
f=inline('3*x+sin(x)-exp(x)');
root_near=fzero(f,1.5);
X=fsolve('myfun',[1,1,1],optimset('Display','off'))
%% 6
clear
f=inline('(x^3+cos(x)+x*log10(x))/exp(x)');
[x,fval]=fminbnd(f,0,1);
[U,fmin]=fminsearch('fxy',[0,0]);
%% 7
clear
[x,y]=ode45('sys',[eps,10000],[eps,eps])
plot(x,y(:,1))
%% 8
clear
[T,Y]=ode45('rigid',[0 12],[0 1 1]);
plot(T,Y(:,1),'-',T,Y(:,2),'*',T,Y(:,3),'+');
相关函数:
function f = fj( x )
%UNTITLED3 此处显示有关此函数的摘要
% 此处显示详细说明
f=[x x^2 x^3;1 2*x 3*x^2; 0 2 6*x];
end
function [S_H, S_P] = line_solution(A,b)
% 输入参数A:系数矩阵
% 输入参数b:Ax=b的常数项列向量b
% S_H:齐次线性方程组的基础解系
% S_P:非齐次线性方程组的特解
if size(A,1) ~= length(b) %size(A,1)求矩阵的行数
error('输入数据错误,请重新输入!');
return;
else
B = [A,b]; %增广矩阵
rank_A = rank(A); %求系数矩阵的秩
rank_B = rank(B); %求增广矩阵的秩
if rank_A ~= rank_B %无解情况
disp('线性方程组无解!');
S_H = [];
S_P = [];
else if rank_B == size(A,2) %若增广矩阵的秩 = 未知量个数
%size(A,2)求矩阵的列数,相当于length(A)
disp('线性方程组有唯一解!');
S_P = A\b; %求唯一解
S_H = [];
else
disp('线性方程组有无穷解!');
S_H = null(A,'r');%求出齐次方程组的基础解系
S_P = A\b; %求非齐次方程组的特解
end
end
end
function F = myfun( X )
%UNTITLED6 此处显示有关此函数的摘要
% 此处显示详细说明
x=X(1);y=X(2);z=X(3);
F(1)=sin(x)+y^2+log(z);
F(2)=3*x+z^y-z^3+1;
F(3)=x+y+z-5;
end
function f = fxy( u )
%UNTITLED7 此处显示有关此函数的摘要
% 此处显示详细说明
x=u(1);y=u(2);
f=2*x^3+4*x*y^3-10*x*y+y^2;
end
function xdot =sys( x,y )
%UNTITLED8 此处显示有关此函数的摘要
% 此处显示详细说明
xdot=[y(2);(5*y(2)-y(1))/x];
end
function dy = rigid( t,y)
%UNTITLED10 此处显示有关此函数的摘要
% 此处显示详细说明
dy=zeros(3,1);
dy(1)=y(2)*y(3);
dy(2)=y(1)*y(3);
dy(3)=-0.51*y(2)*y(1);
end
1.5运行结果及分析
1.
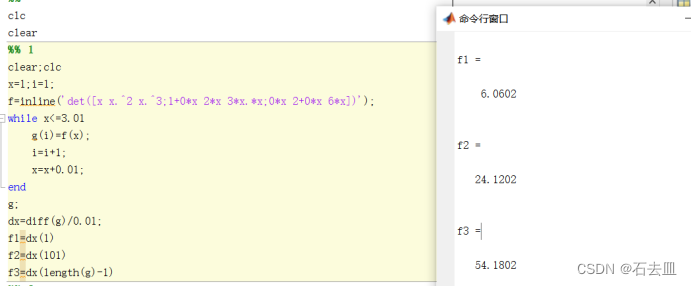
2.
3.
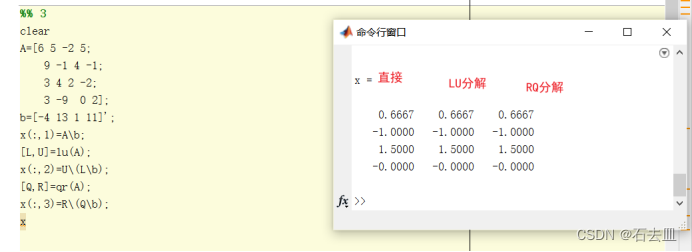
4.x的列向量乘以一个常数加上y就是通解。
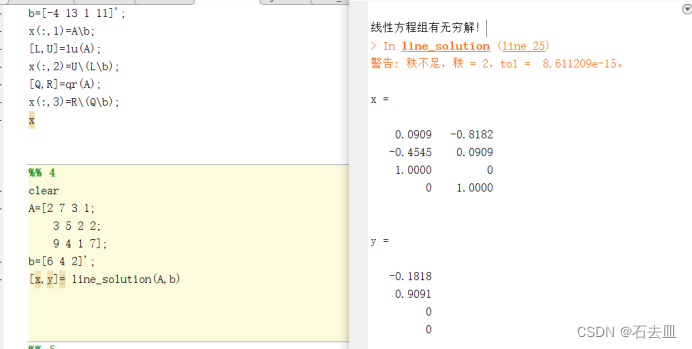
5.

6.

7.可以看出结果发散。
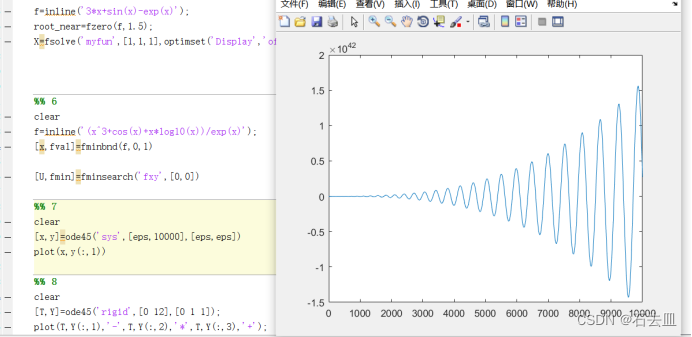
8.
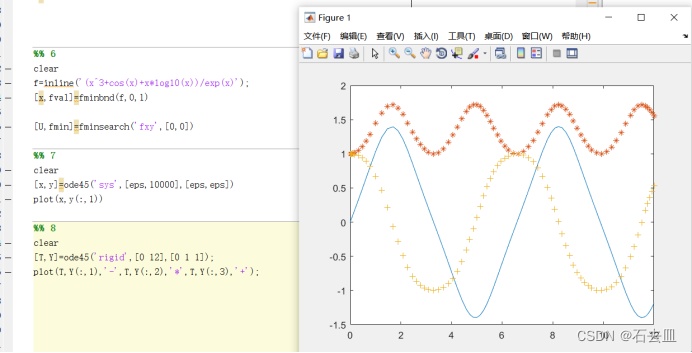
1.6实验的收获与体会
本次实验过后,我掌握了求数值导数和数值积分的方法和代数方程数组求解的方法,同时也掌握多常微分方程数值求解的方法。
数据微积分与方程数值求解是特别有用的工具。微积分的数值解法可以满足工程领域的需要,方程数值求解也可以满足一些需要。而往往工程问题都是不容易直接得出解析解的,那么这种情况,就需要使用数值解法来进行计算。虽然说有误差,但是这些误差都是实际践行中可以被接受和使用的。各种方法在matlab里面就只表现为一个函数,使用起来非常方便快捷。一些数值求解的过程,往往需要大规模的迭代计算,当然也可能因为结果发散,而无法迭代出一个收敛的结果,这也是很正常的一件事情,可能与系统结构相关。
总之,经过这次实验收获很大,对学习帮助很大。
源文档也可以有偿发(1块2米都可以),欢迎私聊!!!
欢迎向我赞赏:
https://smms.app/image/O2A1M9nzqYcG3Cr