【栈和队列的相互转换】

news2024/12/30 4:28:09

目录：

  • 前言
  • 一、 用队列实现栈
    • （一） 题目分析
      • 1.队列基本操作
      • 2.画图分析
      • 3.翻译图解
    • （二）整体代码
  • 二、用栈实现队列
    • （一） 题目分析
      • 1.栈基本操作
      • 2.画图分析
      • 3.翻译图解
    • （二）整体代码
  • 总结

前言

打怪升级：第6天
在这里插入图片描述

一、 用队列实现栈

  1. 用队列实现栈

题目描述：
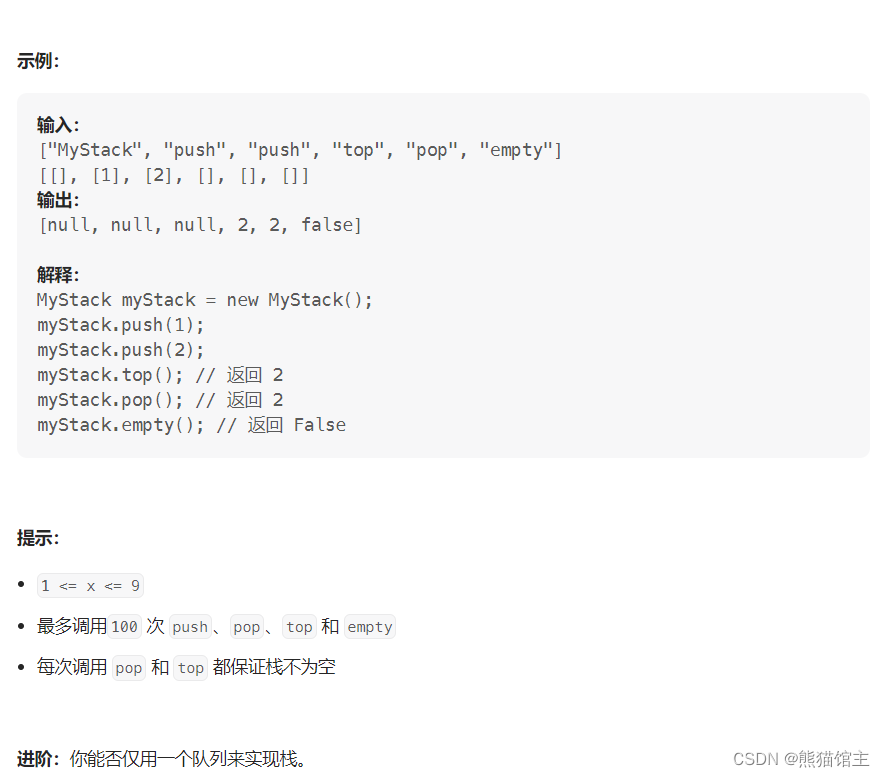
请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。
实现 MyStack 类：
void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。
注意：
你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。在这里插入图片描述

（一） 题目分析

此关卡要求我们使用两个队列来实现栈的操作，第一步就是需要有队列的基本操作函数，由于C语言没有c++中的stl库可以使用，我们就需要先写出队列的基本操作。

1.队列基本操作

代码如下：

typedef int QDataType;
// 链式结构：队列节点
typedef struct QListNode
{
	QDataType _data;
	struct QListNode* _next;
}QNode;

// 队列的结构 
typedef struct Queue
{
	int len;  // 记录节点的个数
	QNode* _front;
	QNode* _rear;
}Queue;

// 初始化队列 
void QueueInit(Queue* q)
{
	assert(q);
	q->len = 0;
	q->_front = q->_rear = NULL;
}
// 队尾入队列 
void QueuePush(Queue* q, QDataType data)
{
	QNode* tmp = (QNode*)malloc(sizeof(QNode));
	if (tmp == NULL)
		exit(-1);

	tmp->_data = data;
	tmp->_next = NULL;
	q->len++;
	if (q->_front == NULL) // 空队列
	{
		q->_front = q->_rear = tmp;
	}
	else
	{
		q->_rear->_next = tmp;
		q->_rear = q->_rear->_next;
	}
}
// 队头出队列 
void QueuePop(Queue* q)
{
	assert(q);

	if (QueueEmpty(q))
		exit(-1);

	QNode* next = q->_front->_next;
	free(q->_front);
	q->_front = next;
	if(q->_front == NULL)  // 队列只剩下一个数据，删除之后rear成为野指针
	q->_rear = q->_front;
	q->len--;
}
// 获取队列头部元素 
QDataType QueueFront(Queue* q)
{
	assert(q);

	if (QueueEmpty(q))
		exit(-1);

	return q->_front->_data;
}
// 获取队列队尾元素 
QDataType QueueBack(Queue* q)
{
	assert(q);

	if (QueueEmpty(q))
		exit(-1);

	return q->_rear->_data;
}
// 获取队列中有效元素个数 
int QueueSize(Queue* q)
{
	assert(q);

	return q->len;
}
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q)
{
	assert(q);

	return q->len == 0;
}
// 销毁队列 
void QueueDestroy(Queue* q)
{
	assert(q);

	QNode* cur = q->_front;
	while (cur)
	{
		QNode* next = cur->_next;
		free(cur);
		cur = next;
	}
}

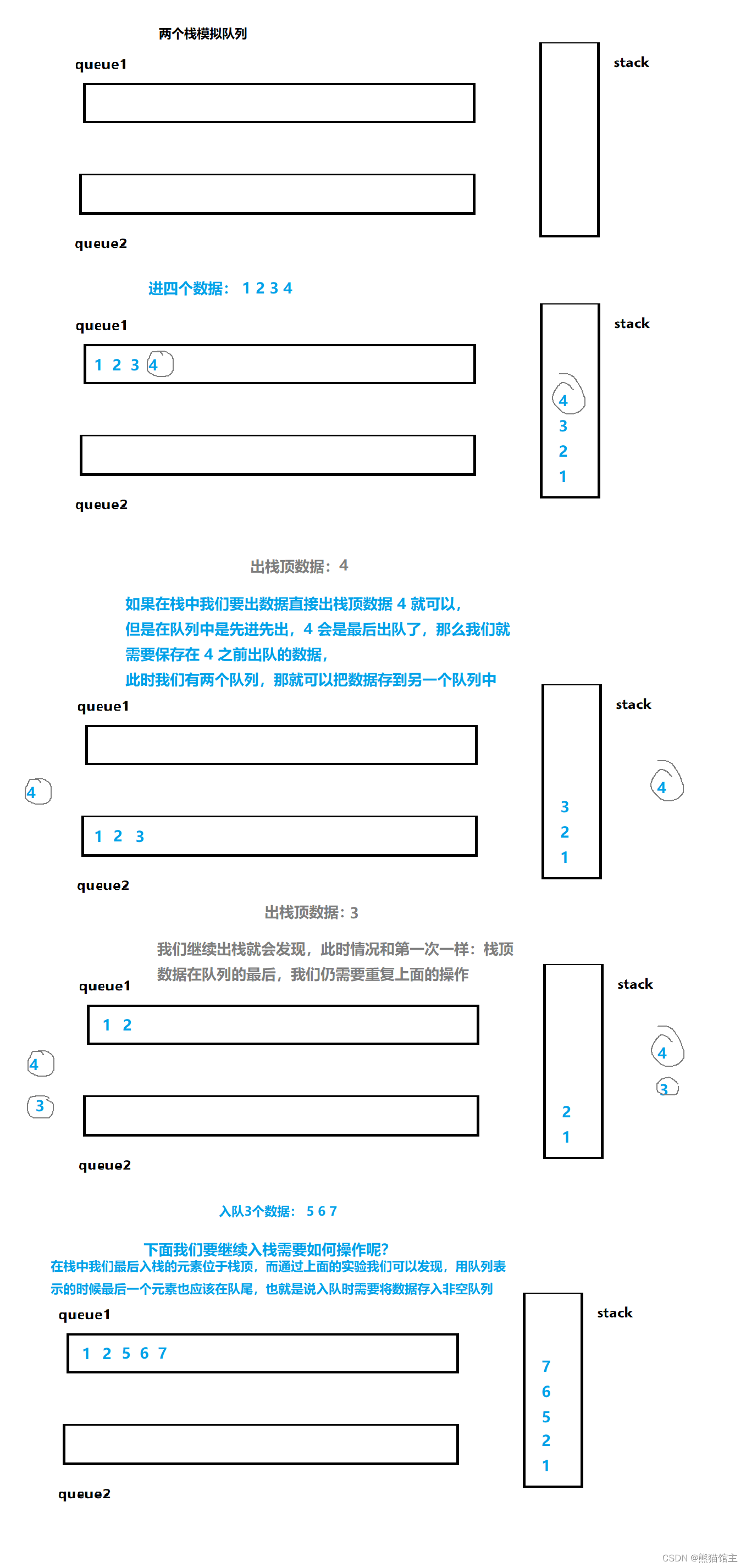
2.画图分析

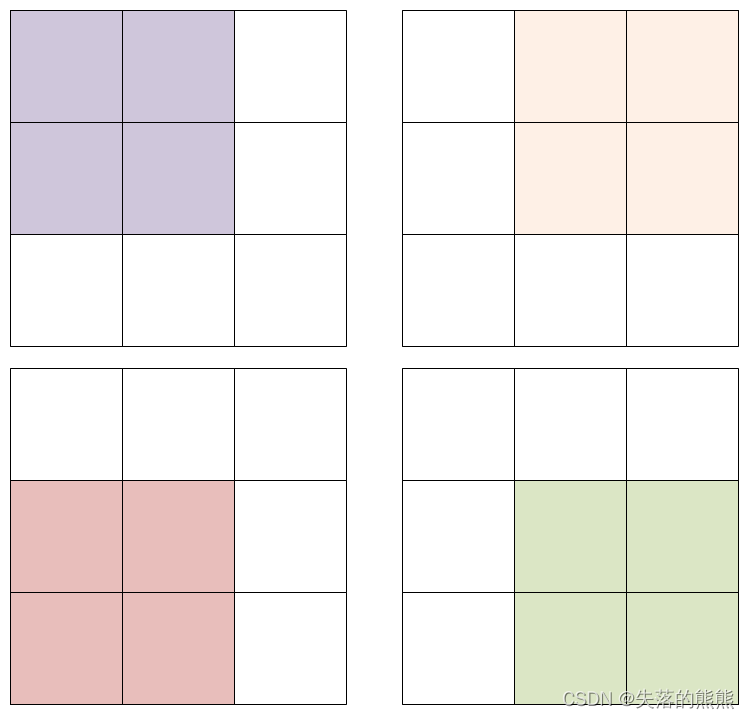
栈的特点是“后进先出”而队列的特点是“先进先出”，我们想要使用队列模拟栈就需要通过实验找出它们之间的转换关系，
如下图：
在这里插入图片描述
出栈操作视频解析：

用队列模拟出栈--1


用队列模拟出栈--2

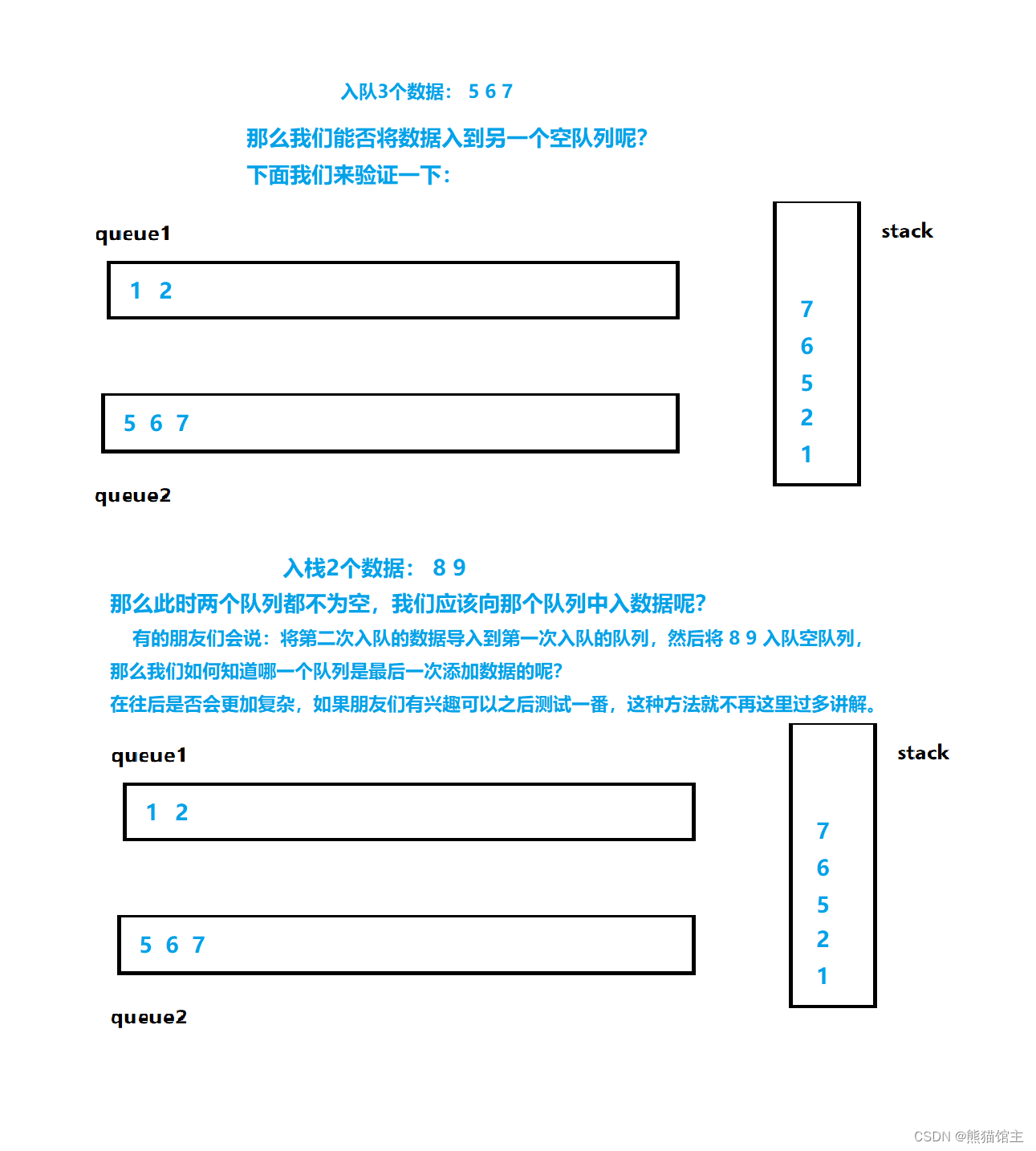
另一个入栈操作：（不推荐）
在这里插入图片描述

3.翻译图解

题目已经明说：在执行pop和top操作时队列不为空，那么我们判不判断这个特殊情况都无所谓了，不过我还是建议大家判断一下，培养良好的做题习惯。
示例：

typedef struct {
	Queue q1;
	Queue q2;
} MyStack; // 栈中元素为两个队列

MyStack* myStackCreate() {
	MyStack* s = (MyStack*)malloc(sizeof(MyStack));
	QueueInit(&s->q1);
	QueueInit(&s->q2);

	return s;
}

void myStackPush(MyStack* obj, int x) {  // 数据需要进到非空队列
	Queue* nonemp = &obj->q1;  //  我们不知道哪一个为非空队列，那就先假设是第一个
	if (!QueueEmpty(&obj->q2))
		nonemp = &obj->q2;

	QueuePush(nonemp, x);
}

int myStackPop(MyStack* obj) {
	Queue* nonemp = &obj->q1;
	Queue* emp = &obj->q2;

	if (!QueueEmpty(&obj->q2))
	{
		nonemp = &obj->q2;
		emp = &obj->q1;
	}

	while (QueueSize(nonemp) > 1) // 非空队列中只剩一个数据时，它就是我们要删除的栈顶数据
	{
		QueuePush(emp, QueueFront(nonemp));
		QueuePop(nonemp);
	}

	QDataType tmp = QueueFront(nonemp); // 记录队尾数据
	QueuePop(nonemp);

	return tmp;
}

int myStackTop(MyStack* obj) {
	Queue* nonemp = &obj->q1;
	if (!QueueEmpty(&obj->q2))
		nonemp = &obj->q2;

	return QueueBack(nonemp);
}

bool myStackEmpty(MyStack* obj) {

	return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);  //两个队列都为空才说明栈为空
}

void myStackFree(MyStack* obj) {
	QueueDestroy(&obj->q1);
	QueueDestroy(&obj->q2);
	free(obj);
}

（二）整体代码

示例：

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

typedef int QDataType;
// 链式结构：表示队列 
typedef struct QListNode
{
	QDataType _data;
	struct QListNode* _next;
}QNode;

// 队列的结构 
typedef struct Queue
{
	int len;
	QNode* _front;
	QNode* _rear;
}Queue;

// 初始化队列 
void QueueInit(Queue* q)
{
	assert(q);
	q->len = 0;
	q->_front = q->_rear = NULL;
}
// 队尾入队列 
void QueuePush(Queue* q, QDataType data)
{
	QNode* tmp = (QNode*)malloc(sizeof(QNode));
	if (tmp == NULL)
		exit(-1);

	tmp->_data = data;
	tmp->_next = NULL;
	q->len++;
	if (q->_front == NULL) // 空队列
	{
		q->_front = q->_rear = tmp;
	}
	else
	{
		q->_rear->_next = tmp;
		q->_rear = q->_rear->_next;
	}
}
// 队头出队列 
void QueuePop(Queue* q)
{
	assert(q);

	if (QueueEmpty(q))
		exit(-1);

	QNode* next = q->_front->_next;
	free(q->_front);
	q->_front = next;
	q->len--;
}
// 获取队列头部元素 
QDataType QueueFront(Queue* q)
{
	assert(q);

	if (QueueEmpty(q))
		exit(-1);

	return q->_front->_data;
}
// 获取队列队尾元素 
QDataType QueueBack(Queue* q)
{
	assert(q);

	if (QueueEmpty(q))
		exit(-1);

	return q->_rear->_data;
}
// 获取队列中有效元素个数 
int QueueSize(Queue* q)
{
	assert(q);

	return q->len;
}
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q)
{
	assert(q);

	return q->len == 0;
}
// 销毁队列 
void QueueDestroy(Queue* q)
{
	assert(q);

	QNode* cur = q->_front;
	while (cur)
	{
		QNode* next = cur->_next;
		free(cur);
		cur = next;
	}
}





typedef struct {
	Queue q1;
	Queue q2;
} MyStack;

MyStack* myStackCreate() {
	MyStack* s = (MyStack*)malloc(sizeof(MyStack));
	QueueInit(&s->q1);
	QueueInit(&s->q2);

	return s;
}

void myStackPush(MyStack* obj, int x) {  // 数据需要进到非空队列
	Queue* nonemp = &obj->q1;
	if (!QueueEmpty(&obj->q2))
		nonemp = &obj->q2;

	QueuePush(nonemp, x);
}

int myStackPop(MyStack* obj) {
	Queue* nonemp = &obj->q1;
	Queue* emp = &obj->q2;

	if (!QueueEmpty(&obj->q2))
	{
		nonemp = &obj->q2;
		emp = &obj->q1;
	}

	while (QueueSize(nonemp) > 1)
	{
		QueuePush(emp, QueueFront(nonemp));
		QueuePop(nonemp);
	}

	QDataType tmp = QueueFront(nonemp); // 记录队尾数据
	QueuePop(nonemp);

	return tmp;
}

int myStackTop(MyStack* obj) {
	Queue* nonemp = &obj->q1;
	if (!QueueEmpty(&obj->q2))
		nonemp = &obj->q2;

	return QueueBack(nonemp);
}

bool myStackEmpty(MyStack* obj) {

	return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}

void myStackFree(MyStack* obj) {
	QueueDestroy(&obj->q1);
	QueueDestroy(&obj->q2);
	free(obj);
}

提交结果：在这里插入图片描述

补充：题目下方的进阶要求->使用一个队列模拟实现栈
提示：循环队列

二、用栈实现队列

  1. 用栈实现队列

题目描述：
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：
实现 MyQueue 类：
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false
说明：
你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。
在这里插入图片描述

（一） 题目分析

此关卡通关要求为：使用两个栈来模拟实现队列完成基本操作。
那么第一步同上：写出栈的基本操作

1.栈基本操作

代码如下：

// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
	STDataType* _a;
	int _top;		// 栈顶
	int _capacity;  // 容量 
}Stack;

// 初始化栈 
void StackInit(Stack* ps)
{
	assert(ps);

	ps->_a = (STDataType*)malloc(sizeof(STDataType) * 3);
	ps->_top = 0;
	ps->_capacity = 3;
}
// 入栈 
void StackPush(Stack* ps, STDataType data)
{
	assert(ps);

	if (ps->_top == ps->_capacity)
	{
		STDataType* tmp = realloc(ps->_a, sizeof(STDataType) * ps->_capacity * 2);
		assert(tmp);

		ps->_a = tmp;
		ps->_capacity *= 2;
	}

	ps->_a[ps->_top++] = data;
}
// 出栈 
void StackPop(Stack* ps)
{
	assert(ps);

	if (StackEmpty(ps))
		exit(-1);

	ps->_top--;
}
// 获取栈顶元素 
STDataType StackTop(Stack* ps)
{
	assert(ps);

	if (StackEmpty(ps))
		exit(-1);

	return ps->_a[ps->_top - 1];
}
// 获取栈中有效元素个数 
int StackSize(Stack* ps)
{
	assert(ps);

	return ps->_top;
}
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
int StackEmpty(Stack* ps)
{
	assert(ps);

	return ps->_top == 0;
}
// 销毁栈 
void StackDestroy(Stack* ps)
{
	assert(ps);

	free(ps->_a);
	ps->_a = NULL;
	ps->_top = ps->_capacity = 0;
}

2.画图分析

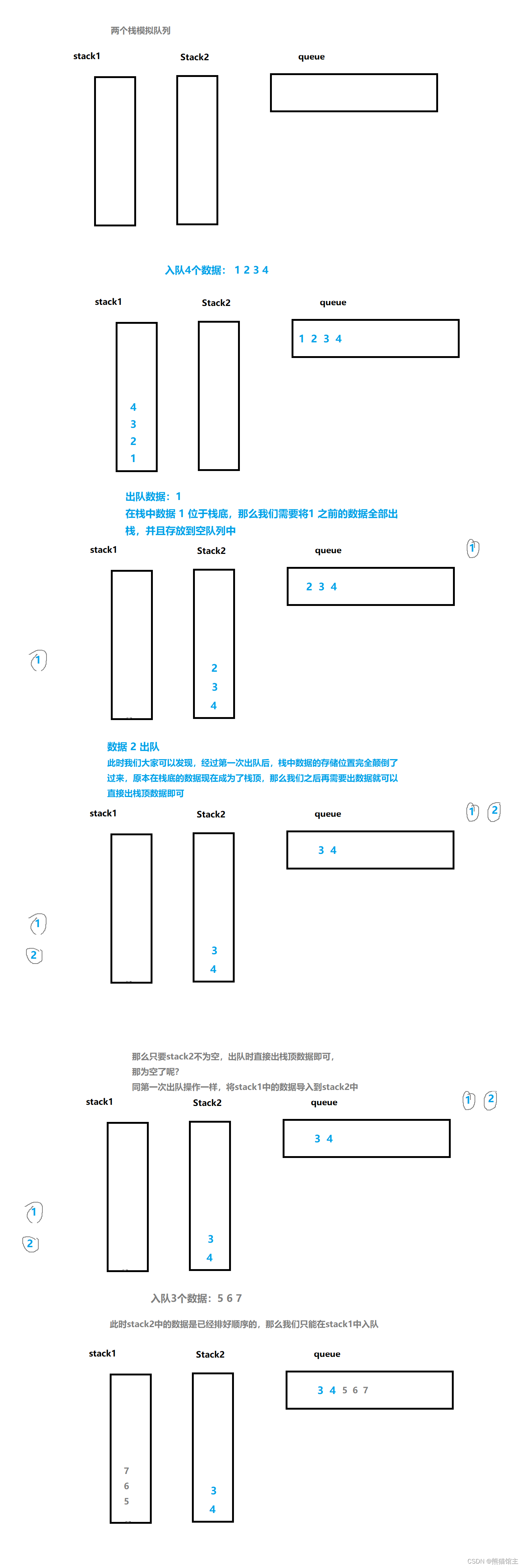
栈的特点是后进先出，队列的特点为先进先出，下面我们通过画图来找到它们之间的转换关系
在这里插入图片描述
视频解析：

用栈模拟出队--1


用栈模拟出队--2

3.翻译图解

代码如下：

typedef struct {
	Stack instack;
	Stack outstack;
} MyQueue; // 两个栈模拟队列，从画图我们可以看出一个栈是专门用来入数据的，另一个是用来出数据的


MyQueue* myQueueCreate() {

	MyQueue* q = (MyQueue*)malloc(sizeof(MyQueue));
	StackInit(&q->instack);
	StackInit(&q->outstack);

	return q;
}

void myQueuePush(MyQueue* obj, int x) {

	StackPush(&obj->instack, x);
}

int myQueuePeek(MyQueue* obj) {
	if (StackEmpty(&obj->outstack))
	{
		while (!StackEmpty(&obj->instack))
		{
			StackPush(&obj->outstack, StackTop(&obj->instack));
			StackPop(&obj->instack);
		}
	}

	return StackTop(&obj->outstack);
}

int myQueuePop(MyQueue* obj) {

	STDataType con = myQueuePeek(obj);

	StackPop(&obj->outstack);

	return con;
}

bool myQueueEmpty(MyQueue* obj) {

	return StackEmpty(&obj->instack) && StackEmpty(&obj->outstack);
}

void myQueueFree(MyQueue* obj) {

	StackDestroy(&obj->instack);
	StackDestroy(&obj->outstack);
	free(obj);
}

（二）整体代码

示例：


// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
	STDataType* _a;
	int _top;		// 栈顶
	int _capacity;  // 容量 
}Stack;

// 初始化栈 
void StackInit(Stack* ps)
{
	assert(ps);

	ps->_a = (STDataType*)malloc(sizeof(STDataType) * 3);
	ps->_top = 0;
	ps->_capacity = 3;
}
// 入栈 
void StackPush(Stack* ps, STDataType data)
{
	assert(ps);

	if (ps->_top == ps->_capacity)
	{
		STDataType* tmp = realloc(ps->_a, sizeof(STDataType) * ps->_capacity * 2);
		assert(tmp);

		ps->_a = tmp;
		ps->_capacity *= 2;
	}

	ps->_a[ps->_top++] = data;
}
// 出栈 
void StackPop(Stack* ps)
{
	assert(ps);

	if (StackEmpty(ps))
		exit(-1);

	ps->_top--;
}
// 获取栈顶元素 
STDataType StackTop(Stack* ps)
{
	assert(ps);

	if (StackEmpty(ps))
		exit(-1);

	return ps->_a[ps->_top - 1];
}
// 获取栈中有效元素个数 
int StackSize(Stack* ps)
{
	assert(ps);

	return ps->_top;
}
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
int StackEmpty(Stack* ps)
{
	assert(ps);

	return ps->_top == 0;
}
// 销毁栈 
void StackDestroy(Stack* ps)
{
	assert(ps);

	free(ps->_a);
	ps->_a = NULL;
	ps->_top = ps->_capacity = 0;
}


typedef struct {
	Stack instack;
	Stack outstack;
} MyQueue;


MyQueue* myQueueCreate() {

	MyQueue* q = (MyQueue*)malloc(sizeof(MyQueue));
	StackInit(&q->instack);
	StackInit(&q->outstack);

	return q;
}

void myQueuePush(MyQueue* obj, int x) {

	StackPush(&obj->instack, x);
}

int myQueuePeek(MyQueue* obj) {
	if (StackEmpty(&obj->outstack))
	{
		while (!StackEmpty(&obj->instack))
		{
			StackPush(&obj->outstack, StackTop(&obj->instack));
			StackPop(&obj->instack);
		}
	}
	
	return StackTop(&obj->outstack);
}

int myQueuePop(MyQueue* obj) {

	STDataType con = myQueuePeek(obj);

	StackPop(&obj->outstack);

	return con;
}

bool myQueueEmpty(MyQueue* obj) {

	return StackEmpty(&obj->instack) && StackEmpty(&obj->outstack);
}

void myQueueFree(MyQueue* obj) {

	StackDestroy(&obj->instack);
	StackDestroy(&obj->outstack);
	free(obj);
}

提交结果：
在这里插入图片描述

补充：题目下方的进阶要求->实现每个操作均摊时间复杂度为 O(1) 的队列，
那么细心的朋友应该能发现有可能出现O(n)时间复杂度的地方就是计算队列的元素个数上，而我们这里使用并没有使用这些操作，这里我们其实已经达到了进阶要求。

总结

好了朋友们，以上就是栈和队列相互转换使用的例题了，我想当我们打过了这两关后我们对栈和队列的特点和用法理解都会上一个新的台阶。
如果有什么疑问或者建议都可以在评论区留言，感谢大家对在这里插入图片描述的支持。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/25504.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

wy的leetcode刷题记录_Day47

wy的leetcode刷题记录_Day47

wy的leetcode刷题记录_Day47 声明 本文章的所有题目信息都来源于leetcode 如有侵权请联系我删掉! 时间&#xff1a;2022-11-20 前言 补 目录wy的leetcode刷题记录_Day47声明前言799. 香槟塔题目介绍思路代码收获105. 从前序与中序遍历序列构造二叉树题目介绍思路代码收获79…
阅读更多...
优思学院｜精益六西格玛的成本效益怎么样？

优思学院｜精益六西格玛的成本效益怎么样？

所有精益六西格玛的实施都以项目工作为中心&#xff0c;因此可以用投资回报率&#xff08;ROI&#xff09;确定成本效益。项目可以集中在通过改善营收或降低成本&#xff08;或两者&#xff09;来提高净利润。 它们也可以侧重于通过减少资产&#xff08;通常是库存或应收账款&…
阅读更多...
迅为IMX8M开发板2gst-inspect-1.0测试

迅为IMX8M开发板2gst-inspect-1.0测试

gstreamer 开发中&#xff0c;一般开发思路为&#xff1a;寻找命令行实现--命令行验证--将命令行集成到代码中---代码工程 化。当然如果你要代码更优雅一点&#xff0c;可以用命令行用对应的 API 来实现。本节来总结一下 gstreamer 的常用 使用过程。 gst-inspect 可以查看插件…
阅读更多...
新鲜出炉，Linux眼花缭乱的小寄巧

新鲜出炉，Linux眼花缭乱的小寄巧

14天学习训练营导师课程&#xff1a; 互联网老辛《 符合学习规律的超详细linux实战快速入门》 努力是为了不平庸~ 学习有些时候是枯燥的&#xff0c;但收获的快乐是加倍的&#xff0c;欢迎记录下你的那些努力时刻&#xff08;学习知识点/题解/项目实操/遇到的bug/等等&#xf…
阅读更多...
MySQL_数据库的约束

MySQL_数据库的约束

文章目录 1. NULL约束 2. UNIQUE(唯一约束) 3. DEFAULT(默认值约束) 4. PRIMARY KEY(主键约束) 5. FOREIGN KEY(外键约束) 数据库的约束就是关系型数据库给我们提供的一种"校验数据"合法性的机制 1. NULL约束 创建表时,可以指定某列不为空 create table stud…
阅读更多...
MindFusion Scheduler for JavaScript 2.0 Crack

MindFusion Scheduler for JavaScript 2.0 Crack

用纯 JAVASCRIPT 编写的交互式调度库--MindFusion Scheduler for JavaScript MindFusion 为所有需要呈现交互式时间表、活动日程或约会日历的应用程序提供了完整的解决方案。完全响应、高度可定制且易于集成的 JavaScript 调度库&#xff0c;您可以根据需要快速编程。 本土化 本…
阅读更多...
Centos7 linux 中 防火墙操作命令及SSH远程连接

Centos7 linux 中 防火墙操作命令及SSH远程连接

文章目录查看防火墙状态开启防火墙关闭防火墙查看对外开放的端口状态对外开发端口SSH 工具远程连接VMware 虚拟机查看防火墙状态 systemctl status firewalld开启防火墙 systemctl start firewalld若遇到无法开启 先用&#xff1a;systemctl unmask firewalld.service 然后&a…
阅读更多...
Java继承——抽象类与接口的比较以及内部类、匿名类、异常类......

Java继承——抽象类与接口的比较以及内部类、匿名类、异常类......

文章目录壹、抽象类与接口的比较贰、内部类叁、匿名类&#xff08;匿名内部类&#xff09;肆、异常类&#xff08;Exception&#xff09;壹、抽象类与接口的比较 1、抽象类与接口都可以有抽象方法&#xff1b; 2、接口中只可以有常量&#xff0c;不可以有变量&#xff1b;而抽…
阅读更多...
Mac | 使用 Wineskin 在 Mac 上运行 exe 程序

Mac | 使用 Wineskin 在 Mac 上运行 exe 程序

​1 Wineskin 简介 Wineskin is a user-friendly tool used to make ports of Microsoft Windows software to macOS. 很多实用工具只有 Windows 版本&#xff0c;而 Mac 机器本身不支持运行 exe 程序&#xff0c;除了安装双系统、虚拟机等方法外&#xff0c;Wineskin 可以将…
阅读更多...
使用HTML+CSS实现一个静态页面——面包蛋糕 (9页)

使用HTML+CSS实现一个静态页面——面包蛋糕 (9页)

&#x1f380; 精彩专栏推荐&#x1f447;&#x1f3fb;&#x1f447;&#x1f3fb;&#x1f447;&#x1f3fb; ✍️ 作者简介: 一个热爱把逻辑思维转变为代码的技术博主 &#x1f482; 作者主页: 【主页——&#x1f680;获取更多优质源码】 &#x1f393; web前端期末大作业…
阅读更多...
xlsx库实现纯前端导入导出Excel

xlsx库实现纯前端导入导出Excel

前言 最近做了前端导入、导出 Excel 的需求&#xff0c;用到了js-xlsx这个库&#xff0c;该库文档提供的用例很少&#xff0c;并不是很友好。本文总结一下我是如何实现需求的。 需求 提供一个 Excel 文件&#xff0c;将里面的内容转成 JSON 导入数据提供一个 JSON 文件&…
阅读更多...
3D-2D：PnP

3D-2D：PnP

直接线性变换 Perspective-n-Point 是求解3D到2D点对运动的方法。它描述了已知n个3D空间点及其投影位置时&#xff0c;如何估计相机的位姿。 2D-2D的对极几何方法需要8个或8个以上的点对(以八点法为例)&#xff0c;且存在初始化、纯旋转和尺度的问题。然而&#xff0c;如果两张…
阅读更多...
【数据挖掘】数据预处理

【数据挖掘】数据预处理

Outline ChapterOverview1.为什么要对数据预处理2.数据描述性总结3.数据清洗4.数据变换5.数据整合6.数据归约7.离散化与概念层级8.总结Chapter 1. 为什么要预处理 我们从现实生活中获得的原始数据&#xff0c;或多或少会因为各种原因不能直接使用。例如&#xff1a; 不完整 …
阅读更多...
K8S Pod Sidecar 应用场景之一-加入 NGINX Sidecar 做反代和 web 服务器

K8S Pod Sidecar 应用场景之一-加入 NGINX Sidecar 做反代和 web 服务器

Kubernetes Pod Sidecar 简介 Sidecar 是一个独立的容器&#xff0c;与 Kubernetes pod 中的应用容器一起运行&#xff0c;是一种辅助性的应用。 Sidecar 的常见辅助性功能有这么几种&#xff1a; 服务网格 (service mesh) 代理监控 Exporter&#xff08;如 redis exporter)C…
阅读更多...
【附源码】计算机毕业设计JAVA学校食堂订餐管理

【附源码】计算机毕业设计JAVA学校食堂订餐管理

【附源码】计算机毕业设计JAVA学校食堂订餐管理 目运行 环境项配置&#xff1a; Jdk1.8 Tomcat8.5 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; JAVA my…
阅读更多...
Java#20(包和final)

Java#20(包和final)

目录 一.包 1.包的作用? 2.包名书写的规则? 3.什么是全类名? 4.什么时候需要导包? 什么时候不需要导包? 二.final 三.常量 实际开发中&#xff0c;常量一般作为系统的配置信息&#xff0c;方便维护&#xff0c;提高可读性 四.权限修饰符 五.静态代码块 一.包 1…
阅读更多...
简述使用vue使用webpack脚手架创建项目并升级至webpack4

简述使用vue使用webpack脚手架创建项目并升级至webpack4

第一步、输入命令 vue init webpack demo2 &#xff08;demo2表示项目名称&#xff09;&#xff0c;回车后等待项目完成创建&#xff1b; 第二步、打开package.json&#xff0c;升级以下依赖&#xff08;建议升级一项依赖后运行一下项目&#xff09; webpack系列webpack 3.6.…
阅读更多...
Vue实现下载及文件重命名

Vue实现下载及文件重命名

效果如下&#xff1a; 实现步骤&#xff1a; html&#xff1a; <el-table-column prop"name" label"操作" align"center" header-align"center" width"165"><template slot-scope"scope"><el-but…
阅读更多...
MindSpore和Python中nn.Unfold的区别

MindSpore和Python中nn.Unfold的区别

在往MindSpore迁移项目中遇到了这个转换&#xff0c;以至于不得不去仔细研究一下。 Unfold是卷积操作中的一部分&#xff0c;我们来看一下描述。 Unfold()函数是从一个batch图片中&#xff0c;提取出滑动的局部区域块&#xff0c;也就是卷积操作中的提取kernel filter对应的滑…
阅读更多...
图片如何加水印？教你几招轻松加

图片如何加水印？教你几招轻松加

相信很多喜欢出门游玩的小伙伴&#xff0c;会习惯将旅途中遇到的风景、趣事将其拍照记录下来&#xff0c;然后将图片分享到社交账号上去&#xff0c;但是互联网上什么人都有&#xff0c;总会有不怀好意的人&#xff0c;会在网上拿别人辛苦拍摄的照片&#xff0c;据为己有去发布…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023