直接线性变换

Perspective-n-Point 是求解3D到2D点对运动的方法。它描述了已知n个3D空间点及其投影位置时，如何估计相机的位姿。
2D-2D的对极几何方法需要8个或8个以上的点对(以八点法为例)，且存在初始化、纯旋转和尺度的问题。然而，如果两张图像中的特征点的3D位置已知，那么最少只需3个点对(以及至少一个额外点验证结果)就可以估计相机运动。

已知一组3D点的位置，以及它们在某个相机中的投影位置，求该相机的位姿。这个问题也可以用于求解给定地图和图像时的相机状态问题。如果把3D点看成在另一个相机坐标系的点的话，也可以用来求解两个相机的相对运动问题，如果把3D点看做目标物体自身坐标系中的点的话，也可以用来求解目标物体相对相机的位姿。

考虑某个空间点$P$，它的齐次坐标为$\mathbf{P}=(X,Y,Z,1{)}^T$。在图像$I_1$中，投影到特征点${\mathbf{x}}_1=({\bar{x}}_1,{\bar{y}}_1,1{)}^T$(以归一化平面齐次坐标表示)。此时，相机的位姿$\mathbf{R},\mathbf{t}$是未知的。与单应矩阵的求解类似，我们定义增广矩阵$\begin{array}{ll}[\mathbf{R}& \mathbf{t}]\end{array}$为一个$3\times 4$的矩阵，包含了旋转与平移信息。
$$s\left(\begin{array}{c}{\bar{x}}_1\\ {\bar{y}}_1\\ 1\end{array}\right)=\begin{array}{ll}[\mathbf{R}& \mathbf{t}]\mathbf{P}\end{array}=\left(\begin{array}{cccc}{t}_1& t_2& t_3& t_4\\ t_5& t_6& t_7& t_8\\ t_9& t_{10}& t_{11}& t_{12}\end{array}\right)\left(\begin{array}{c}X\\ Y\\ X\\ 1\end{array}\right)$$
用最后一行把$s$消去，得到两个约束：
$$\begin{gathered} u_1=\frac{t_{1}X+t_{2}Y+t_{3}Z+t_4}{t_{9}X+t_{10}Y+t_{11}Z+t_{12}} \\ {v}_1=\frac{t_{5}X+t_{6}Y+t_{7}Z+t_8}{t_{9}X+t_{10}Y+t_{11}Z+t_{12}} \end{gathered}$$
为简化表示，定义$\mathbf{T}$的行向量：
$$\begin{gathered} {\mathbf{t}}_1={\left(\begin{array}{c}{t}_1,t_2,t_3,t_4\end{array}\right)}^T \\ {\mathbf{t}}_2={\left(\begin{array}{c}{t}_1,t_2,t_3,t_4\end{array}\right)}^T \\ {\mathbf{t}}_1={\left(\begin{array}{c}{t}_1,t_2,t_3,t_4\end{array}\right)}^T \end{gathered}$$
于是有
$$\begin{gathered} {\mathbf{t}}_1^T\mathbf{P}-{\mathbf{t}}_3^T\mathbf{P}{u}_1=0 \\ {\mathbf{t}}_2^T\mathbf{P}-{\mathbf{t}}_3^T\mathbf{P}{v}_1=0 \end{gathered}$$
注意$\mathbf{t}$是待求的变量，每个特征点提供了两个关于$t$的线性约束。假设一共有$N$个特征点，则可以列出如下线性方程组：
$$\left(\begin{array}{ccc}{\mathbf{P}}_1^T& 0& -u_1{\mathbf{P}}_1^T\\ 0& {\mathbf{P}}_1^T& -v_1{\mathbf{P}}_1^T\\ ⋮& ⋮& ⋮\\ {\mathbf{P}}_N^T& 0& -u_N{\mathbf{P}}_N^T\\ 0& {\mathbf{P}}_N^T& -v_N{\mathbf{P}}_N^T\end{array}\right)\left(\begin{array}{c}{\mathbf{t}}_1\\ {\mathbf{t}}_2\\ {\mathbf{t}}_3\end{array}\right)=0$$
$\mathbf{t}$一共有12维，因此最少通过6对匹配点即可实现矩阵T的线性求解，这种方法称为DLT。当匹配点大于6对时，也可以使用SVD等方法对超定方程求最小二乘解。
在DLT求解中我们直接将$\mathbf{T}$矩阵看成了12个未知数，忽略了它们之间的联系。因为旋转矩阵$\mathbf{R}\in \mathrm{S}\mathrm{O}(3)$，用DLT求出的解不一定满足该约束，它是一个一般矩阵。平移向量比较好办，它属于向量空间。对于旋转矩阵$\mathbf{R}$，我们必须针对DLT估计的$\mathbf{T}$左侧$3\times 3$矩阵块，寻找一个最好的旋转矩阵对它进行近似。这可以由QR分解完成，也可以像这样来计算：
$$\mathbf{R}\leftarrow ({\mathbf{R}\mathbf{R}}^T{)}^{-\frac{1}{2}}\mathbf{R}$$

最小化重投影误差求解PnP

前面说的线性方程，往往是先求相机位姿，再求空间点位置，非线性优化则是把它们看成优化变量，放在一起优化。
这是一种非常通用的求解方式，我可以用它对PnP和ICP给出的结果进行优化。这一类把相机和三维点放在一起进行最优化的问题，统称为Bundle Adjustment。

考虑n个三维空间点P及其投影p，我们希望计算相机的位姿$\mathbf{R},\mathbf{t}$，它的李群表示为$\mathbf{T}$ 。假设某空间点坐标为${\mathbf{P}}_i=[X_i,Y_i,Z_i{]}^T$ ，其投影的像素坐标为${\mathbf{q}}_i=[u_i,v_i{]}^T$ 。
$$s_i\left[\begin{array}{c}{u}_i\\ v_i\\ 1\end{array}\right]=\mathbf{K}\mathbf{T}\left[\begin{array}{c}{X}_i\\ Y_i\\ Z_i\\ 1\end{array}\right]$$
写成矩阵形式：
$$s_i{\mathbf{q}}_i={\mathbf{K}\mathbf{T}\mathbf{P}}_i$$
这个式子隐含了一次从齐次坐标到非齐次的转换，由于相机位姿未知及观测点的噪声，该等式存在一个误差。因此，我们把误差求和，构建最小二乘问题，然后寻找最好的相机位姿，使它最小化：
$${\mathbf{T}}^{\ast }=\arg \underset{\mathbf{T}}{\min }\frac{1}{2}\sum _{i=1}^n{\Vert {\mathbf{u}}_i-\frac{1}{s_i}{\mathbf{K}\mathbf{T}\mathbf{P}}_i\Vert }_2^2$$
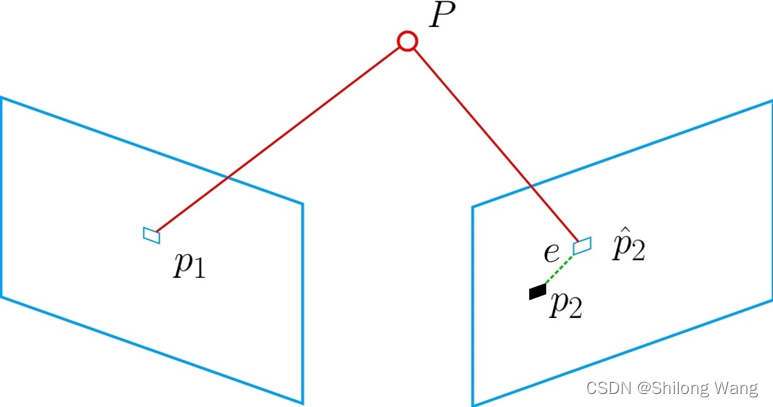
该问题的误差项，是将3D点的投影位置与观测位置作差，所以称为重投影误差。 用齐次坐标时，这个误差有3维。不过，由于$\mathbf{u}$最后一维为1，该维度的误差一直为零， 因而我们更多时使用非齐次坐标，于是误差只有2维了。 我们通过特征匹配知道了$p_1$ 和$p_2$ 是同一个空间点$P$的投影， 但是不知道相机的位姿。在初始值中，$P$的计算投影${\hat{p}}_2$ 与实际的$p_2$之间有一定的距离。于是我们调整相机的位姿，使得这个距离变小 。不过，由于这个调整需要考虑很多个点，所以最后追求的效果是整体误差的缩小，而每个点的误差通常不会精确为零。

我们需要知道每个误差项关于优化变量的导数，也就是线性化
$$e\left(x+\Delta x\right)\approx e\left(x\right)+J^T\Delta x$$
当$e$为像素坐标误差(2维)，$x$维相机位姿(6维)时，$J^T$将是一个$2\times 6$的矩阵。
$$P^{\prime }={\left(TP\right)}_{1:3}={\left[X^{\prime },Y^{\prime },Z^{\prime }\right]}^T$$
那么，相机投影模型相对于$P^{\prime }$为
$$su=K{P}^{\prime }$$
展开：
$$\left[\begin{array}{c}su\\ sv\\ s\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}^{\prime }\\ Y^{\prime }\\ Z^{\prime }\end{array}\right]$$
利用第三行消去$s$(实际上就是$P^{\prime }$的$Z^{\prime }$)，得
$$\begin{gathered} u=f_x\frac{X^{\prime }}{Z^{\prime }}+c_x \\ v=f_y\frac{Y^{\prime }}{Z^{\prime }}+c_y \end{gathered}$$
在定义了中间变量后，我们对$T$左乘扰动量$\delta \xi$，然后考虑$e$的变化关于扰动量的导数。利用链式法则，可以列写如下：
$$\frac{\partial e}{\partial \delta \xi }=\underset{\delta \xi \to 0}{\lim }\frac{e\left(\delta \xi \oplus \xi \right)-e\left(\xi \right)}{\delta \xi }=\frac{\partial e}{\partial P^{\prime }}\frac{\partial P^{\prime }}{\partial \delta \xi }$$
这里的$\oplus$指李代数上的左乘扰动。第一项是误差关于投影点的导数， 已列出了变量之的关 ，易得：
$$\frac{\partial e}{\partial P^{\prime }}=\frac{\partial {\left[u-\bar{u},v-\bar{v}\right]}^T}{\partial P^{\prime }}=\left[\begin{array}{ccc}\frac{\partial u}{\partial X^{\prime }}& \frac{\partial u}{\partial Y^{\prime }}& \frac{\partial u}{\partial Z^{\prime }}\\ \frac{\partial v}{\partial X^{\prime }}& \frac{\partial v}{\partial Y^{\prime }}& \frac{\partial v}{\partial Z^{\prime }}\end{array}\right]=\left[\begin{array}{ccc}\frac{f_x}{Z^{\prime }}& 0& -\frac{f_x{X}^{\prime }}{Z^{\prime 2}}\\ 0& \frac{f_y}{Z^{\prime }}& -\frac{f_y{Y}^{\prime }}{Z^{\prime 2}}\end{array}\right]$$
而第二项为变换后的点关于李代数的导数 ，得：
$$\frac{\partial P^{\prime }}{\partial \delta \xi }=\frac{\partial {\left(TP\right)}_{1:3}}{\partial \delta \xi }={\left(TP\right)}_{1:3}^{\odot }={\left[\begin{array}{cc}I& -P^{\prime \wedge }\\ 0^T& 0^T\end{array}\right]}_{1:3}=\left[\begin{array}{cc}I& -P^{\prime \wedge }\end{array}\right]$$
这两项相乘，得$2\times 6$的雅可比矩阵:
$$\frac{\partial e}{\partial \delta \xi }=\left[\begin{array}{cccccc}\frac{f_x}{Z^{\prime }}& 0& -\frac{f_x{X}^{\prime }}{Z^{\prime 2}}& -\frac{f_x{X}^{\prime }{Y}^{\prime }}{Z^{\prime 2}}& f_x+\frac{f_x{X}^{\prime 2}}{Z^{\prime 2}}& -\frac{f_x{Y}^{\prime }}{Z^{\prime }}\\ 0& \frac{f_y}{Z^{\prime }}& -\frac{f_x{Y}^{\prime }}{Z^{\prime 2}}& -f_y-\frac{f_y{Y}^{\prime 2}}{Z^{\prime 2}}& \frac{f_x{X}^{\prime }{Y}^{\prime }}{Z^{\prime 2}}& \frac{f_y{X}^{\prime }}{Z^{\prime }}\end{array}\right]$$
这个雅可比矩阵描述了重投影误差关于相机位姿李代数的一阶变化关系 。
除了优化位姿
$$\begin{gathered} \frac{\partial e}{\partial P}=\frac{\partial e}{\partial P^{\prime }}\frac{\partial P^{\prime }}{\partial P} \\ \frac{\partial e}{\partial P}=\left[\begin{array}{ccc}\frac{f_x}{Z^{\prime }}& 0& -\frac{f_x{X}^{\prime }}{Z^{\prime 2}}\\ 0& \frac{f_y}{Z^{\prime }}& -\frac{f_y{Y}^{\prime }}{Z^{\prime 2}}\end{array}\right]R \end{gathered}$$

$$P^{\prime }={\left(TP\right)}_{1:3}=RP+t$$

此 ， 果se(3)的 义方式是旋转前，平移 后，只要 这个矩阵的前3列与后3列 调即可。
另一方面，除了优化位 ，我 还希望优化 征 的空 位 。
此，需要讨论e 关于空 P 的导 。所幸这个导 矩阵相 来说 易一些。仍 用 式 则，有：