方式1 错误的动态规划

递归公式为
if (matrix[i][j]‘1’&&matrix[i-1][j-1]‘1’){
int edge=(int) Math.pow(dp[i][j],0.5); // 边长
int addCount = addCount(matrix, i, j, edge);
dp[i][j]=dp[i-1][j-1]+addCount;
max=Math.max(max,dp[i][j]);
}
只根据 dp[i-1][j-1] 与上方,左方的元素来计算最大面积,无法统计 [0,1][1,0] 当前为0,而且左上角也为0

public int maximalSquare(char[][] matrix) {
        //     //1. 定义数组 dp[i][j] grid[i][j] 结尾的陆地上的最大面积
        int[][] dp=new int[matrix.length][matrix[0].length];
        //2.递归公式
        //3.初始化 只要第一行或第一列有一个为1,后面的都为1
        for (int i = 0; i <matrix.length ; i++) {
                if (matrix[i][0]=='1'){
                    dp[i][0] = 1;
                    while (i<matrix.length){
                        dp[i][0] = 1;
                    }
                    break;
                }
        }
        for (int i = 0; i <matrix[0].length ; i++) {
            if (matrix[0][i]=='1'){
                dp[0][i] = 1;
                while (i<matrix.length){
                    dp[0][i] = 1;
                }
                break;
            }
        }
        int max=1;
        // 4. 递归顺序
        for (int i = 1; i < matrix.length; i++) {
            for (int j = 1; j < matrix[0].length; j++) {
                if (matrix[i][j]=='1'&&matrix[i-1][j-1]=='1'){
                    int edge=(int) Math.pow(dp[i][j],0.5); // 边长
                    int addCount = addCount(matrix, i, j, edge);
                    dp[i][j]=dp[i-1][j-1]+addCount;
                    max=Math.max(max,dp[i][j]);
                }else{
                    // 该算法存在缺点  无法统计 [0,1][1,0]  当前为0,而且左上角也为0
                }
            }
        }
        return max;
    }
    public int addCount(char[][] matrix,int i,int j,int edge){
        for (int k = 1; k <=edge ; k++) {
            if (matrix[i-k][j]=='0'||matrix[i][j-k]=='0'){
                return 0;
            }
        }
        return 2*edge+1;
    }   

方式二 动态规划

递归公式:
dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
证明:

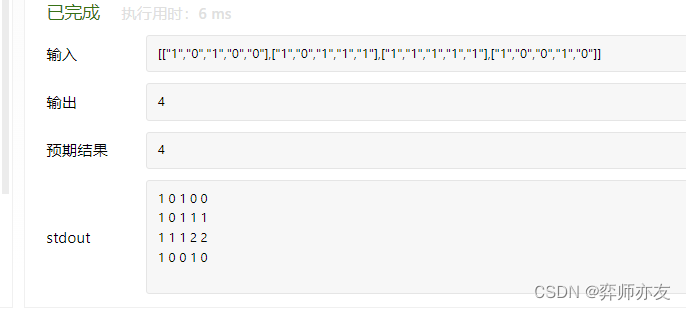
dp[i][j]的含义: 包含matrix[i][j]的最大正方形边长.

  public int maximalSquare(char[][] matrix) {
        //     //1. 定义数组 dp[i][j] grid[i][j] 结尾的陆地上的最大边长
        int[][] dp=new int[matrix.length][matrix[0].length];
        int max=0;
        // 4. 递归顺序
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                if (matrix[i][j] == '1') {
                    if (i==0||j==0){
                        dp[i][j]=1; 
                    }else {
                        dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
                    }
                    max = Math.max(max, dp[i][j]);
                }
            }
        }
        return max*max;
    }