对数尺度的作用

$$y=A{x}^n$$

• 在实验中 $A$ 和 $n$ 都是未知数，现在我想求出 $A$ 和 $n$
• 假设 $n=1.5,A=1$，那么我们可以做个图看看

x = np.linspace(1,10,10)
y = 1 * x**3
plt.plot(y)

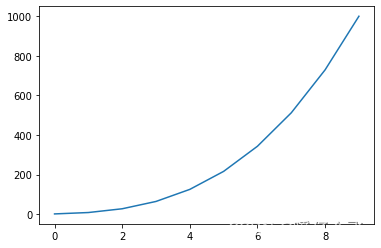
• 如果我做实验恰好得到一些点，那么我很难知道这些点描述的是 $x^3$ 还是 $x^4$ 这其实很难估算

x = np.linspace(1,10,10)
y = 1 * x**3 + np.random.randn(10,) # 随机加一点噪声
plt.scatter(x,y)

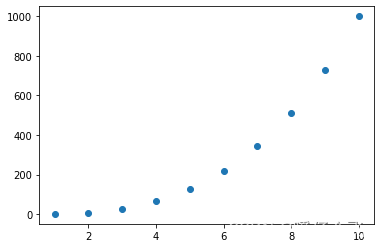
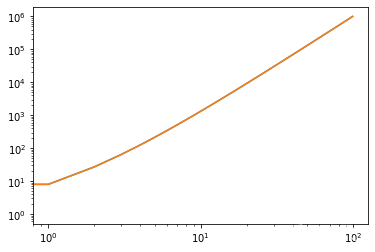
• 但如果我们对这个函数两边取对数，也就是采用对数尺度来衡量这个函数，那么
  $$logy=logA+log{x}^n=logA+nlogx$$

• 即，使用 $log$ 尺度的坐标系的话，这个函数其实可以看做是 $y=A+nx$ 所以在对数标尺的图像应该是个直线

x = np.linspace(1,100,100)
y = 1 * x**3
plt.plot(y)
plt.xscale('log')
plt.yscale('log')
plt.plot(y)