0 导读
如果函数成正交关系,那么它们的积的定积分为 0。反过来说就是,如果两个函数相乘的定积分值为 0,那么称这两个函数正交。sinx 与 cosx 正交,sinnx 与 sinmx 正交(m与n不相等),cosnx 与 cosmx 正交(m与n不相等),sinmx 与 cosmx正交。
1 函数正交定义
如果函数成正交关系,那么它们的积的定积分为 0。反过来说就是,如果两个函数相乘的定积分值为 0,那么称这两个函数正交。
2 正交函数证明
2.1 图形化证明
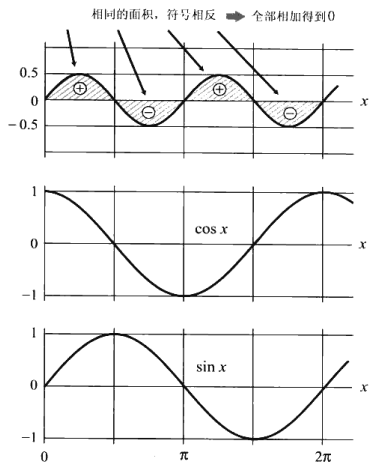
下图最上面为 y = sinx * cosx =1/2 * sinx (积和公式)的图形,中间为 cosx 的图形,最下面是 sinx 的图形
相乘后波峰的定积分是正数,而在波谷,函数的值是负数,面积与波峰相等,但定积分的值是负数。所以,两者相乘定积分的结果为 0 ,故 sinx 与 cosx 函数正交。
2.2 数学计算证明
sinx 与 cosx 定积分

sinx 与 sin2x 定积分
 可以推广到 sinnx 与 sinmx,当 n 与 m 不相等时,sinnx 与 sinmx 正交。
可以推广到 sinnx 与 sinmx,当 n 与 m 不相等时,sinnx 与 sinmx 正交。
同理 cosnx 与 cosmx,当 n 与 m 不相等时,cosnx 与 cosmx 正交。
而且 sinmx 与 cosmx,不论 m 为何值,它们之间总是成正交关系。
3 y=sin2x 与 y=cos2x 的定积分
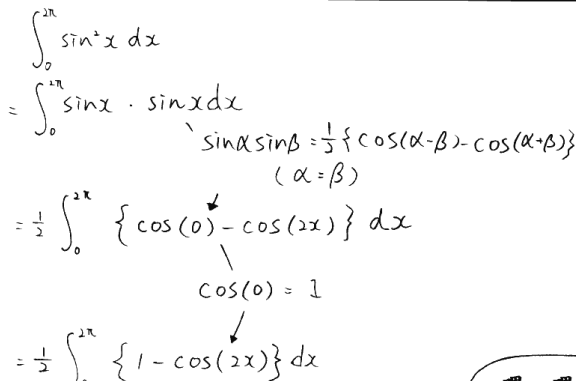
结果为 π。因为 cosx 是 sinx 滞后 π/2 的函数,所以 cos2x 的定积分也是 π











![[CISCN2019 总决赛 Day2 Web1]Easyweb](https://img-blog.csdnimg.cn/b21f1bc85d8043f19509c1a11163f591.png)



