1 PnP问题概述
PnP问题:Perspective-n-Point问题。
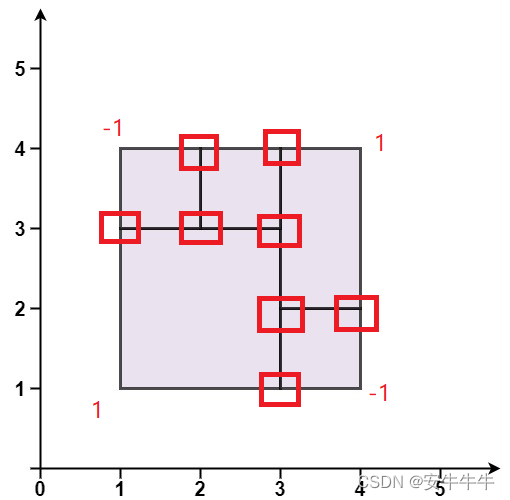
参考下图,

给定n个3D空间参考点,以及各点在相机图像上对应的成像点,求参考点所在坐标系与相机的空间关系。
即:
已知条件1:给定匹配点对:世界坐标系(图中OwXwYwZw)下的n个3D点坐标及其对应在图像坐标系(图中ouv)下的2D点坐标。
已知条件2:相机的内参。
求:世界坐标系OwXwYwZw与相机坐标系OcXcYcZc之间的位姿变换关系。
PnP问题的用途:相机位姿获取,物体位姿测量,AR/VR,机器人操作,SLAM中位姿初值求解……
常用解法:DLT,P3P,EPnP,UPnP。
2 OpenCV的solvePnP
2.1 函数原型定义
OpenCV提供了PnP问题的解算函数,且包含有多种解法。
有以下两个函数。
1) solvePnP
bool solvePnP( InputArray objectPoints, InputArray imagePoints,
InputArray cameraMatrix, InputArray distCoeffs,
OutputArray rvec, OutputArray tvec,
bool useExtrinsicGuess = false, int flags = SOLVEPNP_ITERATIVE );
作用:根据3D-2D点对应关系,获得物体的位姿。
此函数返回旋转和平移向量,可用来将物体坐标系中的3D点变换到相机坐标系下。
2) solvePnPRansac
bool solvePnPRansac( InputArray objectPoints, InputArray imagePoints,
InputArray cameraMatrix, InputArray distCoeffs,
OutputArray rvec, OutputArray tvec,
bool useExtrinsicGuess = false, int iterationsCount = 100,
float reprojectionError = 8.0, double confidence = 0.99,
OutputArray inliers = noArray(), int flags = SOLVEPNP_ITERATIVE );
与solvePnP功能相同,但这个函数使用RANSAC算法剔除异常样本。
RANSAC:Random Sample Consensus(随机抽样一致)。它是根据一组包含异常数据的样本数据集,计算出数据的数学模型参数,得到有效样本数据的算法。它于1981年由Fischler和Bolles最先提出。
因此RANSAC使得PnP函数能够抵抗异常值。
2.2 函数参数
参数:
objectPoints:世界坐标系(上图中OwXwYwZw)下的3D点坐标数组
imagePoints:图像(上图中ouv)中对应3D点的成像点坐标数组
cameraMatrix:相机内参矩阵,3×3
distCoeffs:相机畸变系数数组,可以为NULL,此时视为无畸变。
rvec和tvec:计算结果输出,rvec为旋转向量,tvec为平移向量,两者合并表达的是物体整体(即世界坐标系)在相机坐标系中的位姿
以下参数为可选:
useExtrinsicGuess,这个参数仅用于SOLVEPNP_ITERATIVE,如果为true (1),需要rvec和tvec有输入值,以便函数把输入值作为旋转和平移的估计初始值.
flags:PnP解算方法,详见下节。
solvePnPRansac需要的可选参数
iterationsCount:迭代次数;
reprojectionError:RANSAC使用的内点阈值,即考虑作为内点的观察点与计算点投影之间的最大允许距离
confidence:算法得到有用结果的概率;
inliers:包含 objectPoints 和 imagePoints 中的内点索引的输出向量 .
2.3 PnP解算方法(flags取值)
- SOLVEPNP_ITERATIVE:缺省方法,基于 Levenberg-Marquardt 优化的迭代方法,使重投影误差最小化
- SOLVEPNP_P3P:方法基于论文 X.S. Gao, X.-R. Hou, J. Tang, H.-F. Chang “Complete Solution Classification for the Perspective-Three-Point Problem”
- SOLVEPNP_AP3P:方法基于论文 T. Ke, S. Roumeliotis "An Efficient Algebraic Solution to the Perspective-Three-Point Problem
- SOLVEPNP_EPNP:方法基于论文 F. Moreno-Noguer, V. Lepetit and P. Fua “EPnP: Efficient Perspective-n-Point Camera Pose Estimation”
- SOLVEPNP_DLS:方法基于论文 J. Hesch and S. Roumeliotis. “A Direct Least-Squares (DLS) Method for PnP”
- SOLVEPNP_UPNP:方法基于论文 A. Penate-Sanchez, J. Andrade-Cetto, F. Moreno-Noguer. “Exhaustive Linearization for Robust Camera Pose and Focal Length Estimation”
- SOLVEPNP_IPPE:方法基于论文 T. Collins and A. Bartoli. “Infinitesimal Plane-Based Pose Estimation”
- SOLVEPNP_IPPE_SQUARE:方法基于论文 Toby Collins and Adrien Bartoli. “Infinitesimal Plane-Based Pose Estimation”
- SOLVEPNP_SQPNP:方法基于论文 “A Consistently Fast and Globally Optimal Solution to the Perspective-n-Point Problem” by G. Terzakis and M.Lourakis
2.4 solvePnp的点对
一般来说,解算PnP,最少需要4个物体点与其成像点构成的点对。
当SOLVEPNP_ITERATIVE并且useExtrinsicGuess=true时(rvec和tvec有初值),所需的点数最小可以为3;
P3P methods (SOLVEPNP_P3P, SOLVEPNP_AP3P): 需且仅需4个输入点来获得唯一解;
SOLVEPNP_IPPE:输入点数必须 >= 4,并且所有物体点必须共面;
SOLVEPNP_IPPE_SQUARE:对点的顺序有规定,具体这里略;
除了这几个外,其它方法(flags)要求点的数量必须 >= 4 ,对物体点位置顺序等没有特殊规定。
3 solvePnP使用
使用solvePnP前,需要已具备如下参数:
vector<Point3f>objPts; //3D点数组,世界坐标系物体点坐标,至少4个点
vector<Point2f>imgPts; //2D点数组,与以上物体点一一对应的图像点坐标
Mat cameraMatrix; //相机内参矩阵,3x3矩阵
然后调用
Mat rvec, tvec; //声明用于接收运算结果的两个矢量
solvePnP(objPts, imgPts, cameraMatrix, NULL, rvec, tvec);
得到解算结果后,rvec为旋转矢量形式,后续计算不方便,所以一般会用Rodrigues转为旋转矩阵,以下直接将rvec和tvec一起转为位姿矩阵
Mat wldInCam = Mat::zeros(4, 4, CV_64FC1);
Rodrigues(rvec, wldInCam(Rect(0, 0, 3, 3)));
tvec.copyTo(wldInCam(Rect(0, 3, 1, 3)));
以上得到的wldInCam即为世界坐标系在相机坐标系中的位姿,如果需要求相机在世界坐标系中的位姿,可取逆即可:
Mat camInWld = wldInCam.inv();
参考
[PnP] PnP问题之DLT解法