0 前言
本文以一个小小的案例展开,主要讲解了线性回归的步骤、常用的两种求最优解的方法(最小二乘法和sklearn回归算法及算法原理)及相关函数、公式的过程推导。
相关环境:
Windows 64位
Python3.9
scikit-learn==1.0.2
pandas==1.4.2
numpy==1.21.5
matplotlib==3.5.1
1 案例数据及数据关系
假设有一组数如下,问(10,27)是否合理?
| x | y |
|---|---|
| 1 | 5 |
| 2 | 6 |
| 3 | 9 |
| 4 | 11 |
| 5 | 13 |
要回答这个问题,可以分三步走:
1、确认x和y的关系;
2、拟合模型,并根据模型进行预测;
3、判断(10,27)是否合理。
要确定关系,可以将数据通过散点图绘制出来
import pandas as pd
import matplotlib.pyplot as plt
df = pd.DataFrame({'x':list(range(1,6)),'y':[5,6,9,11,13]})
plt.scatter(df.x,df.y)
plt.show()
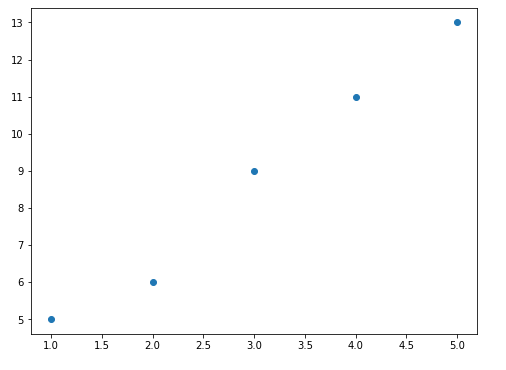
由散点图可见,这是一个线性回归模型,故令线性模型函数为
f
(
x
i
)
=
a
x
i
+
b
f \left( {x}_i \right)=ax_i+b
f(xi)=axi+b,使得
f
(
x
i
)
≈
y
i
f \left( x_i \right) \approx y_i
f(xi)≈yi。
这时,一开始的问题就转化成了求系数a和截距b。
2 拟合模型,求最优解
什么时候a和b达到最优解,也就是拟合效果最好呢?
如果根据过往数学经验,就是画一条直线,尽可能多的过一些散点或靠近散点更多的地方,但是这条线是不是最优的,还不确定,需要通过计算每一条线的拟合结果来确定。判断拟合结果好坏,有一个常用的判断方法:最小二乘法(LS) 得到的值尽可能小。
最小二乘法用通俗的话讲,就是将每个点的实际值
y
i
y_i
yi和直线的预测值
f
(
x
i
)
f \left( x_i \right)
f(xi)相减,然后平方,然后求和。
特殊情况下,当该结果值为0时,说明实际的点和直线的点完全重合,其实就是直线上取出来的点。
最小二乘法的公式如下:
L
S
=
∑
i
=
1
m
(
f
(
x
i
)
−
y
i
)
2
,
其
中
f
(
x
i
)
=
a
x
i
+
b
(2.1)
LS=\sum_{i=1}^m{ \left( f \left( x_i \right) - y_i \right) ^2 },其中f \left( {x}_i \right)=ax_i+b \text{(2.1)}
LS=∑i=1m(f(xi)−yi)2,其中f(xi)=axi+b(2.1)
均分误差(MSE,也称平方损失)的公式如下:
M
S
E
=
1
m
∑
i
=
1
m
(
f
(
x
i
)
−
y
i
)
2
,
其
中
f
(
x
i
)
=
a
x
i
+
b
(2.2)
MSE=\dfrac{1}{m}\sum_{i=1}^m{ \left( f \left( x_i \right) - y_i \right) ^2 },其中f \left( {x}_i \right)=ax_i+b \text{(2.2)}
MSE=m1∑i=1m(f(xi)−yi)2,其中f(xi)=axi+b(2.2)
注:m 表示点的总数,i 表示每个点。
二者差别在于最小二乘法没有除以m,均方差除以m。在某些场景会有变形,比如加权最小二乘法和加权均方差,权重是对应值出现的概率。
在周志华的机器学习一书讲到的一个概念是“最小二乘法是基于均方误差最小化来进行模型求解的方法”,即:
m
i
n
i
m
i
z
e
M
S
E
⇒
模
型
L
S
\boxed{ minimize MSE \xRightarrow{模型} LS}
minimizeMSE模型LS
介绍完LS和MSE,再回到一开始的问题,什么时候a和b达到最优解,可以通过求导方式求解,即在均方差函数上分别对相关未知变量求导,再令导函数
f
′
=
0
f' =0
f′=0进行求解;也可以通过算法进行定向的搜索求解,即先分别给a和b先赋一个初始值,然后通过梯度下降算法,不断更新a和b的值,最终收敛到极值,得到最优解。
2.1 均方差求导求解
如何在均方差
E
(
a
,
b
)
=
1
m
∑
i
=
1
m
(
f
(
x
i
)
−
y
i
)
2
E\left( a,b \right)=\dfrac{1}{m} \textstyle \sum_{i=1}^m{ \left( f \left( x_i \right) - y_i \right) ^2 }
E(a,b)=m1∑i=1m(f(xi)−yi)2上,分别对a和b求导呢?
先把
f
(
x
i
)
=
a
x
i
+
b
f \left( {x}_i \right)=ax_i+b
f(xi)=axi+b代入上式,得到
E
(
a
,
b
)
=
1
m
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
2
(
2.3
)
=
1
m
∑
i
=
1
m
(
x
i
2
a
2
+
2
(
b
−
y
i
)
x
i
a
+
(
b
−
y
i
)
2
)
(
2.4
)
=
1
m
∑
i
=
1
m
(
b
2
+
2
(
a
x
i
−
y
i
)
b
+
(
a
x
i
−
y
i
)
2
)
(
2.5
)
\begin{aligned} E\left( a,b \right) &= \dfrac{1}{m} \displaystyle \sum_{i=1}^m{ \left( ax_i+b - y_i \right) ^2 } &{(2.3)} \\ &= \dfrac{1}{m} \displaystyle \sum_{i=1}^m{\left( x_i^2a^2 + 2 \left(b-y_i \right)x_ia + \left(b-y_i \right)^2 \right)} &{(2.4)} \\ &= \dfrac{1}{m} \displaystyle \sum_{i=1}^m{\left( b^2 + 2 \left(ax_i-y_i \right)b + \left(ax_i-y_i \right)^2 \right)} &{(2.5)} \end{aligned}
E(a,b)=m1i=1∑m(axi+b−yi)2=m1i=1∑m(xi2a2+2(b−yi)xia+(b−yi)2)=m1i=1∑m(b2+2(axi−yi)b+(axi−yi)2)(2.3)(2.4)(2.5)
当对a求导时,可以改为(2.4)式的结构以便查看;当对b求导时,可以改为(2.5)式的结构以便查看。求导结果为:
∂ ∂ a E ( a , b ) = 2 m ∑ i = 1 m ( a x i + b − y i ) x i ( 2.6 ) ∂ ∂ b E ( a , b ) = 2 m ∑ i = 1 m ( a x i + b − y i ) ( 2.7 ) \begin{aligned} \dfrac{\partial}{\partial a} E_{(a,b)} &=\dfrac{2}{m} \displaystyle \sum_{i=1}^m{ \left( ax_i+b-y_i \right)x_i } &{(2.6)} \\ \dfrac{\partial}{\partial b} E_{(a,b)} &=\dfrac{2}{m} \displaystyle \sum_{i=1}^m{\left( ax_i+b-y_i \right)} &{(2.7)} \end{aligned} ∂a∂E(a,b)∂b∂E(a,b)=m2i=1∑m(axi+b−yi)xi=m2i=1∑m(axi+b−yi)(2.6)(2.7)
令(2.6)式和(2.7)式都为0,并结合新得到的两个等式,可得到解:
a
=
∑
i
=
i
m
(
y
1
−
y
‾
)
x
i
∑
i
=
i
m
(
x
1
−
x
‾
)
x
i
或
∑
i
=
1
m
(
x
i
−
x
‾
)
y
i
∑
i
=
i
m
(
x
1
−
x
‾
)
x
i
或
∑
i
=
i
m
(
y
1
−
y
‾
)
(
x
i
−
x
‾
)
∑
i
=
i
m
(
x
1
−
x
‾
)
2
或
=
∑
i
=
i
m
x
i
y
1
−
m
x
‾
y
‾
∑
i
=
i
m
x
i
2
−
m
x
‾
2
(2.9)
a=\dfrac{ \displaystyle \sum_{i=i}^m{\left( y_1 - \overline{y} \right) x_i}}{\displaystyle \sum_{i=i}^m{\left( x_1 - \overline{x} \right) x_i}} 或 \dfrac{ \displaystyle \sum_{i=1}^m{\left( x_i-\overline{x} \right)y_i} }{\displaystyle \sum_{i=i}^m{\left( x_1 - \overline{x} \right) x_i}} 或 \dfrac{ \displaystyle \sum_{i=i}^m{\left( y_1 - \overline{y} \right) \left( x_i -\overline{x} \right)}}{\displaystyle \sum_{i=i}^m{\left( x_1 - \overline{x} \right)^2}} 或=\dfrac{ \displaystyle \sum_{i=i}^m{ x_iy_1 } -m\overline{x}\overline{y} }{ \displaystyle \sum_{i=i}^m{ x_i^2 } -m\overline{x}^2 } \text{(2.9)}
a=i=i∑m(x1−x)xii=i∑m(y1−y)xi或i=i∑m(x1−x)xii=1∑m(xi−x)yi或i=i∑m(x1−x)2i=i∑m(y1−y)(xi−x)或=i=i∑mxi2−mx2i=i∑mxiy1−mxy(2.9)
b
=
1
m
∑
i
=
1
m
(
y
i
−
a
x
i
)
=
y
‾
−
a
x
‾
(2.10)
b=\dfrac{1}{m} \displaystyle \sum_{i=1}^m{\left( y_i-ax_i \right)}=\overline{y}-a\overline{x} \text{(2.10)}
b=m1i=1∑m(yi−axi)=y−ax(2.10)
注:a的4个分子得到一样的值,3个分母也是,可以有多种组合。以上公式具体推导过程可以看公式推导小节。
该组数据得到的解为a=2.1;b=2.5。
import pandas as pd
import matplotlib.pyplot as plt
df = pd.DataFrame({'x':list(range(1,6)),'y':[5,6,9,11,13]})
plt.figure(figsize=(8,6))
plt.scatter(df.x,df.y)
plt.plot(df.x,df.x*2.1+2.5)
plt.show()
print(2.1*10+2.5) # 结果为23.5
拟合结果如下: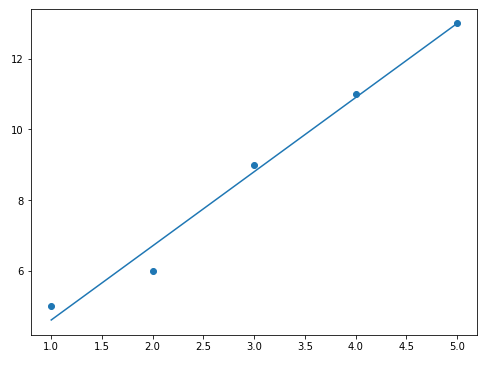
插播:导数的作用
导数的作用:导数描述了一个函数在某一点上的变化率,这个变化率的大小需要根据导数结果定义。
比如直线函数(如
y
=
x
y=x
y=x,其求导函数为
y
′
=
1
y'=1
y′=1)的导数是一个自然数(
数
字
1
数字1
数字1),那么整一条直线上的任意一个点的导数都是该值,变化率不变。
如果是曲线函数(如
y
=
x
2
y=x^2
y=x2,其求导函数为
y
′
=
2
x
y'=2x
y′=2x),其导数会根据点在不同的位置上得到一个变化率(
y
′
y'
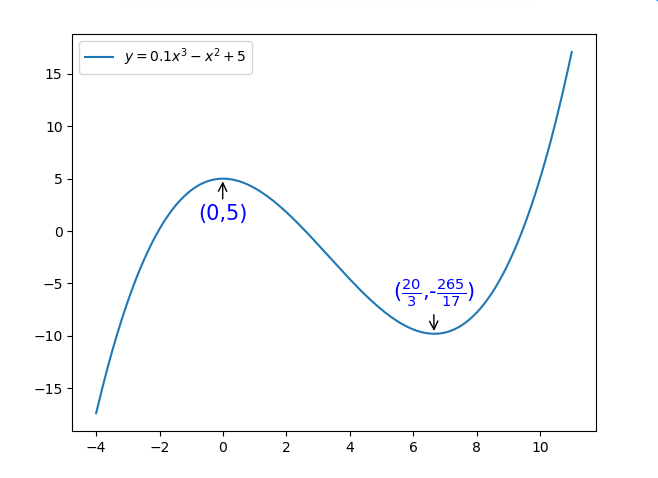
y′),也表示为该点上的切线斜率,切线斜率越小,表示越接近全局或局部的最值(最大或最小值),当切线斜率为0时,达到最值(可能是全局也可能是局部,结合函数判断,最高幂次方为2次则只有一个最值),如下图1。
导数的作用就是帮助我们通过切线斜率等于0时找到最值,一般该值就是原函数的最优解。当然了,如果一个函数有多个切线斜率等于0,可能会取到局部的最优解,而不是全局最优解。(如下图2)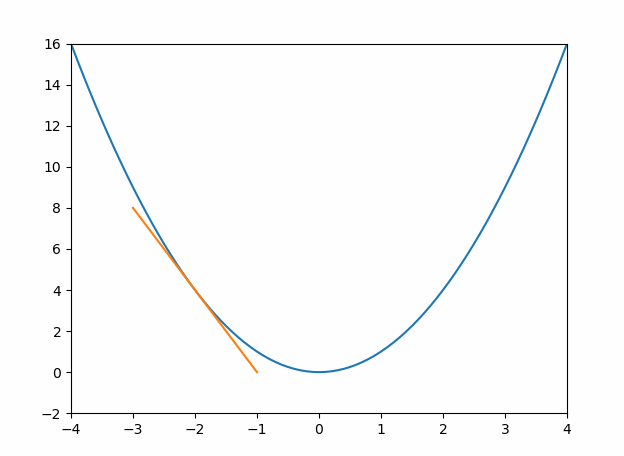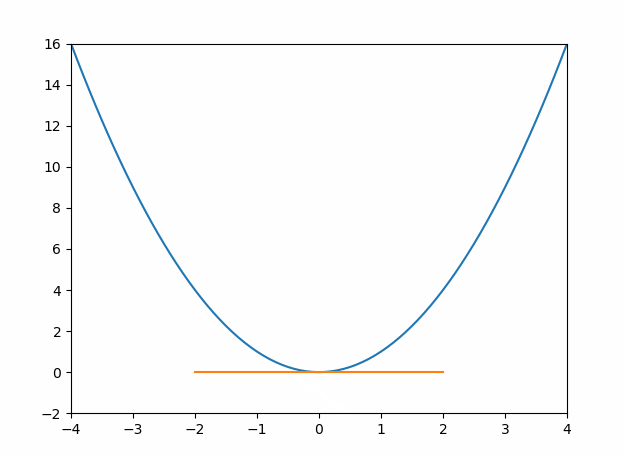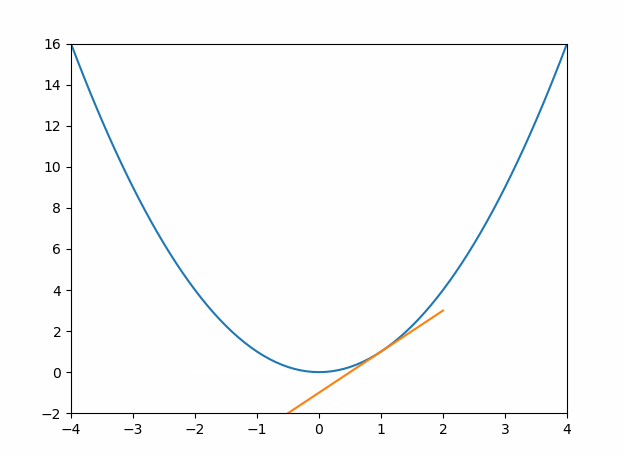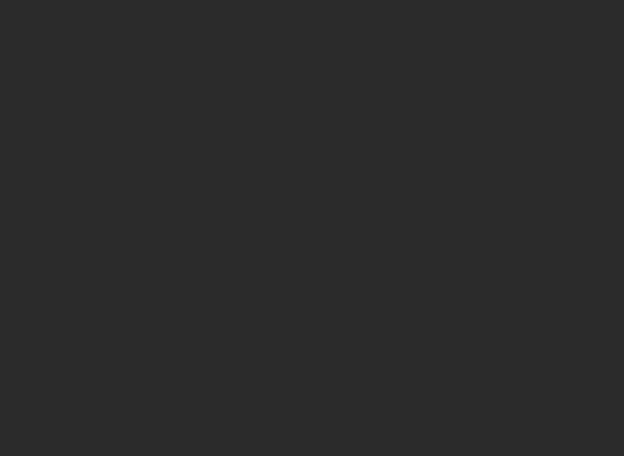
2.2 算法拟合求解
接下来看看算法实现的方式,算法实现的过程是通过定向的搜索。
先来看一个图,如下图,这也是一种搜索的过程,直接在原散点上找拟合效果比较好的线。不过该方法难以判断什么时候能够达到最优解。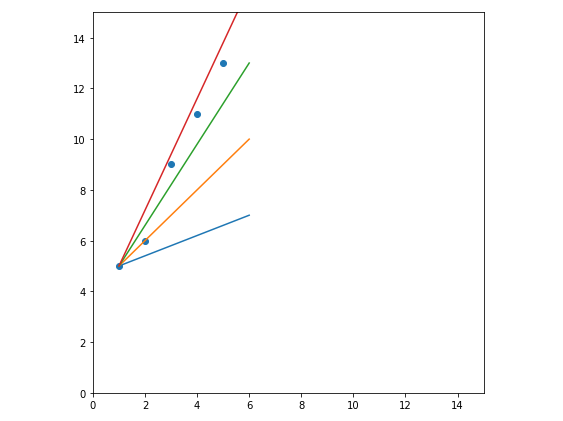
这时候需要更加科学的方式来解决以上问题,前辈们已经为我们创造了好多算法用于搜索最优解。这些算法中有一个表经典的就是梯度下降法。该算法和前面的导函数有些相同之处,在寻找极值的时候,通过对函数对应的梯度不断进行迭代和搜索,最终在极值点收敛。如下图: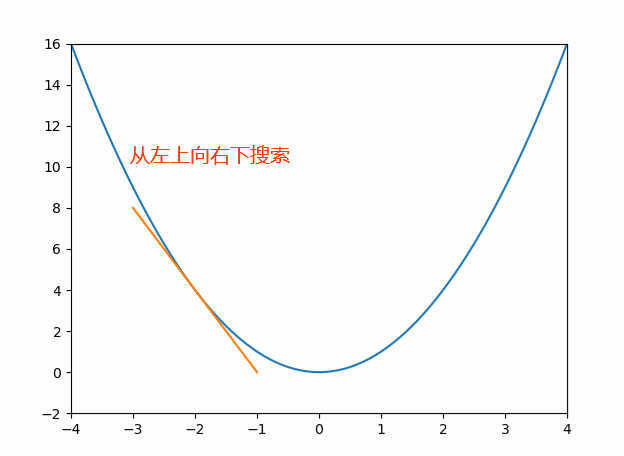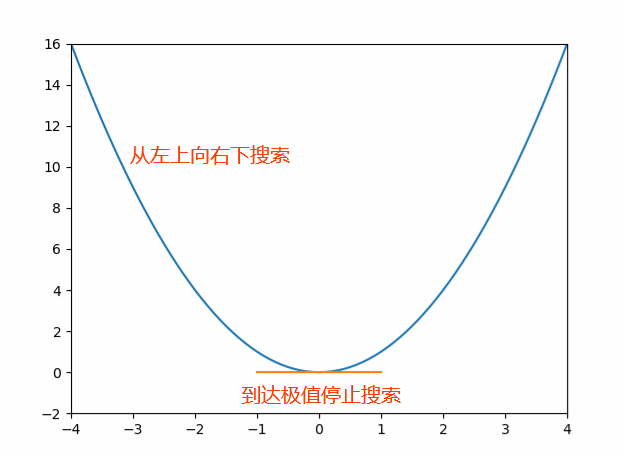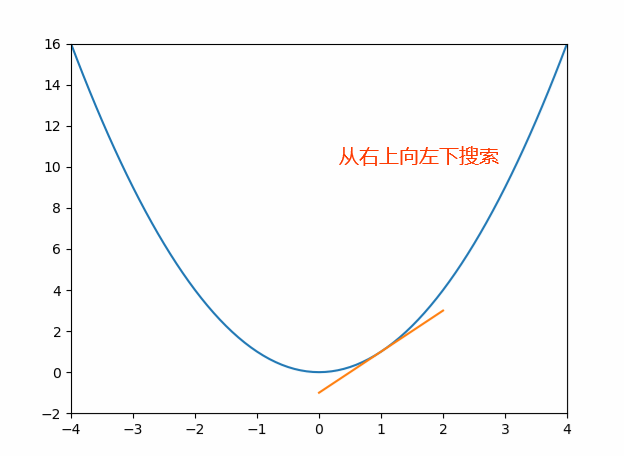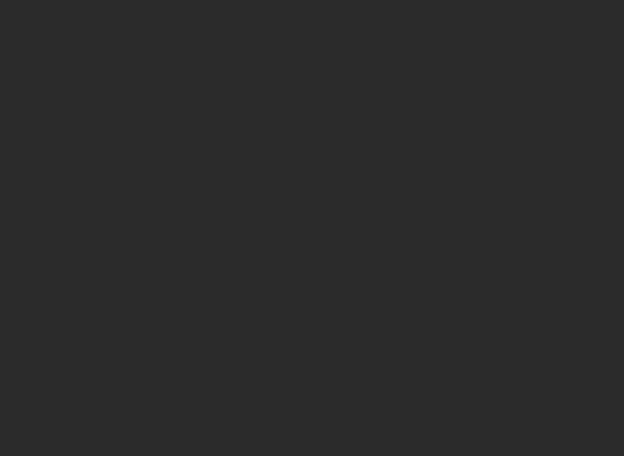
这是二维的展示,如果是三维的,可以参考吴恩达机器学习课程的一张经典的图:
注:
J
(
θ
0
,
θ
1
)
J \left( \theta_0,\theta_1 \right)
J(θ0,θ1)是代价函数,同本文的
J
(
a
,
b
)
J \left( a,b \right)
J(a,b),
θ
0
\theta_0
θ0和
θ
1
\theta_1
θ1则类比a和b,是代价函数(下面讲)的最优解。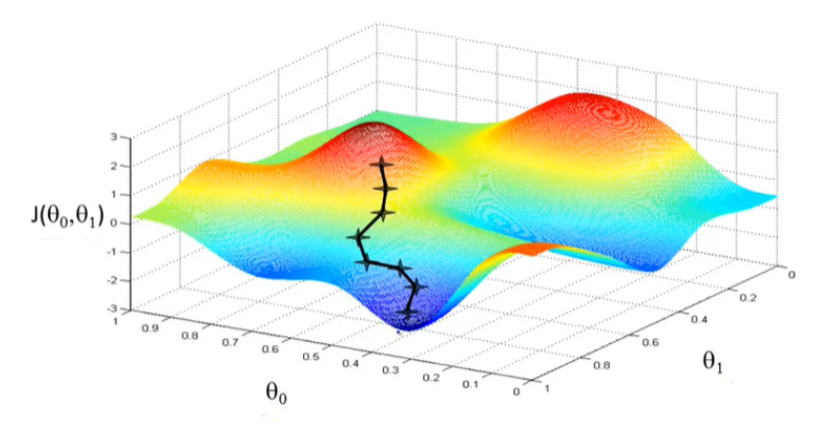
梯度下降的算法逻辑很简单,不过用公式和求解表示会有一点复杂。
讲该算法之前,先引入另外一个概念:损失函数(也叫代价函数)。随着算法不断的发展,损失函数也不断发展。本文建一个比较经典的,就是基于均方差演变而来的,即在均方差的计算结果除以2,看了好些资料,介绍这个2,主要是用于约掉均方差求导后的系数2,以便于计算,姑且这么理解吧。
本次引入的损失函数如下:
J
(
a
,
b
)
=
1
2
m
∑
i
=
1
m
(
f
(
x
i
)
−
y
i
)
2
(2.11)
J\left( a,b \right)=\dfrac{1}{2m}\sum_{i=1}^m{ \left( f \left( x_i \right) - y_i \right) ^2 } \text{(2.11)}
J(a,b)=2m1∑i=1m(f(xi)−yi)2(2.11)
注:损失函数和代价函数的差别在于损失函数定义在单个样本,是一个样本的误差,代价函数定义在整个训练集,是所有样本的平均误差。
梯度下降算法的公式如下:
a
i
+
1
=
a
i
−
α
∂
∂
a
i
J
(
a
,
b
)
(
2.12
)
b
i
+
1
=
b
i
−
α
∂
∂
b
i
J
(
a
,
b
)
(
2.13
)
\begin{aligned} a_{i+1} &= a_i - \alpha \dfrac{\partial}{\partial a_i} J_{(a,b)} &{(2.12)} \\ b_{i+1} &= b_i - \alpha \dfrac{\partial}{\partial b_i} J_{(a,b)} &{(2.13)} \end{aligned}
ai+1bi+1=ai−α∂ai∂J(a,b)=bi−α∂bi∂J(a,b)(2.12)(2.13)
这两个公式是迭代公式,就是下一次的a和b值由本次得到的a和b值减去后面一长串公式得到的结果。
α
\alpha
α是学习速率,或者叫步长,就是你给算法定义的值,每次期望移动多大值;
∂
∂
a
J
(
a
,
b
)
\dfrac{\partial}{\partial a} J_{(a,b)}
∂a∂J(a,b)和
∂
∂
b
J
(
a
,
b
)
\dfrac{\partial}{\partial b} J_{(a,b)}
∂b∂J(a,b)是求导公式,即在损失函数上,对a和b分别求导。
补充说明:可能有的小伙伴对于对a和b分别求导有点无厘头,特别是多个位置参数放在一起的时候,更容易混淆。无论如何复杂,认准一点,对谁求导,谁就是自变量,其他的全部视为常数,然后根据求导的规则获取导函数。比如:
f
(
x
)
=
a
x
2
+
b
x
+
c
f \left( x \right)=ax^2+bx+c
f(x)=ax2+bx+c对a求导就是
f
′
(
a
)
=
x
2
f' \left( a \right)=x^2
f′(a)=x2,对b求导就是
f
′
(
b
)
=
x
f' \left( b \right)=x
f′(b)=x,对c求导就是
f
′
(
c
)
=
1
f' \left( c \right)=1
f′(c)=1。
如何在代价函数
J
(
a
,
b
)
=
1
2
m
∑
i
=
1
m
(
f
(
x
i
)
−
y
i
)
2
J\left( a,b \right)=\dfrac{1}{2m} \textstyle \sum_{i=1}^m{ \left( f \left( x_i \right) - y_i \right) ^2 }
J(a,b)=2m1∑i=1m(f(xi)−yi)2上,分别对a和b求导呢?这个和上文讲均方差求导时有介绍过类似内容,只不过前面是均方差,此处是代价函数,多除以2,其他基本一致。
先把
f
(
x
i
)
=
a
x
i
+
b
f \left( {x}_i \right)=ax_i+b
f(xi)=axi+b代入上式,得到
J
(
a
,
b
)
=
1
2
m
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
2
(
2.14
)
=
1
2
m
∑
i
=
1
m
(
x
i
2
a
2
+
2
(
b
−
y
i
)
x
i
a
+
(
b
−
y
i
)
2
)
(
2.15
)
=
1
2
m
∑
i
=
1
m
(
b
2
+
2
(
a
x
i
−
y
i
)
b
+
(
a
x
i
−
y
i
)
2
)
(
2.16
)
\begin{aligned} J\left( a,b \right) &= \dfrac{1}{2m} \displaystyle \sum_{i=1}^m{ \left( ax_i+b - y_i \right) ^2 } &{(2.14)} \\ &= \dfrac{1}{2m} \displaystyle \sum_{i=1}^m{\left( x_i^2a^2 + 2 \left(b-y_i \right)x_ia + \left(b-y_i \right)^2 \right)} &{(2.15)} \\ &= \dfrac{1}{2m} \displaystyle \sum_{i=1}^m{\left( b^2 + 2 \left(ax_i-y_i \right)b + \left(ax_i-y_i \right)^2 \right)} &{(2.16)} \end{aligned}
J(a,b)=2m1i=1∑m(axi+b−yi)2=2m1i=1∑m(xi2a2+2(b−yi)xia+(b−yi)2)=2m1i=1∑m(b2+2(axi−yi)b+(axi−yi)2)(2.14)(2.15)(2.16)
当对a求导时,可以改为(2.15)式的结构以便查看;当对b求导时,可以改为(2.16)式的结构以便查看。求导结果为:
∂
∂
a
J
(
a
,
b
)
=
1
m
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
x
i
(
2.17
)
∂
∂
b
J
(
a
,
b
)
=
1
m
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
(
2.18
)
\begin{aligned} \dfrac{\partial}{\partial a} J_{(a,b)} &=\dfrac{1}{m} \displaystyle \sum_{i=1}^m{ \left( ax_i+b-y_i \right)x_i } &{(2.17)} \\ \dfrac{\partial}{\partial b} J_{(a,b)} &=\dfrac{1}{m} \displaystyle \sum_{i=1}^m{\left( ax_i+b-y_i \right)} &{(2.18)} \end{aligned}
∂a∂J(a,b)∂b∂J(a,b)=m1i=1∑m(axi+b−yi)xi=m1i=1∑m(axi+b−yi)(2.17)(2.18)
注:具体推导过程可以看公式推导小节。
将(2.17)代入(2.12),将(2.18)代入(2.13),便可以得到:
a
i
+
1
=
a
i
−
α
1
m
∑
i
=
1
m
(
a
i
x
i
+
b
i
−
y
i
)
x
i
(
2.19
)
b
i
+
1
=
b
i
−
α
1
m
∑
i
=
1
m
(
a
i
x
i
+
b
i
−
y
i
)
(
2.20
)
\begin{aligned} a_{i+1} &= a_i - \alpha \dfrac{1}{m} \displaystyle \sum_{i=1}^m{ \left( a_ix_i+b_i-y_i \right)x_i } &{(2.19)} \\ b_{i+1} &= b_i - \alpha \dfrac{1}{m} \displaystyle \sum_{i=1}^m{ \left( a_ix_i+b_i-y_i \right) } &{(2.20)} \end{aligned}
ai+1bi+1=ai−αm1i=1∑m(aixi+bi−yi)xi=bi−αm1i=1∑m(aixi+bi−yi)(2.19)(2.20)
注:右边的a和b的结构都是本次的a和b,左边的a和b是下一次值,二者同步更新。用Python实现过程,或需要新建一个中间变量,以避免在计算完(2.19)式之后,变量a 变成了下一次的值,等到计算(2.20)式时,使用下一次的a 值更新下一次的b 值。
如果通过Python实现们可以直接调用scikit-learn(sklearn)的线性回归模型库实现,具体代码实现步骤如下:
# 读取数据
import pandas as pd
data = pd.DataFrame({'x':[1,2,3,4,5],'y':[5,6,9,11,13]})
# data.shape,type(data)
x = data.loc[:,'x']
y = data.loc[:,'y']
# 画图查看数据分布
from matplotlib import pyplot as plt
plt.figure(figsize=(8,6))
plt.scatter(x,y)
plt.show()
# 调用sklearn的线性模型
from sklearn.linear_model import LinearRegression
lr_model = LinearRegression()
# 转换维度,一维转为二维
X = x.values.reshape(-1, 1)
# 训练模型
lr_model.fit(X,y)
# 预测x结果
y_predict = lr_model.predict(X)
# 画图查看y和y_predict
plt.figure(figsize=(8,6))
plt.scatter(x,y)
plt.plot(x,y_predict)
plt.show()
# 打印a、b值
a = lr_model.coef_
b = lr_model.intercept_
print(a,b) # 结果为:[2.1] 2.499999999999999
# 查看均方差
from sklearn.metrics import mean_squared_error,r2_score
MSE = mean_squared_error(y,y_predict)
R2 = r2_score(y,y_predict)
print(MSE,R2) # 结果为:0.13999999999999996 0.984375
# 预测具体某个值的结果
y_p = lr_model.predict([[10]])
print(y_p) # 结果为:[23.5]
拟合的曲线为:
f
(
x
i
)
=
2.1
x
i
+
2.5
f \left( {x}_i \right)=2.1x_i+2.5
f(xi)=2.1xi+2.5
拟合结果可视化如下: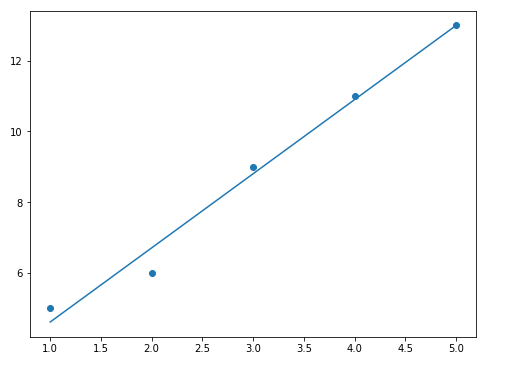
3 判断结果
通过以上两种求解方法得到的结果均为23.5。(10,27)点在拟合直线的上方,27比23.5大3.5。
是否合理呢?可以通过
R
2
R^2
R2来衡量,在算法计算中有计算过该值,为0.984375,也就是说,在该模型的拟合效果上,有98.4%的可信度相信当x=10时,得到23.5。所以27是不合理的。但是,需要注意的是,该可信度是基于已知的5个点训练得到的结果,由于数量较少,对x>5之外的值可能不适用,当然,如果是相同的场景下,或有一定的适用性,权当教学使用。
虽然27不合理,但是在涉及到决策时,需要再结合实际的情况做出是否接受的判断,比如说如果是某地的房价预测是23.5万/平,实际出价是27万/平,对于卖方有利,对于卖方无利。站在卖方角度,一般可接受,站在买方角度,一般不可接受。
4 公式推导
4.1 如何证明 ∑ i = 1 m ( x i − x ‾ ) x i = ∑ i = 1 m ( x i − x ‾ ) 2 = ∑ i = i m x i 2 − m x ‾ 2 \textstyle\sum_{i=1}^m{ \left( {x}_i-\overline{x} \right)x_i} =\textstyle\sum_{i=1}^m{ \left( {x}_i-\overline{x} \right)^2} =\textstyle \sum_{i=i}^m{ x_i^2 } -m\overline{x}^2 ∑i=1m(xi−x)xi=∑i=1m(xi−x)2=∑i=imxi2−mx2成立?
∑
i
=
1
m
x
i
=
x
1
+
x
2
+
x
3
+
⋅
⋅
⋅
⋅
⋅
⋅
+
x
m
=
m
x
‾
=
∑
i
=
1
m
x
‾
(4.1)
\displaystyle\sum_{i=1}^m{ {x}_i} = x_1+x_2+x_3+··· ···+x_m=m \overline{x} =\displaystyle\sum_{i=1}^m{\overline{x}} \text{(4.1)}
i=1∑mxi=x1+x2+x3+⋅⋅⋅⋅⋅⋅+xm=mx=i=1∑mx(4.1)
(4.1)式,x的m个样本值加起来等于m倍均值,可表示为
∑
i
=
1
m
x
‾
\textstyle \sum_{i=1}^m{\overline{x}}
∑i=1mx,即m个
x
‾
\overline{x}
x相加。
∑
i
=
1
m
(
x
‾
x
i
)
=
x
‾
∑
i
=
1
m
x
i
(4.2)
\displaystyle\sum_{i=1}^m{ \left( \overline{x} x_i \right)}=\overline{x}\displaystyle\sum_{i=1}^m{x_i} \text{(4.2)}
i=1∑m(xxi)=xi=1∑mxi(4.2)
(4.2)式,
x
‾
\overline{x}
x是一个常量,(4.2)式相当于是
x
‾
x
1
+
x
‾
x
2
+
⋅
⋅
⋅
+
x
‾
x
m
=
x
‾
(
x
1
+
x
2
+
⋅
⋅
⋅
+
x
m
)
\overline{x} x_1+\overline{x} x_2+···+\overline{x} x_m=\overline{x} (x_1+x_2+···+x_m)
xx1+xx2+⋅⋅⋅+xxm=x(x1+x2+⋅⋅⋅+xm)
证明
∑
i
=
1
m
(
x
i
−
x
‾
)
x
i
=
∑
i
=
1
m
(
x
i
−
x
‾
)
2
\textstyle\sum_{i=1}^m{ \left( {x}_i-\overline{x} \right)x_i} =\textstyle\sum_{i=1}^m{ \left( {x}_i-\overline{x} \right)^2}
∑i=1m(xi−x)xi=∑i=1m(xi−x)2
∑
i
=
1
m
(
x
i
−
x
‾
)
x
i
=
∑
i
=
1
m
(
x
i
2
−
x
‾
x
i
)
(
4.3
)
=
∑
i
=
1
m
(
x
i
2
−
x
‾
x
i
+
x
‾
x
i
−
x
‾
x
i
)
(
4.4
)
=
∑
i
=
1
m
(
x
i
2
−
2
x
‾
x
i
+
x
‾
x
i
)
(
4.5
)
=
∑
i
=
1
m
(
x
i
2
−
2
x
‾
x
i
)
+
∑
i
=
1
m
(
x
‾
x
i
)
(
4.6
)
=
∑
i
=
1
m
(
x
i
2
−
2
x
‾
x
i
)
+
x
‾
∑
i
=
1
m
(
x
i
)
(
4.7
)
=
∑
i
=
1
m
(
x
i
2
−
2
x
‾
x
i
)
+
x
‾
⋅
m
x
‾
(
4.8
)
=
∑
i
=
1
m
(
x
i
2
−
2
x
‾
x
i
)
+
m
x
‾
2
(
4.9
)
=
∑
i
=
1
m
(
x
i
2
−
2
x
‾
x
i
)
+
∑
i
=
1
m
x
‾
2
(
4.10
)
=
∑
i
=
1
m
(
x
i
2
−
2
x
‾
x
i
+
x
‾
2
)
(
4.11
)
=
∑
i
=
1
m
(
x
i
−
x
‾
)
2
(
4.12
)
\begin{aligned} \displaystyle\sum_{i=1}^m{ \left( {x}_i-\overline{x} \right)x_i} &=\displaystyle\sum_{i=1}^m{ \left( {x}_i^2-\overline{x} x_i \right)} &{(4.3)} \\ &=\displaystyle\sum_{i=1}^m{ \left( {x}_i^2-\overline{x} x_i + \overline{x} x_i - \overline{x} x_i \right)} &{(4.4)} \\ &=\displaystyle\sum_{i=1}^m{ \left( {x}_i^2-2 \overline{x} x_i + \overline{x} x_i \right)} &{(4.5)} \\ &=\displaystyle\sum_{i=1}^m{ \left( {x}_i^2-2 \overline{x} x_i \right)} + \displaystyle\sum_{i=1}^m{ \left( \overline{x} x_i \right)} &{(4.6)} \\ &=\displaystyle\sum_{i=1}^m{ \left( {x}_i^2-2 \overline{x} x_i \right)} + \overline{x}\displaystyle\sum_{i=1}^m{ \left( x_i \right)} &{(4.7)} \\ &=\displaystyle\sum_{i=1}^m{ \left( {x}_i^2-2 \overline{x} x_i \right)} + \overline{x}·m\overline{x} &{(4.8)} \\ &=\displaystyle\sum_{i=1}^m{ \left( {x}_i^2-2 \overline{x} x_i \right)} + m\overline{x}^2 &{(4.9)} \\ &=\displaystyle\sum_{i=1}^m{ \left( {x}_i^2-2 \overline{x} x_i \right)} + \displaystyle\sum_{i=1}^m{ \overline{x}^2 } &{(4.10)} \\ &=\displaystyle\sum_{i=1}^m{ \left( {x}_i^2-2 \overline{x} x_i + \overline{x}^2 \right) } &{(4.11)} \\ &=\displaystyle\sum_{i=1}^m{ \left( {x}_i- \overline{x} \right)^2 } &{(4.12)} \end{aligned}
i=1∑m(xi−x)xi=i=1∑m(xi2−xxi)=i=1∑m(xi2−xxi+xxi−xxi)=i=1∑m(xi2−2xxi+xxi)=i=1∑m(xi2−2xxi)+i=1∑m(xxi)=i=1∑m(xi2−2xxi)+xi=1∑m(xi)=i=1∑m(xi2−2xxi)+x⋅mx=i=1∑m(xi2−2xxi)+mx2=i=1∑m(xi2−2xxi)+i=1∑mx2=i=1∑m(xi2−2xxi+x2)=i=1∑m(xi−x)2(4.3)(4.4)(4.5)(4.6)(4.7)(4.8)(4.9)(4.10)(4.11)(4.12)
证明
∑
i
=
1
m
(
x
i
−
x
‾
)
x
i
=
∑
i
=
i
m
x
i
2
−
m
x
‾
2
\textstyle\sum_{i=1}^m{ \left( {x}_i-\overline{x} \right)x_i} =\textstyle \sum_{i=i}^m{ x_i^2 } -m\overline{x}^2
∑i=1m(xi−x)xi=∑i=imxi2−mx2:
∑
i
=
1
m
(
x
i
−
x
‾
)
x
i
=
∑
i
=
1
m
x
i
2
−
∑
i
=
1
m
x
‾
x
i
(
4.13
)
=
∑
i
=
1
m
x
i
2
−
x
‾
∑
i
=
1
m
x
i
(
4.14
)
=
∑
i
=
1
m
x
i
2
−
x
‾
⋅
m
x
‾
(
4.15
)
=
∑
i
=
1
m
x
i
2
−
m
x
‾
2
(
4.16
)
\begin{aligned} \displaystyle\sum_{i=1}^m{ \left( {x}_i-\overline{x} \right)x_i} &=\displaystyle\sum_{i=1}^m{ {x}_i^2 }-\displaystyle\sum_{i=1}^m{\overline{x} x_i } &{(4.13)} \\ &=\displaystyle\sum_{i=1}^m{ {x}_i^2 }-\overline{x}\displaystyle\sum_{i=1}^m{ x_i } &{(4.14)} \\ &=\displaystyle\sum_{i=1}^m{ {x}_i^2 }-\overline{x}·m\overline{x} &{(4.15)} \\ &=\displaystyle\sum_{i=1}^m{ {x}_i^2 }-m\overline{x}^2 &{(4.16)} \end{aligned}
i=1∑m(xi−x)xi=i=1∑mxi2−i=1∑mxxi=i=1∑mxi2−xi=1∑mxi=i=1∑mxi2−x⋅mx=i=1∑mxi2−mx2(4.13)(4.14)(4.15)(4.16)
结合(4.1)式代入(4.14)可得到(4.15)式。
4.2 如何证明
∑
i
=
1
m
(
x
i
−
x
‾
)
y
i
=
∑
i
=
1
m
(
y
i
−
y
‾
)
x
i
=
∑
i
=
i
m
(
y
i
−
y
‾
)
(
x
i
−
x
‾
)
=
∑
i
=
i
m
x
i
y
i
−
m
x
‾
y
‾
\textstyle \sum_{i=1}^m{\left( x_i-\overline{x} \right)y_i}=\textstyle \sum_{i=1}^m{\left( y_i-\overline{y} \right)x_i} =\textstyle \sum_{i=i}^m{\left( y_i - \overline{y} \right) \left( x_i -\overline{x} \right)} = \textstyle \sum_{i=i}^m{ x_iy_i } -m\overline{x}\overline{y}
∑i=1m(xi−x)yi=∑i=1m(yi−y)xi=∑i=im(yi−y)(xi−x)=∑i=imxiyi−mxy成立?
x
‾
=
1
m
∑
i
=
1
m
x
i
(
4.17
)
y
‾
=
1
m
∑
i
=
1
m
y
i
(
4.18
)
\begin{aligned} \overline{x}= \dfrac{1}{m} \displaystyle \sum_{i=1}^m{x_i} &{(4.17)} \\ \overline{y}= \dfrac{1}{m} \displaystyle \sum_{i=1}^m{y_i} &{(4.18)} \end{aligned}
x=m1i=1∑mxiy=m1i=1∑myi(4.17)(4.18)
证明
∑
i
=
1
m
(
x
i
−
x
‾
)
y
i
=
∑
i
=
1
m
(
y
i
−
y
‾
)
x
i
\textstyle \sum_{i=1}^m{\left( x_i-\overline{x} \right)y_i}=\textstyle \sum_{i=1}^m{\left( y_i-\overline{y} \right)x_i}
∑i=1m(xi−x)yi=∑i=1m(yi−y)xi:
∑
i
=
1
m
(
x
i
−
x
‾
)
y
i
=
∑
i
=
1
m
(
x
i
y
i
−
x
‾
y
i
)
(
4.19
)
=
∑
i
=
1
m
x
i
y
i
−
∑
i
=
1
m
x
‾
y
i
(
4.20
)
=
∑
i
=
1
m
x
i
y
i
−
x
‾
⋅
∑
i
=
1
m
y
i
(
4.21
)
=
∑
i
=
1
m
x
i
y
i
−
(
1
m
∑
i
=
1
m
x
i
)
⋅
(
m
y
‾
)
(
4.22
)
=
∑
i
=
1
m
x
i
y
i
−
y
‾
∑
i
=
1
m
x
i
(
4.23
)
=
∑
i
=
1
m
x
i
y
i
−
∑
i
=
1
m
y
‾
x
i
(
4.24
)
=
∑
i
=
1
m
(
x
i
y
i
−
y
‾
x
i
)
(
4.25
)
=
∑
i
=
1
m
(
y
i
−
y
‾
)
x
i
(
4.26
)
\begin{aligned} \displaystyle \sum_{i=1}^m{\left( x_i-\overline{x} \right)y_i} &=\displaystyle\sum_{i=1}^m{ \left( x_iy_i-\overline{x}y_i \right)} &{(4.19)} \\ &=\displaystyle\sum_{i=1}^m{ x_iy_i}-\displaystyle\sum_{i=1}^m{ \overline{x}y_i } &{(4.20)} \\ &=\displaystyle\sum_{i=1}^m{ x_iy_i}-\overline{x}·\displaystyle\sum_{i=1}^m{ y_i } &{(4.21)} \\ &=\displaystyle\sum_{i=1}^m{ x_iy_i}-\left( \dfrac{1}{m} \displaystyle \sum_{i=1}^m{x_i} \right) · \left( m \overline{y} \right) &{(4.22)} \\ &=\displaystyle\sum_{i=1}^m{ x_iy_i}-\overline{y}\displaystyle \sum_{i=1}^m{x_i} &{(4.23)} \\ &=\displaystyle\sum_{i=1}^m{ x_iy_i}-\displaystyle \sum_{i=1}^m{\overline{y}x_i} &{(4.24)} \\ &=\displaystyle\sum_{i=1}^m{ \left( x_iy_i- \overline{y}x_i \right)} &{(4.25)} \\ &=\displaystyle \sum_{i=1}^m{\left( y_i-\overline{y} \right)x_i} &{(4.26)} \end{aligned}
i=1∑m(xi−x)yi=i=1∑m(xiyi−xyi)=i=1∑mxiyi−i=1∑mxyi=i=1∑mxiyi−x⋅i=1∑myi=i=1∑mxiyi−(m1i=1∑mxi)⋅(my)=i=1∑mxiyi−yi=1∑mxi=i=1∑mxiyi−i=1∑myxi=i=1∑m(xiyi−yxi)=i=1∑m(yi−y)xi(4.19)(4.20)(4.21)(4.22)(4.23)(4.24)(4.25)(4.26)
将(4.17)和(4.18)代入(4.21)可得到(4.22)。
注意:
∑
i
=
1
m
x
i
y
i
/
=
x
i
∑
i
=
1
m
y
i
\textstyle \sum_{i=1}^m{x_iy_i} \mathrlap{\,/}{=} x_i\textstyle \sum_{i=1}^m{y_i}
∑i=1mxiyi/=xi∑i=1myi因为
x
i
x_i
xi不是常量,
∑
i
=
1
m
x
i
y
i
\textstyle \sum_{i=1}^m{x_iy_i}
∑i=1mxiyi表示的是两个变量
x
i
x_i
xi和
y
i
y_i
yi乘积的和,计算顺序为先乘后加。而
x
i
∑
i
=
1
m
y
i
x_i\textstyle \sum_{i=1}^m{y_i}
xi∑i=1myi是对变量
y
i
y_i
yi求和之后乘以变量
x
i
x_i
xi。如果
x
i
x_i
xi为常量等式才成立。
证明
∑
i
=
1
m
(
x
i
−
x
‾
)
y
i
=
∑
i
=
i
m
(
y
i
−
y
‾
)
(
x
i
−
x
‾
)
\textstyle \sum_{i=1}^m{\left( x_i-\overline{x} \right)y_i} =\textstyle \sum_{i=i}^m{\left( y_i - \overline{y} \right) \left( x_i -\overline{x} \right)}
∑i=1m(xi−x)yi=∑i=im(yi−y)(xi−x):
∑
i
=
i
m
(
y
1
−
y
‾
)
(
x
i
−
x
‾
)
=
∑
i
=
i
m
(
x
i
y
i
−
x
‾
y
i
−
x
i
y
‾
+
x
y
‾
)
(
4.27
)
=
∑
i
=
i
m
(
x
i
−
x
‾
)
y
i
−
∑
i
=
i
m
(
x
i
y
‾
)
+
∑
i
=
i
m
(
x
y
‾
)
(
4.28
)
=
∑
i
=
i
m
(
x
i
−
x
‾
)
y
i
−
y
‾
∑
i
=
i
m
(
x
i
)
+
y
‾
∑
i
=
i
m
(
x
‾
)
(
4.29
)
=
∑
i
=
i
m
(
x
i
−
x
‾
)
y
i
−
m
x
y
‾
+
−
m
x
y
‾
(
4.30
)
=
∑
i
=
i
m
(
x
i
−
x
‾
)
y
i
(
4.31
)
\begin{aligned} \displaystyle \sum_{i=i}^m{\left( y_1 - \overline{y} \right) \left( x_i -\overline{x} \right)} &=\displaystyle \sum_{i=i}^m{\left( x_iy_i -\overline{x}y_i - x_i\overline{y} +\overline{xy} \right)} &{(4.27)} \\&=\displaystyle \sum_{i=i}^m{\left( x_i -\overline{x} \right)y_i} -\displaystyle \sum_{i=i}^m{\left( x_i\overline{y} \right) }+\displaystyle \sum_{i=i}^m{\left(\overline{xy} \right)} &{(4.28)} \\&=\displaystyle \sum_{i=i}^m{\left( x_i -\overline{x} \right)y_i} -\overline{y}\displaystyle \sum_{i=i}^m{\left( x_i \right) }+\overline{y}\displaystyle \sum_{i=i}^m{\left(\overline{x} \right)} &{(4.29)} \\&=\displaystyle \sum_{i=i}^m{\left( x_i -\overline{x} \right)y_i} -m\overline{xy}+-m\overline{xy} &{(4.30)} \\&=\displaystyle \sum_{i=i}^m{\left( x_i -\overline{x} \right)y_i} &{(4.31)} \end{aligned}
i=i∑m(y1−y)(xi−x)=i=i∑m(xiyi−xyi−xiy+xy)=i=i∑m(xi−x)yi−i=i∑m(xiy)+i=i∑m(xy)=i=i∑m(xi−x)yi−yi=i∑m(xi)+yi=i∑m(x)=i=i∑m(xi−x)yi−mxy+−mxy=i=i∑m(xi−x)yi(4.27)(4.28)(4.29)(4.30)(4.31)
将(4.1)式和(4.17)式代入(4.29),可得到(4.30)。
证明
∑
i
=
1
m
(
x
i
−
x
‾
)
y
i
=
∑
i
=
i
m
x
i
y
i
−
m
x
‾
y
‾
\textstyle \sum_{i=1}^m{\left( x_i-\overline{x} \right)y_i} = \textstyle \sum_{i=i}^m{ x_iy_i } -m\overline{x}\overline{y}
∑i=1m(xi−x)yi=∑i=imxiyi−mxy:结合(4.18)式和(4.21)式,即可推导出该结果。
4.3 为什么
J
(
a
,
b
)
=
1
2
m
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
2
J_{(a,b)} =\dfrac{1}{2m} \textstyle\sum_{i=1}^m{\left( ax_i+b-y_i \right)^2}
J(a,b)=2m1∑i=1m(axi+b−yi)2对a 求导之后是
1
m
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
x
i
\dfrac{1}{m} \textstyle \sum_{i=1}^m{\left( ax_i+b-y_i\right) x_i}
m1∑i=1m(axi+b−yi)xi,而对b 求导之后是
1
m
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
\dfrac{1}{m} \textstyle \sum_{i=1}^m{\left( ax_i+b-y_i\right)}
m1∑i=1m(axi+b−yi)?
在
E
(
a
,
b
)
E(a,b)
E(a,b)函数上对a和b求导的解法和该解法相类似,不赘述。
J
(
a
,
b
)
=
1
2
m
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
2
(
4.32
)
=
1
2
m
∑
i
=
1
m
(
x
i
2
a
2
+
2
(
b
−
y
i
)
x
i
a
+
(
b
−
y
i
)
2
)
(
4.33
)
=
1
2
m
∑
i
=
1
m
(
b
2
+
2
(
a
x
i
−
y
i
)
b
+
(
a
x
i
−
y
i
)
2
)
(
4.34
)
\begin{aligned} J\left( a,b \right) &= \dfrac{1}{2m} \displaystyle \sum_{i=1}^m{ \left( ax_i+b - y_i \right) ^2 } &{(4.32)} \\ &= \dfrac{1}{2m} \displaystyle \sum_{i=1}^m{\left( x_i^2a^2 + 2 \left(b-y_i \right)x_ia + \left(b-y_i \right)^2 \right)} &{(4.33)} \\ &= \dfrac{1}{2m} \displaystyle \sum_{i=1}^m{\left( b^2 + 2 \left(ax_i-y_i \right)b + \left(ax_i-y_i \right)^2 \right)} &{(4.34)} \end{aligned}
J(a,b)=2m1i=1∑m(axi+b−yi)2=2m1i=1∑m(xi2a2+2(b−yi)xia+(b−yi)2)=2m1i=1∑m(b2+2(axi−yi)b+(axi−yi)2)(4.32)(4.33)(4.34)
使用(4.33)式,对a求导;使用(4.34)式对b求导。
∂
J
(
a
,
b
)
∂
a
=
1
2
m
∑
i
=
1
m
(
2
x
i
2
a
+
2
(
b
−
y
i
)
x
i
+
0
)
(
4.35
)
=
1
2
m
∑
i
=
1
m
2
x
i
(
x
i
a
+
(
b
−
y
i
)
)
(
4.36
)
=
1
m
∑
i
=
1
m
x
i
(
x
i
a
+
b
−
y
i
)
(
4.37
)
=
1
m
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
x
i
(
4.38
)
∂
J
(
a
,
b
)
∂
b
=
1
2
m
∑
i
=
1
m
(
2
b
+
2
(
a
x
i
−
y
i
)
+
0
)
(
4.39
)
=
1
2
m
∑
i
=
1
m
2
x
i
(
x
i
a
+
(
b
−
y
i
)
)
(
4.40
)
=
1
m
∑
i
=
1
m
x
i
(
x
i
a
+
b
−
y
i
)
(
4.41
)
=
1
m
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
x
i
(
4.42
)
\begin{aligned} \dfrac{\partial J_{(a,b)}}{\partial a} &=\dfrac{1}{2m} \displaystyle \sum_{i=1}^m{\left( 2x_i^2a + 2 \left(b-y_i \right)x_i + 0 \right)} &{(4.35)} \\&=\dfrac{1}{2m} \displaystyle \sum_{i=1}^m{ 2x_i \left( x_ia + \left(b-y_i \right) \right) } &{(4.36)} \\&=\dfrac{1}{m} \displaystyle \sum_{i=1}^m{ x_i \left( x_ia + b-y_i \right) } &{(4.37)} \\&=\dfrac{1}{m} \displaystyle \sum_{i=1}^m{\left( ax_i+b-y_i\right) x_i} &{(4.38)} \end{aligned} \\ \begin{aligned} \dfrac{\partial J_{(a,b)}}{\partial b} &= \dfrac{1}{2m} \displaystyle \sum_{i=1}^m{\left( 2b + 2 \left(ax_i-y_i \right) + 0 \right)} &{(4.39)} \\&=\dfrac{1}{2m} \displaystyle \sum_{i=1}^m{ 2x_i \left( x_ia + \left(b-y_i \right) \right) } &{(4.40)} \\&=\dfrac{1}{m} \displaystyle \sum_{i=1}^m{ x_i \left( x_ia + b-y_i \right) } &{(4.41)} \\&=\dfrac{1}{m} \displaystyle \sum_{i=1}^m{\left( ax_i+b-y_i\right) x_i} &{(4.42)} \end{aligned}
∂a∂J(a,b)=2m1i=1∑m(2xi2a+2(b−yi)xi+0)=2m1i=1∑m2xi(xia+(b−yi))=m1i=1∑mxi(xia+b−yi)=m1i=1∑m(axi+b−yi)xi(4.35)(4.36)(4.37)(4.38)∂b∂J(a,b)=2m1i=1∑m(2b+2(axi−yi)+0)=2m1i=1∑m2xi(xia+(b−yi))=m1i=1∑mxi(xia+b−yi)=m1i=1∑m(axi+b−yi)xi(4.39)(4.40)(4.41)(4.42)
4.4 sklearn.metrics.r2_score的公式及变形推导
基础知识:
总体平方和(Total Sum of Squares):
T
S
S
=
∑
i
=
1
m
(
y
i
−
y
‾
)
2
TSS= \textstyle \sum_{i=1}^m{ \left( y_i-\overline{y} \right)^2}
TSS=∑i=1m(yi−y)2(实际值与均值的差值的平方和)
回归平方和(Explained Sum of Squares):
E
S
S
=
∑
i
=
1
m
(
y
′
−
y
‾
)
2
ESS=\textstyle \sum_{i=1}^m{ \left( y'-\overline{y} \right)^2}
ESS=∑i=1m(y′−y)2(预测值与均值的差值的平方和)
残差平方和(Residual Sum of Squares):
R
S
S
=
∑
i
=
1
m
(
y
i
−
y
′
)
2
RSS=\textstyle \sum_{i=1}^m{ \left( y_i-y' \right)^2}
RSS=∑i=1m(yi−y′)2(实际值与预测值的差值的平方和)
T
S
S
=
E
S
S
+
R
S
S
TSS=ESS+RSS
TSS=ESS+RSS
均方差(Mean Square Error):
M
S
E
=
1
m
∑
i
=
1
m
(
y
i
−
y
′
)
2
=
1
m
R
S
S
MSE=\dfrac{1}{m} \textstyle \sum_{i=1}^m{ \left( y_i-y' \right)^2}=\dfrac{1}{m}RSS
MSE=m1∑i=1m(yi−y′)2=m1RSS
y的方差(Variance):
v
a
r
y
=
1
m
∑
i
=
1
m
(
y
i
−
y
‾
)
2
=
1
m
T
S
S
var_y=\dfrac{1}{m} \textstyle \sum_{i=1}^m{ \left( y_i-\overline{y} \right)^2}=\dfrac{1}{m}TSS
vary=m1∑i=1m(yi−y)2=m1TSS
x的方差(Variance):
v
a
r
x
=
1
m
∑
i
=
1
m
(
x
i
−
x
‾
)
2
var_x=\dfrac{1}{m} \textstyle \sum_{i=1}^m{ \left( x_i-\overline{x} \right)^2}
varx=m1∑i=1m(xi−x)2
标准差(Standard Deviation):
s
t
d
=
v
a
r
std=\sqrt{var}
std=var
R
2
=
1
−
R
S
S
T
S
S
(
残
差
平
方
和
与
总
体
平
方
和
的
比
值
)
=
1
−
M
S
E
v
a
r
y
(
均
方
差
和
y
i
的
方
差
的
比
值
)
=
a
s
t
d
(
x
i
)
s
t
d
(
y
i
)
(
直
线
系
数
a
乘
以
x
i
和
y
i
的
标
准
差
的
比
值
)
\begin{aligned} R^2 &=1-\dfrac{RSS}{TSS}(残差平方和与总体平方和的比值) \\&=1-\dfrac{MSE}{var_y}(均方差和y_i的方差的比值) \\&=a\dfrac{std(x_i)}{std(y_i)}(直线系数a乘以x_i和y_i的标准差的比值) \end{aligned}
R2=1−TSSRSS(残差平方和与总体平方和的比值)=1−varyMSE(均方差和yi的方差的比值)=astd(yi)std(xi)(直线系数a乘以xi和yi的标准差的比值)
对
R
2
R^2
R2从上到下推导:
(4.43)~(4.45)证明:
R
2
=
1
−
R
S
S
T
S
S
=
1
−
M
S
E
v
a
r
y
\begin{aligned} R^2=1-\dfrac{RSS}{TSS}=1-\dfrac{MSE}{var_y} \end{aligned}
R2=1−TSSRSS=1−varyMSE
(4.46)~(4.54)证明:
R
2
=
1
−
R
S
S
T
S
S
=
a
s
t
d
(
x
i
)
s
t
d
(
y
i
)
\begin{aligned} R^2=1-\dfrac{RSS}{TSS} =a\dfrac{std(x_i)}{std(y_i)} \end{aligned}
R2=1−TSSRSS=astd(yi)std(xi)
注:
y
′
=
a
x
i
+
b
y'=ax_i+b
y′=axi+b代入(4.48),
b
=
y
‾
−
a
x
‾
b=\overline{y}-a\overline{x}
b=y−ax代入(4.49)
R
2
=
1
−
R
S
S
T
S
S
(
4.43
)
=
1
−
1
m
R
S
S
1
m
T
S
S
(
4.44
)
=
1
−
M
S
E
v
a
r
y
(
4.45
)
=
T
S
S
−
R
S
S
T
S
S
(
4.46
)
=
E
S
S
T
S
S
(
4.47
)
=
∑
i
=
1
m
(
y
′
−
y
‾
)
2
∑
i
=
1
m
(
y
i
−
y
‾
)
2
(
4.48
)
=
∑
i
=
1
m
(
a
x
i
+
b
−
y
‾
)
2
∑
i
=
1
m
(
y
i
−
y
‾
)
2
(
4.49
)
=
∑
i
=
1
m
(
a
x
i
+
(
y
‾
−
a
x
‾
)
−
y
‾
)
2
∑
i
=
1
m
(
y
i
−
y
‾
)
2
(
4.50
)
=
∑
i
=
1
m
(
a
x
i
−
a
x
‾
)
2
∑
i
=
1
m
(
y
i
−
y
‾
)
2
(
4.51
)
=
a
2
∑
i
=
1
m
(
x
i
−
x
‾
)
2
∑
i
=
1
m
(
y
i
−
y
‾
)
2
(
4.52
)
=
a
2
1
m
∑
i
=
1
m
(
x
i
−
x
‾
)
2
1
m
∑
i
=
1
m
(
y
i
−
y
‾
)
2
(
4.53
)
=
a
2
v
a
r
(
x
i
)
v
a
r
(
y
i
)
(
4.54
)
\begin{aligned} R^2 &=1-\dfrac{RSS}{TSS} &{(4.43)} \\&=1-\dfrac{\dfrac{1}{m}RSS}{\dfrac{1}{m}TSS} &{(4.44)} \\&=1-\dfrac{MSE}{var_y} &{(4.45)} \\&=\dfrac{TSS-RSS}{TSS} &{(4.46)} \\&=\dfrac{ESS}{TSS} &{(4.47)} \\&=\dfrac{\displaystyle \sum_{i=1}^m{ \left( y'-\overline{y} \right)^2}}{\displaystyle \sum_{i=1}^m{ \left( y_i-\overline{y} \right)^2}} &{(4.48)} \\&=\dfrac{\displaystyle \sum_{i=1}^m{ \left( ax_i+b-\overline{y} \right)^2}}{\displaystyle \sum_{i=1}^m{ \left( y_i-\overline{y} \right)^2}} &{(4.49)} \\&=\dfrac{\displaystyle \sum_{i=1}^m{ \left( ax_i+\left( \overline{y}-a\overline{x}\right)-\overline{y} \right)^2}}{\displaystyle \sum_{i=1}^m{ \left( y_i-\overline{y} \right)^2}} &{(4.50)} \\&=\dfrac{\displaystyle \sum_{i=1}^m{ \left( ax_i-a\overline{x} \right)^2}}{\displaystyle \sum_{i=1}^m{ \left( y_i-\overline{y} \right)^2}} &{(4.51)} \\&=\dfrac{a^2\displaystyle \sum_{i=1}^m{ \left( x_i-\overline{x} \right)^2}}{\displaystyle \sum_{i=1}^m{ \left( y_i-\overline{y} \right)^2}} &{(4.52)} \\&=a^2\dfrac{ \dfrac{1}{m} \displaystyle \sum_{i=1}^m{ \left( x_i-\overline{x} \right)^2}}{\dfrac{1}{m}\displaystyle \sum_{i=1}^m{ \left( y_i-\overline{y} \right)^2}} &{(4.53)} \\&=a^2\dfrac{var(x_i)}{var(y_i)} &{(4.54)} \end{aligned}
R2=1−TSSRSS=1−m1TSSm1RSS=1−varyMSE=TSSTSS−RSS=TSSESS=i=1∑m(yi−y)2i=1∑m(y′−y)2=i=1∑m(yi−y)2i=1∑m(axi+b−y)2=i=1∑m(yi−y)2i=1∑m(axi+(y−ax)−y)2=i=1∑m(yi−y)2i=1∑m(axi−ax)2=i=1∑m(yi−y)2a2i=1∑m(xi−x)2=a2m1i=1∑m(yi−y)2m1i=1∑m(xi−x)2=a2var(yi)var(xi)(4.43)(4.44)(4.45)(4.46)(4.47)(4.48)(4.49)(4.50)(4.51)(4.52)(4.53)(4.54)
5 参考:
机器学习-周志华-P54
语雀Latex:https://www.yuque.com/yuque/gpvawt/brzicb
符号Katex:https://katex.org/docs/supported.html
小小福利:第4部分公式的推导,可以点击该链接下载相关Markdown文档。














![[附源码]计算机毕业设计JAVA基于web旅游网站的设计与实现](https://img-blog.csdnimg.cn/507ed4bd98ba4f22861e52a1ffb57da8.png)