AVL树

为避免BST树退化成链表的极端情况， AVL 树应运而生。

平衡因子取值（-1，0，1）
查找、插入、删除操作和BST保持一致，但是需要处理失衡（平衡因子不满足取值范围）的情况。

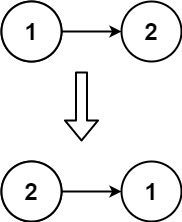
左旋

复杂情况：

右旋

复杂情况：

左旋右旋的4种情况

LL 型

插入节点3导致 14节点失衡。插入位置是14节点的左孩子的左子树上：

RR 型

插入节点 17 导致 5节点失衡。插入位置是5节点的右孩子的右子树上：

LR 型

插入节点6，导致节点9失衡，插入位置是在9节点左孩子的右子树上：

RL 型

插入节点8，导致节点5失衡，插入位置是在5节点右孩子的左子树上：

实际插入时怎么判断是那种类型？

根据插入位置是在哪个孩子的哪个子树上确定， 也可以通过平衡因子判断，用平衡因子判断更加常见：

插入时注意事项

如果同时多个祖先节点失衡，只需要调整距离插入节点最近的失衡节点，其他失衡节点会自然平衡.

删除节点

需要沿着祖先依次向上检查和调整