LeetCode 热题 100 题解记录
哈希
1. 两数之和
利用Map判断是否包含需要的值来求解
49. 字母异位词分组
- 初始化哈希表:
- 创建一个哈希表
map,用于存储分组结果。键为排序后的字符串,值为原字符串列表。- 遍历输入字符串数组:
- 对于每个字符串,先将其转换为字符数组并进行排序。
- 将排序后的字符数组转换回字符串,作为哈希表的键。
- 分组存储:
- 如果哈希表中不存在该键,则创建一个新的列表。
- 将当前字符串添加到对应的列表中,并更新哈希表。
- 返回结果:
- 将哈希表中的所有值(即分组后的列表)转换为一个列表并返回。
128. 最长连续序列
- 将数组元素存入HashSet:
- 使用
HashSet存储数组中的所有元素,以便于后续进行 O(1) 时间复杂度的查找操作。- 初始化最长连续序列长度:
- 初始化一个变量
longestStreak用于记录最长连续序列的长度,初始值为 0。- 遍历HashSet中的每个元素:
- 对于每个元素
num,检查num - 1是否存在于HashSet中。如果不存在,说明num是一个新的连续序列的起点。- 计算当前连续序列的长度:
- 从当前元素
num开始,检查num + 1是否存在于HashSet中,如果存在则继续增加序列长度,直到找不到下一个连续数字为止。- 更新最长连续序列长度:
- 在每次计算完一个连续序列的长度后,更新
longestStreak为当前最长序列长度和之前记录的最长序列长度中的较大值。- 返回结果:
- 遍历结束后,返回
longestStreak,即最长连续序列的长度。
双指针
283. 移动零
解法一:双指针
- 初始化指针:
left和right:两个指针,初始都指向数组的起始位置。- 遍历数组:
- 使用
right指针遍历整个数组。- 当
nums[right]不为零时,交换nums[left]和nums[right]的值,并将left指针右移一位。- 无论是否交换,
right指针都右移一位,继续检查下一个元素。- 填充零:
- 遍历完成后,所有非零元素已经按顺序排列在数组的前面,从索引
left到n-1的位置填充零。解法二:两次遍历
- 第一次遍历将所有非零元素按顺序移动到数组的前面。
- 第二次遍历将剩余的位置填充为零。
11. 盛最多水的容器
- 初始化指针和变量:
left指向数组的起始位置。right指向数组的末尾位置。maxArea用于记录最大的容器容量。- 循环遍历:
- 当
left小于right时:
- 计算当前容器的容量
area,即min(height[left], height[right]) * (right - left)。- 更新
maxArea为当前容量和之前记录的最大容量中的较大值。- 如果
height[left]小于等于height[right],则左指针left向右移动一位;否则,右指针right向左移动一位。- 返回结果:
- 循环结束后,
maxArea即为最大容器容量。
15. 三数之和
- 对原数组进行排序
- 轮询数组
- 若当前值等于前一值,则跳过本次循环
- 利用双指针(left = i + 1, right = nums.length - 1)计算三数之和
- sum > 0 则 left++, sum < 0 则 right–
- 等于0则记录当前组合,并排除重复元素
42. 接雨水
- 找到最高的位置及高度
- 分别计算左右两边雨水量
滑动窗口
3. 无重复字符的最长子串
- 初始化变量:
res:用于记录最长无重复字符子串的长度,初始值为0。start:滑动窗口的左边界,初始值为0。last:一个长度为128的数组,用于记录每个字符最后一次出现的位置。数组下标对应字符的ASCII码值。- 遍历字符串:
- 使用一个循环遍历字符串
s的每一个字符,循环变量i表示当前字符的位置。- 获取当前字符的ASCII码:
int index = s.charAt(i);获取当前字符的ASCII码值,作为数组last的下标。- 更新滑动窗口的左边界:
start = Math.max(start, last[index]);如果当前字符之前出现过,更新左边界start到重复字符的下一个位置。这里使用Math.max是为了确保start不会回退。- 更新最长子串长度:
res = Math.max(res, i - start + 1);计算当前窗口的长度,并更新res为当前最长子串长度和之前记录的最长子串长度中的较大值。- 更新字符的最后出现位置:
last[index] = i + 1;更新当前字符的最后出现位置为当前位置加1(加1是为了避免初始值0的影响)。- 返回结果:
- 循环结束后,
res即为最长无重复字符子串的长度,返回res。
438. 找到字符串中所有字母异位词
- 初始化变量和边界检查:
- 获取字符串
s和p的长度,分别存储在sLength和pLength中。- 创建一个结果列表
res用于存储符合条件的子串起始索引。- 如果
s的长度小于p,则不可能存在符合条件的子串,直接返回空列表。- 计数数组初始化:
- 创建两个长度为26的整型数组
sCount和pCount,用于记录每个字母出现的次数。- 遍历
pLength次,分别统计目标字符串p中每个字母的出现次数存入pCount,同时统计主字符串s前pLength个字符的出现次数存入sCount。- 检查初始窗口:
- 使用
Arrays.equals方法比较sCount和pCount是否相同。- 如果相同,说明初始窗口
[0, pLength-1]是一个字母异位词,将起始索引0添加到结果列表res中。- 滑动窗口遍历:
- 从索引
pLength开始,逐步向右滑动窗口,直到遍历完整个字符串s。- 在每一步中,将新进入窗口的字符的计数加一,同时将离开窗口的字符的计数减一,以维护当前窗口的字母频率。
- 每次更新后,比较
sCount和pCount是否相同:
- 如果相同,说明当前窗口是一个字母异位词,记录窗口的起始索引
i - pLength + 1到结果列表res中。- 返回结果:
- 遍历完成后,返回结果列表
res,其中包含所有符合条件的子串起始索引。
子串
560. 和为 K 的子数组(不熟悉,需注重复习)
- 初始化变量和数据结构:
- 使用一个
HashMap来存储前缀和及其出现的次数。- 初始化当前前缀和
sum为 0。- 初始化满足条件的子数组个数
count为 0。- 在
map中预先放入一个键值对(0, 1),表示存在一个前缀和为 0 的情况,这样可以处理数组中某个元素本身等于k的情况。- 遍历数组:
- 对于数组中的每一个元素,更新当前的前缀和
sum。- 检查前缀和:
- 检查
map中是否存在键sum - k:
- 如果存在,说明从之前的某个位置到当前位置的子数组和为
k。- 累加
map.get(sum - k)到count,因为map.get(sum - k)表示有多少个前缀和等于sum - k,每个这样的前缀和都可以和当前的前缀和sum组成一个和为k的子数组。- 更新前缀和计数:
- 将当前的前缀和
sum及其出现的次数更新到map中。- 返回结果:
- 遍历结束后,返回
count,即和为k的连续子数组的个数。
239. 滑动窗口最大值
- 初始化:
- 检查输入数组
nums是否有效,以及窗口大小k是否合理。- 计算结果数组
result的长度,即n - k + 1,其中n是nums的长度。- 使用一个双端队列
deque来存储可能成为当前窗口最大值的元素索引。- 遍历数组:
- 对于数组中的每一个元素
nums[i]:
- 移除过期元素:检查队列头部的元素是否已经不在当前窗口范围内(即索引小于
i - k + 1),如果是,则移除它。- 维护队列的单调性:移除队列尾部所有小于当前元素
nums[i]的元素,因为这些元素在当前窗口内不可能成为最大值。- 添加当前元素索引:将当前元素的索引
i加入队列尾部。- 记录当前窗口的最大值:当窗口形成后(即
i >= k - 1),队列头部的元素即为当前窗口的最大值,将其存入结果数组result中。- 返回结果:
- 遍历完成后,返回存储每个滑动窗口最大值的数组
result。
76. 最小覆盖子串
- 初始化计数数组:
- 创建一个长度为 58 的整数数组
cCnt,用于记录目标字符串t中每个字符的出现次数(负数表示缺失)。- 遍历目标字符串
t,将其每个字符的计数减一。- 初始化变量:
start初始化为 0,用于记录最小子串的起始位置。minWindowLength初始化为最大整数值,用于记录最小子串的长度。- 滑动窗口遍历:
- 使用两个指针
left和right分别表示窗口的左右边界,count表示当前窗口中满足条件的字符数。- 遍历字符串
s,扩展右边界right:
- 如果当前字符是目标字符串
t中的字符且计数小于 0,则增加count。- 收缩窗口:
- 当
count等于目标字符串t的长度时,表示当前窗口包含了所有目标字符。- 收缩左边界
left,直到窗口不再包含所有目标字符。- 更新最小子串的长度和起始位置。
- 返回结果:
- 如果找到了满足条件的最小子串,则返回该子串,否则返回空字符串。
普通数组
53. 最大子数组和
用动态规划思想,设
res记录全局最大和(初始化为nums[0]),sum记录当前子数组和(初始化为 0),遍历数组,若sum > 0则sum += num,否则sum = num,每次更新res = max(res, sum),最终返回res。
56. 合并区间
- 边界条件检查:
- 如果输入的区间数组
intervals为空或只有一个区间,直接返回原数组,因为无需合并。- 排序区间:
- 使用
Arrays.sort方法按照每个区间的起始位置对intervals进行升序排序。这一步是关键,因为只有按顺序处理区间,才能有效地合并重叠的区间。- 初始化结果列表:
- 创建一个
ArrayList<int[]>来存储合并后的区间。列表便于动态添加和修改区间。- 遍历并合并区间:
- 遍历排序后的每个区间
p:
- 检查当前区间
p是否与结果列表中最后一个区间有重叠(即p[0] <= ans.get(m - 1)[1])。- 如果有重叠,更新最后一个区间的结束位置为
p[1]和原结束位置的较大值,以确保合并后的区间覆盖所有重叠部分。- 如果没有重叠,直接将当前区间
p添加到结果列表中。- 转换并返回结果:
- 将结果列表转换为二维数组
int[][]并返回,以符合方法的返回类型要求。
189. 轮转数组
- 初始化新数组:
- 创建一个与原数组
nums等长的新数组newArr,用于临时存储轮转后的结果。- 计算并赋值新位置:
- 遍历原数组
nums中的每个元素,计算其在轮转k步后的新位置。- 使用
(i + k) % n计算新位置,确保索引在数组范围内循环。- 将原数组中的元素赋值到新数组的对应位置。
- 复制回原数组:
- 使用
System.arraycopy方法将新数组newArr中的元素复制回原数组nums,完成轮转操作。
238. 除自身以外数组的乘积
- 初始化辅助数组:
- 创建两个辅助数组
L和R,分别用于存储每个元素左侧和右侧所有元素的乘积。- 计算左侧乘积:
- 遍历数组,从左到右填充
L数组。对于每个位置i,L[i]等于nums[i-1] * L[i-1],即当前元素左侧所有元素的乘积。- 计算右侧乘积:
- 遍历数组,从右到左填充
R数组。对于每个位置i,R[i]等于nums[i+1] * R[i+1],即当前元素右侧所有元素的乘积。- 计算最终结果:
- 再次遍历数组,对于每个位置
i,将L[i]和R[i]相乘,得到除nums[i]外其他所有元素的乘积,并存储在answer[i]中。- 返回结果:
- 返回存储最终结果的
answer数组。
41. 缺失的第一个正数
- 放置数字到正确位置:
- 遍历数组,对于每个元素
nums[i]
- 如果
nums[i]在1到length - 1的范围内,并且它没有被放置在正确的位置(即nums[i] != nums[nums[i] - 1]),则将其与它应该在的位置上的元素交换。- 这个过程会持续进行,直到当前位置上的元素已经被正确放置或者不在
1到length - 1的范围内。- 查找缺失的最小正整数:
- 再次遍历数组,寻找第一个不满足
nums[i] == i + 1的位置,该位置的索引加一即为缺失的最小正整数。- 如果所有位置都满足条件,则缺失的最小正整数是
length + 1。
矩阵
73. 矩阵置零
- 初始化变量:
- 获取矩阵的行数
m和列数n。- 创建两个布尔数组
row和col,分别用于记录哪些行和列需要被置为零。- 标记含有零的行和列:
- 遍历整个矩阵,当发现某个元素
matrix[i][j]等于零时,将对应的row[i]和col[j]标记为true,表示第i行和第j列需要被置为零。- 根据标记置零行:
- 遍历所有行,如果某一行被标记为需要置零(
row[i] == true),则将该行的所有元素置为零。- 根据标记置零列:
- 遍历所有列,如果某一列被标记为需要置零(
col[j] == true),则将该列的所有元素置为零。- 优化(可选):
- 为了节省空间,可以利用矩阵的第一行和第一列来记录行和列的标记,而不使用额外的布尔数组。但这需要在处理时额外判断第一行和第一列是否需要置零。
54. 螺旋矩阵
通过设定四个边界变量
left、right、up、down来界定当前螺旋遍历的范围,初始时分别指向矩阵的左、右、上、下边界。在left <= right且up <= down的条件下,按从左到右、从上到下、从右到左、从下到上的顺序依次遍历当前范围内的元素并添加到结果列表res中,每完成一条边的遍历就相应收缩边界,直至所有元素都被遍历完,最终返回结果列表res。
48. 旋转图像
- 水平翻转矩阵:
- 遍历矩阵的上半部分(包括中间行)。
- 对于每一行,将其元素与对应行的对称位置元素进行交换,实现水平翻转。
- 转置矩阵:
- 遍历矩阵的上三角部分(不包括对角线)。
- 对于每个元素
matrix[i][j],将其与matrix[j][i]进行交换,实现矩阵的转置。
240. 搜索二维矩阵 II
- 初始化:
- 检查矩阵是否为空。如果为空,直接返回
false。- 获取矩阵的行数
rows和列数cols。- 初始化当前搜索位置为矩阵的右上角,即
row = 0,col = cols - 1。- 搜索过程:
- 当
row小于rows且col大于等于0时,继续搜索。- 比较当前元素
matrix[row][col]与目标值target:
- 如果相等,返回
true。- 如果当前元素大于目标值,向左移动一列(
col--)。- 如果当前元素小于目标值,向下移动一行(
row++)。- 结束条件:
- 如果搜索过程中行或列超出范围,说明矩阵中不存在目标值,返回
false。
链表
160. 相交链表
- 定义两个指针分别指向两个头节点
- 当两个指针不相等时同时向右移,若某个指针为空则重新指向另外一条链表头节点(保持两个指针距离相交节点是一致的距离)
- 当两个指针相等时则为相交节点
206. 反转链表
- 首先排除一定为当前节点的情况(head为null,或head.next为null)
- 递归调用方法记录结果节点
- 指针反转操作
234. 回文链表
- 处理特殊情况:链表为空或仅有一个节点时,直接判定为回文。
- 使用快慢指针定位中点
- 快指针:每次移动两步(
fast = fast.next.next)。- 慢指针:每次移动一步(
slow = slow.next)。- 反转链表的后半部分:从中点开始,反向连接节点。
- 初始化
prev指针指向null。- 依次将当前节点的
next指针指向prev。- 更新
prev和当前节点指针,继续处理下一个节点。- 处理奇数长度链表:如果快指针未走到链表末尾(说明链表长度为奇数),将慢指针向后移动一步。
- 比较前后两部分链表
- 使用两个指针分别从头节点和中点开始遍历。
- 逐一比较对应节点的值。
- 发现不匹配时立即返回
false。
141. 环形链表
快慢指针节点判断是否会相交
快指针每次走2个节点
慢指针每次走1个节点
快指针 = 慢指针时即为相交
142. 环形链表 II
通过快慢指针节点判断是否会相交来判断是否相交
当相交之后,新记录一个指针节点从头开始找
快指针/慢指针 和 新指针节点 不等时,则 快指针/慢指针 和 新指针节点 同时向后位移1位
相等的位置即为环形链表的入口
21. 合并两个有序链表
通过比较两个有序链表的当前节点值
选择较小的节点作为合并后链表的当前节点,并递归地处理剩余的节点
2. 两数相加
逐位相加并处理进位
- 创建虚拟头节点
- 初始化指针和进位
- 遍历两个链表
- 获取当前节点的值
- 计算总和和进位
- 创建新节点并移动指针
- 移动输入链表的指针
- 返回结果
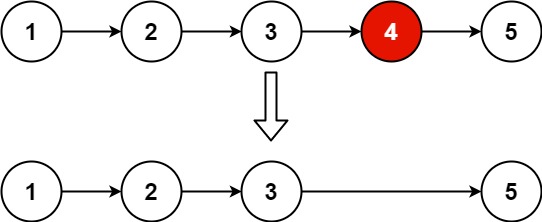
19. 删除链表的倒数第 N 个结点
通过使用双指针技巧
- 先让
fast指针领先slow指针n步- 然后同时移动两个指针,直到
fast到达链表末尾- 此时,
slow指针指向要删除节点的前一个节点
24. 两两交换链表中的节点
使用虚拟头节点和双指针技巧
逐步交换链表中的每两个相邻节点
每次交换过程中,确保前一个节点正确指向新的头节点,并连接后续链表
25. K 个一组翻转链表
记录本次需要反转的尾节点,同时检查当前链表是否有至少k个节点,如果不足k个,则直接返回原链表。
使用三个指针
cur、pre和temp来反转当前的k个节点:cur指向当前处理的节点,pre用于记录反转后的前一个节点,temp暂存下一个待处理的节点。在反转过程中,逐步调整节点的指针方向,完成k个节点的反转。反转完成后,递归地对剩余的链表部分继续进行相同的操作,并将反转后的子链表连接起来。最终返回反转后的链表头节点。
138. 随机链表的复制
- 初始化哈希表:创建哈希表用于缓存节点。
- 遍历链表:递归处理每个节点。
- 复制指针:处理 next 和 random 指针。
- 返回结果:返回复制后的头节点。
148. 排序链表
对链表进行升序排序。采用归并排序,先通过快慢指针找到链表中点将其分割成两部分,递归地对两部分分别排序,再用合并函数将排好序的两部分合并成一个有序链表 。
23. 合并 K 个升序链表
- 分治策略:
- 将K个链表分成两部分,分别递归地合并每一部分,直到只剩下一个链表。
- 使用
devideMerge函数实现分治策略,该函数将lists数组从left到right进行分治合并。- 合并两个链表:
- 使用
mergeTwoLists函数合并两个升序链表。- 比较两个链表的头节点,将较小的节点作为合并后链表的头节点,然后递归地合并剩余的节点。
- 递归合并:
- 在
devideMerge函数中,计算中间位置mid,将lists数组分成两部分,分别递归调用devideMerge函数合并左半部分和右半部分。- 将合并后的左半部分和右半部分再次调用
mergeTwoLists函数合并成一个链表。- 终止条件:
- 如果
left > right,说明没有链表可以合并,返回null。- 如果
left == right,说明只有一个链表,直接返回该链表。
146. LRU 缓存
- 定义缓存容量和数据结构:
- 使用
LinkedHashMap来实现LRU缓存,因为它可以保持插入顺序或访问顺序。- 初始化缓存:
- 在构造函数中,设置缓存的容量,并初始化
LinkedHashMap,将accessOrder参数设置为true,使得每次访问都会更新元素的顺序。- 重写
removeEldestEntry方法:
- 当缓存的大小超过设定的容量时,自动移除最老的元素(即最先插入的元素)。
- 实现
get方法:
- 使用
getOrDefault方法从缓存中获取值,如果键不存在则返回-1。- 实现
put方法:
- 将键值对放入缓存中,如果键已存在,则更新其值。由于
LinkedHashMap的accessOrder为true,每次插入或访问都会自动调整顺序。
二叉树
94. 二叉树的中序遍历
遍历顺序示例:
1 / \ 2 3 / \ \ 4 5 6
遍历方式 访问顺序 示例结果 前序 根 → 左 → 右 [1, 2, 4, 5, 3, 6]中序 左 → 根 → 右 [4, 2, 5, 1, 3, 6]后序 左 → 右 → 根 [4, 5, 2, 6, 3, 1]
104. 二叉树的最大深度
- 分别递归计算左侧和右侧深度
- 取左侧和右侧深度最大值 + 1即为二叉树最大深度
226. 翻转二叉树
经典翻转,可以用递归或者使用额外维护的栈来进行翻转
101. 对称二叉树
- 检查根节点是否为空:
- 如果二叉树的根节点
root为空,按照定义,认为这是一棵对称二叉树,直接返回true。- 调用辅助方法比较子树:
- 使用辅助方法
check比较根节点的左子树 (root.left) 和右子树 (root.right) 是否互为镜像。如果这两部分对称,则整棵树是对称的。- 辅助方法的逻辑:
- 两个节点都为空:如果
p和q都为空,说明当前子树对称,返回true。- 其中一个节点为空:如果
p和q中只有一个为空,说明不对称,返回false。- 节点值及子树对称性:
- 检查当前节点
p和q的值是否相等。- 递归检查
p的左子树与q的右子树是否对称。- 递归检查
p的右子树与q的左子树是否对称。- 只有当以上条件都满足时,才认为
p和q对称,返回true;否则,返回false。
543. 二叉树的直径
通过递归遍历每个节点,计算其左右子树的深度,并在过程中更新最大直径,最终得到二叉树的直径。
- 初始化结果变量:
- 定义一个整数变量
res用于存储二叉树的最大直径。- 计算二叉树的直径:
- 调用辅助函数
getDepth计算以根节点为根的子树深度,并在过程中更新最大直径。- 辅助函数
getDepth的逻辑:
- 如果当前节点为空,返回深度0。
- 递归计算左子树的深度。
- 递归计算右子树的深度。
- 更新最大直径
res,直径等于左子树深度加右子树深度。- 返回当前节点的深度,即左右子树深度的较大值加1。
102. 二叉树的层序遍历
借助队列来辅助完成:
- 首先将根节点入队,然后进入循环
- 每次循环处理当前队列中所有节点,依次将这些节点的值存入当前层的列表,并将它们的左右子节点(若存在)依次入队
- 每处理完一层节点后,将该层的节点值列表添加到结果集中,直到队列为空,最终返回包含所有层节点值的列表集合
108. 将有序数组转换为二叉搜索树
每次递归都将数组分成两部分,分别构建左右子树,最终形成一棵高度平衡的二叉搜索树。
- 确定中间元素作为根节点:
- 选择数组的中间元素作为当前子树的根节点,这样可以确保左右子树的节点数量尽可能平衡,从而保证树的高度平衡。
- 递归构建左子树和右子树:
- 对数组的左半部分递归调用构建函数,生成左子树。
- 对数组的右半部分递归调用构建函数,生成右子树。
- 递归终止条件:
- 当子数组的左边界超过右边界时,返回
null,表示没有节点。
98. 验证二叉搜索树
- 定义辅助方法:
- 创建一个辅助方法
isValidBST(TreeNode node, long lower, long upper),用于递归判断以node为根的子树是否满足 BST 的性质。- 参数
lower和upper分别表示当前节点值的下界和上界。- 递归终止条件:
- 如果当前节点
node为空,返回true,因为空树被认为是有效的 BST。- 验证当前节点:
- 检查当前节点的值
node.val是否在(lower, upper)的范围内。- 如果不在范围内,返回
false,因为不满足 BST 的性质。- 递归检查子树:
- 对左子树进行递归调用,更新上界为当前节点的值
node.val。- 对右子树进行递归调用,更新下界为当前节点的值
node.val。- 只有当左子树和右子树都满足 BST 的性质时,整个树才是有效的 BST。
- 初始调用:
- 在主方法
isValidBST(TreeNode root)中,初始调用辅助方法,设置初始的下界为极小值Long.MIN_VALUE,上界为极大值Long.MAX_VALUE,以覆盖所有可能的整数值。
230. 二叉搜索树中第 K 小的元素
二叉搜索树(BST)的中序遍历可以得到一个升序的节点值序列。利用这一特性,可以通过中序遍历来找到第 k 小的元素。以下是具体步骤:
- 初始化栈:
- 使用一个栈来辅助进行中序遍历。
- 遍历左子树:
- 从根节点开始,将当前节点及其所有左子节点依次入栈,直到遇到没有左子节点的节点。
- 访问节点:
- 弹出栈顶元素,该节点即为当前遍历到的最小节点。
- 计数器
k减一,表示已经访问了一个节点。- 检查是否找到第 k 小的元素:
- 如果计数器
k减到 0,说明当前节点即为第 k 小的元素,跳出循环。- 遍历右子树:
- 转向当前节点的右子树,重复步骤 2 和步骤 3,继续遍历。
- 返回结果:
- 当找到第 k 小的元素后,返回该节点的值。
199. 二叉树的右视图
通过深度优先搜索(DFS)的方式,利用递归函数进行遍历。
在递归过程中,使用一个列表来存储结果。
对于每个节点,判断当前结果列表的大小是否等于当前节点的深度,如果相等,说明该节点是其所在层从右向左第一个被访问到的节点,将其值加入结果列表。
为了优先处理每层的右边节点,先递归遍历右子树,再递归遍历左子树。最终返回存储右视图节点值的结果列表 。
114. 二叉树展开为链表
采用后序遍历的方式实现,具体步骤如下:
- 定义成员变量
head:
head用于保存展开后链表的头节点。- 递归函数
flatten:
- 如果当前节点
root为空,直接返回,不做任何处理。- 后序遍历:
- 先递归处理右子树
flatten(root.right)。- 再递归处理左子树
flatten(root.left)。- 处理当前节点:
- 将当前节点的左子树置为空
root.left = null,因为链表不需要左子树。- 将当前节点的右子树指向之前保存的
head,即展开后链表的头节点root.right = head。- 更新
head为当前节点head = root,这样在下一次递归处理左子树时,head始终指向已经展开的部分链表的头节点。通过这种方式,递归地将二叉树的每个节点都正确地连接到展开后的链表中,最终整棵树就被展开为一个链表。
105. 从前序与中序遍历序列构造二叉树(不熟悉,需着重复习)
- 定义全局参数:分别指向当前处理的前序遍历位置(preorder 数组)和当前处理的中序遍历位置(inorder 数组)
- 调用递归构建函数,使用一个“哨兵”值控制左右子树边界
- 辅助函数处理逻辑:
- 如果前序数组已经处理完,返回 null(递归终止条件)
- 如果当前中序元素等于哨兵值,说明当前子树构建结束,回溯。并移动中序指针,跳过当前哨兵
- 创建当前根节点(来自前序数组)
- 递归构建左子树:以当前节点值为界限
- 递归构建右子树:继续使用原哨兵(右边子树与当前节点平级)
437. 路径总和 III(不熟悉,需重点复习)
- 初始化哈希表:
- 使用一个
HashMap<Long, Integer>来存储前缀和及其出现的次数。- 初始化时,将前缀和
0的出现次数设为1,以处理从根节点开始的路径。- 递归遍历二叉树:
- 定义一个辅助函数
comp,用于递归计算符合条件的路径数量。- 在递归过程中,计算当前节点的前缀和
preSum,即从根节点到当前节点的路径和。- 计算符合条件的路径数量:
- 对于当前节点,检查哈希表中是否存在
preSum - targetSum的键。- 如果存在,说明从某个前驱节点到当前节点的路径和等于
targetSum,累加对应的值到count中。- 更新哈希表:
- 将当前的前缀和
preSum存入哈希表,并更新其出现次数。- 递归遍历左右子树:
- 分别递归处理左子节点和右子节点,累加它们的符合条件的路径数量到
count中。- 回溯:
- 在返回上一层递归之前,需要将当前节点的前缀和从哈希表中移除,防止影响其他路径的计算。
- 返回结果:
- 最终返回累加的
count,即所有符合条件的路径数量。
236. 二叉树的最近公共祖先
采用递归的方式进行求解,从根节点开始,对二叉树进行深度优先遍历。
对于每个节点,分别递归地在左子树和右子树中查找这两个指定节点。
如果在某个节点处,其左子树和右子树都找到了目标节点,那么这个节点就是最近公共祖先;
如果只在左子树中找到目标节点,那么最近公共祖先就在左子树中;
同理,如果只在右子树中找到目标节点,最近公共祖先就在右子树中;
如果左右子树都没有找到目标节点,则返回
null。
124. 二叉树中的最大路径和
| 概念 | 作用 | 实现方式 |
|---|---|---|
| DFS返回值 | 传递单边路径的最大贡献(局部最优解) | return node.val + max(left, right) |
| 全局最大值 | 记录整棵树的最大路径和(可能跨越子树) | 数组模拟引用传递 (int[] maxSum) |
| 递归过程 | 分而治之:分解为子树问题 + 合并全局结果 | 分治法(Divide and Conquer) |
该算法通过深度优先搜索(DFS)递归遍历二叉树。对于每个节点:
- 递归计算左右子树的最大路径贡献值,若为负数则舍弃(取
0)。- 计算当前节点的路径和(左贡献 + 节点值 + 右贡献),并更新全局最大值
maxSum。- 返回当前节点的单边最大路径和(节点值 + 左右贡献的较大者),供上层节点使用。
- 数组
maxSum用于在递归中维护全局最大值,避免使用全局变量。
图论
200. 岛屿数量
- 初始化变量:
res:用于记录岛屿的数量,初始值为0。- 遍历网格:
- 使用两层嵌套循环遍历整个网格,外层循环遍历行,内层循环遍历列。
- 发现陆地:
- 当遇到一个
'1'时,表示发现了一个新的岛屿,岛屿数量res加一。- 深度优先搜索(DFS):
- 调用
dfs函数,从当前陆地位置开始,递归地访问所有与之相连的陆地,并将这些陆地标记为已访问(例如标记为'2')。- DFS 函数实现:
- 如果当前位置超出网格边界,或者当前位置不是陆地(即不是
'1'),则返回。- 将当前位置标记为已访问(例如标记为
'2')。- 递归地访问当前位置的上、下、左、右四个方向的相邻位置。
- 返回结果:
- 遍历完所有网格后,返回岛屿数量
res。
994. 腐烂的橘子
- 初始化变量和队列:
- 获取网格的行数
m和列数n。- 使用队列
que存储腐烂橘子的位置。- 变量
freshCount记录当前新鲜橘子的数量。- 遍历网格,初始化队列和新鲜橘子计数:
- 遍历整个网格,遇到新鲜橘子则
freshCount++。- 遇到腐烂橘子则将其位置加入队列
que。- 特殊情况处理:
- 如果一开始没有新鲜橘子(
freshCount == 0),直接返回0分钟。- 广度优先搜索(BFS)遍历:
- 使用
round记录经过的分钟数。- 每一轮处理一层腐烂橘子,逐层遍历直到队列为空或没有新鲜橘子。
- 对于每一个腐烂橘子的位置,检查其上下左右四个方向:
- 确保不越界。
- 如果相邻单元格是新鲜橘子,则腐烂它,加入队列,并减少
freshCount。- 结果判断:
- BFS 结束后,如果
freshCount == 0,说明所有橘子都已腐烂,返回round。- 否则,返回
-1,表示有新鲜橘子无法被腐烂。
207. 课程表(拓扑排序,着重复习)
- 初始化数据结构:
- 使用邻接表
edges来表示课程之间的依赖关系。- 使用数组
in来记录每个课程的入度(即有多少课程依赖于它)。- 构建邻接表和入度数组:
- 遍历
prerequisites数组,对于每一个依赖关系[a, b]:
- 在邻接表中将
a添加到b的依赖列表中,表示b依赖于a。- 增加课程
a的入度。- 初始化队列:
- 将所有入度为
0的课程加入队列,表示这些课程没有前置课程,可以立即学习。- 拓扑排序:
- 当队列不为空时,取出队首的课程
v,表示完成该课程。- 增加已完成课程计数
count。- 遍历课程
v所依赖的所有课程x,减少它们的入度。- 如果某个课程
x的入度变为0,将其加入队列,表示现在可以学习该课程。- 结果判断:
- 最后,比较完成的课程数
count是否等于总课程数numCourses。- 如果相等,说明所有课程都可以完成,返回
true;否则,返回false。
208. 实现 Trie (前缀树)
- Trie结构定义:
- 定义一个
Trie类,包含一个根节点root。Node内部类表示Trie中的每个节点,包含一个长度为26的Node数组son(对应26个字母)和一个布尔值isEnd表示是否为一个单词的结束。- 构造函数:
- 初始化Trie,创建一个空的根节点。
- 插入操作:
- 从根节点开始,遍历要插入的单词的每个字符。
- 对于每个字符,计算其在
son数组中的索引,并检查对应的子节点是否存在。- 如果不存在,则创建一个新的节点。
- 移动到下一个节点,直到单词的所有字符都插入完毕。
- 最后一个节点的
isEnd标记设置为true,表示这是一个完整的单词。- 搜索操作:
- 调用辅助方法
find来检查单词是否存在于Trie中。- 如果
find返回1,表示单词存在;否则,不存在。- 前缀搜索操作:
- 调用辅助方法
find来检查是否有单词以给定前缀开始。- 如果
find返回的不是-1,表示有单词以该前缀开始;否则,不存在。- 辅助查找方法:
- 从根节点开始,遍历单词或前缀的每个字符。
- 对于每个字符,检查对应的子节点是否存在。
- 如果不存在,返回-1表示单词或前缀不存在。
- 如果遍历完所有字符,节点不为null,表示单词或前缀存在。
- 根据
isEnd的值返回1(完整单词)或0(前缀)。
回溯
解题技巧
上来先排序,问题少一半。
修剪无关枝,复杂少一半。
回溯框架用,难度少一半。
循环组合用,重复也不怕。
46. 全排列
- 初始化结果列表和当前路径列表:
res用于存储所有排列的结果。list用于存储当前正在构建的排列路径。- 调用回溯函数:
- 从空路径开始,调用
backtrack函数生成所有排列。- 回溯函数
backtrack:
- 终止条件:当
list的长度等于nums的长度时,说明已经生成了一个完整的排列,将其加入结果列表res并返回。- 选择路径:遍历
nums中的每一个元素,如果该元素不在当前路径list中,则将其加入路径。- 递归探索:调用
backtrack函数继续探索下一个元素。- 撤销选择:在递归返回后,从路径中移除最后一个元素,回退到上一步,尝试其他可能的元素。
78. 子集
- 初始化数据结构:
element:用于存储当前正在构建的子集。ans:用于存储所有生成的子集。- 定义回溯函数
backtracking:
- 参数:
nums:输入的整数数组。startIndex:当前回溯的起始索引,决定从数组的哪个位置开始选择元素。- 终止条件:
- 如果
startIndex大于或等于数组长度,说明已经遍历完所有元素,终止递归。- 递归过程:
- 从
startIndex开始,遍历数组中的每个元素。- 将当前元素添加到
element中,表示选择该元素。- 将当前的
element(作为一个新的子集)添加到ans中。这里使用new ArrayList<>(element)确保ans中存储的是独立的子集,避免后续修改影响已存储的子集。- 递归调用
backtracking,从下一个索引i + 1开始,继续选择下一个元素。- 回溯阶段:移除刚刚添加的元素,尝试不选择当前元素的其他可能组合。
- 主函数
subsets的流程:
- 首先,将空集
[]添加到结果列表ans中,因为空集是所有集合的子集。- 调用
backtracking函数,从索引0开始生成所有可能的子集。- 最后,返回包含所有子集的
ans列表。
17. 电话号码的字母组合
初始化数据结构:
map数组存储每个数字对应的字母集合。sb是一个StringBuilder,用于动态构建当前的字母组合路径。res列表用于存储所有生成的字母组合。主函数逻辑:
- 检查输入是否为空或长度为0,如果是,则直接返回空的
res列表。- 调用
backtrack函数开始生成字母组合。回溯函数逻辑:
终止条件: 当
sb的长度等于输入数字字符串的长度时,说明已经生成了一个完整的字母组合,将其添加到res中,并返回。递归过程:
- 根据当前索引
index获取对应的字母字符串。- 遍历该字母字符串中的每一个字母:
- 将当前字母添加到
sb中。- 递归调用
backtrack处理下一个数字(index + 1)。- 回溯:移除刚刚添加的字母,尝试下一个可能的字母。
生成所有组合:
- 通过递归和回溯,算法会遍历所有可能的字母组合,并将它们添加到结果集
res中。
39. 组合总和
- 初始化数据结构:
- 创建一个列表
res用于存储最终的结果。- 调用
backtrack函数开始进行回溯搜索。- 回溯函数逻辑:
- 终止条件: 当
target等于 0 时,说明当前组合的和正好为目标值,将当前组合加入结果集res中。- 遍历候选数组:从当前索引
index开始遍历候选数组candidates
- 剪枝优化: 如果当前候选数
candidates[i]大于剩余的目标值target,则无需继续考虑该数及其后面的数,直接跳过。- 选择当前数: 将当前候选数
candidates[i]加入到当前组合list中。- 递归调用: 继续递归搜索,更新剩余目标值为
target - candidates[i],并且索引仍为i(因为一个数可以被重复使用)。- 回溯撤销: 递归返回后,移除最后一个添加到
list中的数,以便尝试其他可能的组合。
22. 括号生成
- 初始化结果列表和调用回溯函数:
- 创建一个
List<String>类型的结果列表res来存储所有有效的括号组合。- 调用
backtrack函数开始生成括号组合,初始时传入一个空的StringBuilder对象,以及左右括号的使用数量均为0,总的括号对数为n。- 回溯函数的终止条件:
- 当已使用的右括号数量
closeNum等于总的括号对数max时,说明已经生成了一个有效的括号组合。- 将当前的括号组合
current.toString()添加到结果列表res中,并返回。- 添加左括号的条件和操作:
- 如果已使用的左括号数量
openNum小于总的括号对数max,可以继续添加左括号。- 向
current中添加一个左括号'('。- 递归调用
backtrack函数,更新左括号的使用数量为openNum + 1,其他参数不变。- 回溯操作:移除刚刚添加的左括号,以便尝试其他可能的组合。
- 添加右括号的条件和操作:
- 如果已使用的右括号数量
closeNum小于已使用的左括号数量openNum,可以继续添加右括号。- 向
current中添加一个右括号')'。- 递归调用
backtrack函数,更新右括号的使用数量为closeNum + 1,其他参数不变。- 回溯操作:移除刚刚添加的右括号,以便尝试其他可能的组合。
79. 单词搜索
- 初始化数据结构:
- 定义一个二维数组
directions表示四个可能的移动方向(上、下、左、右)。- 获取网格的行数
rowLen和列数colLen。- 初步检查:
- 如果网格的总单元格数小于单词的长度,直接返回
false,因为不可能匹配整个单词。- 遍历网格:
- 使用双重循环遍历网格中的每一个单元格,尝试从每个位置开始搜索单词。
- 回溯搜索:
- 终止条件:当
index等于单词长度时,说明已经成功匹配整个单词,返回true。- 剪枝条件:
- 检查当前坐标是否越界。
- 检查当前单元格的字符是否与单词的当前字符匹配。
- 标记访问:将当前单元格临时标记为已访问(例如,用
'#'替换),防止在本次路径中重复使用。- 递归搜索:尝试向四个方向进行深度优先搜索,如果任意方向返回
true,则整个函数返回true。- 回溯恢复:如果四个方向都未找到匹配,恢复当前单元格的原始值,以便其他路径可以重新访问该单元格。
- 返回结果:
- 如果遍历完所有可能的起始点后仍未找到匹配的单词,返回
false。
131. 分割回文串
采用回溯算法来枚举所有可能的分割方案。对于字符串的每一个位置,尝试将其作为分割点,判断分割出的子串是否为回文串。如果是,则将该子串加入当前的分割方案,并递归处理剩余部分。如果不是,则继续尝试下一个分割点。当处理到字符串末尾时,将当前的分割方案加入结果集。
- 初始化数据结构:
- 使用
List<List<String>> res存储所有有效的分割方案。- 使用
List<String> list来构建当前的分割方案。- 主函数
partition的逻辑:
- 调用回溯函数
backtrack,从字符串的起始位置开始递归处理。- 回溯函数
backtrack的逻辑:
- 终止条件: 当当前索引
index等于字符串长度时,表示已经遍历完整个字符串,将当前的分割方案list加入结果集res。- 遍历所有可能的分割点: 从当前索引
index开始,遍历到字符串末尾,尝试将s.substring(index, i + 1)作为分割出的子串。- 判断回文:使用辅助函数
isPal判断子串是否为回文串。
- 如果是回文串,将其加入当前的分割方案
list,并递归处理剩余部分s.substring(i + 1)。- 递归返回后,进行回溯,将刚刚加入的子串从
list中移除,尝试下一个可能的分割点。- 辅助函数
isPal的逻辑:
- 使用双指针法,从字符串的两端向中间遍历,比较对应位置的字符是否相等。
- 如果所有对应字符都相等,则返回
true,否则返回false。
51. N 皇后
- 初始化:
- 创建结果列表
res。- 初始化
queens数组,用于记录每行皇后的列位置。- 生成模板字符串列表
templates,每个模板表示棋盘的一行,其中'Q'表示皇后位置,'.'表示空位。- 深度优先搜索(DFS):
- 从第
0行开始递归尝试放置皇后。- 对于每一行,计算所有可用的列位置,通过位运算排除已被占用的列和对角线。
- 遍历所有可用列,选择一个列放置皇后,并递归到下一行,同时更新占用的列和对角线掩码。
- 如果当前行数等于
n,将当前的queens数组转换为棋盘表示并添加到结果列表res中。- 回溯时,移除当前选择的列,继续尝试其他可能的列。
- 构建解决方案:
- 当找到一个有效解时,遍历
queens数组,根据每个皇后的列位置从templates获取对应的行字符串,构建完整的棋盘表示,并添加到结果列表中。- 返回结果:
- 完成所有可能的搜索后,返回包含所有有效解决方案的列表
res。
二分查找
35. 搜索插入位置
二分查找经典用法
74. 搜索二维矩阵
解题思路:
采用二分查找算法,分两步进行:
- 在矩阵的第一列中进行二分查找,确定目标值可能在哪一行。
- 在确定的行中进行二分查找,判断目标值是否存在。
题解:
- 初始化数据结构:
- 定义
searchMatrix方法作为主函数,接收二维矩阵matrix和目标值target。- 确定可能包含目标值的行:
- 调用
binarySearchFirst方法,在矩阵的第一列中进行二分查找,找到可能包含目标值的行索引rowIndex。- 如果
rowIndex小于 0,说明目标值小于矩阵的最小值,直接返回false。- 在确定的行中进行二分查找:
- 调用
binarySearch方法,在确定的行matrix[rowIndex]中进行二分查找,判断目标值是否存在。- 如果找到目标值,返回
true;否则,返回false。- 二分查找第一列的方法
binarySearchFirst:
- 初始化
up为 0,down为矩阵的行数减一。- 使用二分查找确定目标值可能在哪一行:
- 计算中间行索引
mid。- 如果
matrix[mid][0]小于等于目标值,说明目标值可能在mid行或更下面的行,更新res为mid,并继续在下半部分查找。- 否则,目标值在
mid行的上面,更新down为mid - 1。- 返回
res,即可能包含目标值的行索引。- 二分查找行的方法
binarySearch:
- 初始化
left为 0,right为行的长度减一。- 使用二分查找在行中查找目标值:
- 计算中间索引
mid。- 如果
nums[mid]等于目标值,返回true。- 如果
nums[mid]大于目标值,更新right为mid - 1。- 否则,更新
left为mid + 1。- 如果未找到目标值,返回
false。
34. 在排序数组中查找元素的第一个和最后一个位置
利用二分
binarySearch查找元素位置
- 查找目标值的起始位置:
- 查找第一个大于等于目标值的位置
start。- 验证目标值是否存在:
- 如果
start超出数组范围或nums[start]不等于目标值,说明目标值不存在,返回[-1, -1]。- 查找目标值的结束位置:
- 使用
binarySearch查找第一个大于target的位置,然后减1得到目标值的结束位置end。- 返回结果:
- 返回包含起始位置
start和结束位置end的数组。
33. 搜索旋转排序数组
二分查找 + 判断有序区间
判断有序区间:
- 如果左半部分
[left, mid]是有序的:
- 如果目标值在
[left, mid)之间,调整右边界到mid - 1。- 否则,调整左边界到
mid + 1。- 否则,右半部分
[mid + 1, right]是有序的:
- 如果目标值在
(mid, right]之间,调整左边界到mid + 1。- 否则,调整右边界到
mid - 1。
153. 寻找旋转排序数组中的最小值
- 初始化二分查找的左右边界:
left初始化为数组的起始位置0。right初始化为数组的末尾位置nums.length - 1。- 进行二分查找:
- 当
left小于right时,继续查找。- 计算中间位置
mid,使用left + (right - left) / 2来防止整数溢出。- 判断中间元素与右边元素的关系:
- 如果
nums[mid] < nums[right],说明最小值在左半部分(包括中间元素),将right缩小到mid。- 否则,最小值在右半部分(不包括中间元素),将
left缩小到mid + 1。- 找到最小值:
- 当
left等于right时,说明已经找到最小值的位置,返回nums[left]。
4. 寻找两个正序数组的中位数
- 总体思路:
- 将寻找两个数组的中位数问题转化为寻找第
k小的元素的问题。- 通过比较两个数组中的元素,逐步缩小搜索范围,直到找到所需的第
k小的元素。- 具体步骤:
- 步骤1: 计算两个数组的总长度
sum = m + n。- **步骤2:**根据
sum的奇偶性,确定中位数的位置:
- 如果
sum为奇数,中位数为第(sum / 2 + 1)大的元素。- 如果
sum为偶数,中位数为第(sum / 2)和第(sum / 2 + 1)大的元素的平均值。- **步骤3:**实现
findKSmall方法,用于在两个数组中寻找第k小的元素:
- 边界条件处理:
- 如果其中一个数组已经遍历完,则直接在另一个数组中找第
k小的元素。- 如果
k == 1,则返回两个数组当前起始位置的最小值。- 递归查找:
- 计算在两个数组中可以取的步长
k/2,选择较小步长的元素进行比较。- 比较两个数组在步长位置的元素,排除较小的部分,调整
k的值,继续在剩余部分查找。
栈
20. 有效的括号
遇到左括号压入栈,遇到右括号从栈中取出。若两个括号不匹配,则无效。
判断完毕之后,根据栈是否还有元素判断是否有效。
155. 最小栈
解法1:使用单链表实现
- 初始化栈:
- 创建一个虚拟头节点
head,其val可以是任意值,min初始化为Integer.MAX_VALUE,表示当前最小值。- 推入元素 (
push):
- 每次推入新元素时,创建一个新的节点,其
val为新元素的值。- 新节点的
min为当前新元素值和前一个节点的min中的较小者。- 将新节点链接到链表的头部,更新
head指向新节点。- 弹出元素 (
pop):
- 将
head指向下一个节点,丢弃当前头节点。- 获取栈顶元素 (
top):
- 返回
head.val,即当前头节点的值。- 获取最小值 (
getMin):
- 返回
head.min,即从当前头节点到栈底的最小值。
解法2:使用双栈实现
- 初始化栈:
- 创建两个栈:
xStack:用于存储所有推入栈的元素。minStack:用于存储当前的最小值。初始化时推入Integer.MAX_VALUE。- 推入元素 (
push):
- 将新元素
x推入xStack。- 将
x和minStack栈顶元素中的较小者推入minStack,以保持minStack的栈顶始终为当前最小值。- 弹出元素 (
pop):
- 同时从
xStack和minStack弹出栈顶元素,确保两个栈的同步。- 获取栈顶元素 (
top):
- 返回
xStack的栈顶元素。- 获取最小值 (
getMin):
- 返回
minStack的栈顶元素,即当前栈中的最小值。
394. 字符串解码
解题思路:
使用栈来解决这个问题。遍历字符串,当遇到数字时,解析完整的数字作为重复次数;当遇到左括号时,将当前的重复次数和字符串片段分别压入对应的栈中,并重置它们;当遇到右括号时,从栈中弹出重复次数和之前的字符串片段,将当前的字符串片段重复相应的次数后,追加到之前的字符串片段后面。题解:
- 初始化数据结构:
- 使用两个栈,一个用于存储字符串片段 (
strStack),一个用于存储重复次数 (numStack)。- 遍历字符串:
- 对于每一个字符,判断它是数字、左括号、右括号还是普通字符。
- 处理数字字符:
- 如果当前字符是数字,更新当前的重复次数
times。考虑到多位数字,使用times = times * 10 + (c - '0')来累积数字。- 处理左括号 ‘[’:
- 将当前的重复次数
times压入numStack。- 将当前的字符串片段
res压入strStack。- 重置
times为 0,重置res为一个新的StringBuilder,准备构建括号内的字符串。- 处理右括号 ‘]’:
- 弹出
strStack的栈顶字符串片段temp,这是需要重复的部分。- 弹出
numStack的栈顶重复次数curTimes。- 将
temp重复curTimes次,并追加到新的res中。- 处理普通字符:
- 直接将字符追加到当前的字符串片段
res中。- 返回结果:
- 遍历完整个字符串后,
res即为解码后的字符串,返回res.toString()。
739. 每日温度
解题思路:
使用单调栈来解决这个问题。单调栈是一种特殊的栈,它保持栈内元素的单调性。在这个问题中,我们将保持栈内元素对应的温度是递减的。题解:
- 初始化数据结构:
- 获取温度数组的长度
length。- 初始化结果数组
res,长度与温度数组相同,初始值默认为0。- 使用双端队列
Deque作为栈stack来存储温度数组的索引。- 遍历温度数组:
- 对于每一天的温度
currentTemperature,检查栈是否非空且当前温度是否高于栈顶索引对应的温度。- 更新结果数组:
- 如果当前温度高于栈顶索引对应的温度,则弹出栈顶索引
previousIndex,并计算当前索引i与previousIndex的差值,更新结果数组res[previousIndex]。- 维护单调栈:
- 将当前索引入栈,继续遍历下一天的温度。
- 返回结果数组:
- 遍历结束后,返回结果数组
res。
84. 柱状图中最大的矩形
- 初始化辅助数组和栈:
left和right数组分别存储每个柱子左右两边第一个小于当前柱子的索引。right数组初始化为length,表示最后一个柱子右边没有柱子。- 使用双端队列
stack存储柱子索引。- 遍历每个柱子:
- 当栈不为空且当前柱子高度小于等于栈顶柱子高度时,更新栈顶柱子的
right索引。- 更新当前柱子的
left索引。- 将当前柱子索引入栈。
- 计算最大矩形面积:
- 遍历每个柱子,计算以该柱子为高度的最大矩形面积,更新结果。
堆
215. 数组中的第K个最大元素
- 调整 k 值:
- 将 k 转换为数组长度减去 k,以适应快速选择算法的查找第 k 小元素的需求。
- 初始化左右指针和基准值:
- 设置左右指针
i和j,以及基准值p。- 分区操作:
- 使用
do-while循环从左右两端向中间移动指针,找到需要交换的元素,并进行交换。- 递归查找:
- 根据 k 的位置决定递归的方向,继续在左半部分或右半部分查找。
347. 前 K 个高频元素
- 找最小最大值:
- 初始化
max和min为数组的第一个元素。- 遍历数组,更新
max和min。- 构造频率数组:
- 创建一个频率数组
freqs,长度为max - min + 1。- 遍历输入数组,统计每个数字出现的频率,存储在
freqs中。- 获取最高频率:
- 初始化
maxFreq为0。- 遍历频率数组
freqs,找到最高频率maxFreq。- 构造结果数组:
- 创建一个结果数组
res,长度为k。- 从
maxFreq开始,逐次递减,找到频率等于当前最大频率的数字,并将其加入结果数组res。- 重复上述过程,直到找到
k个高频元素或频率降为0。
295. 数据流的中位数
解题思路:
使用两个堆来实现:
- 一个大根堆(
maxHeap)存储较小的一半元素。- 一个小根堆(
minHeap)存储较大的一半元素。通过维护两个堆的大小平衡,确保大根堆的大小始终比小根堆大0或1,从而快速找到中位数。
题解:
- 初始化:
- 创建一个大根堆
maxHeap和一个小根堆minHeap。- 使用自定义比较器实现大根堆和小根堆。
- 添加元素 (
addNum):
- 如果
maxHeap为空或者当前元素小于maxHeap的堆顶元素,将元素添加到maxHeap。- 否则,将元素添加到
minHeap。- 平衡两个堆的大小:
- 如果
maxHeap比minHeap大2,将maxHeap的堆顶元素移到minHeap。- 如果
minHeap比maxHeap大1,将minHeap的堆顶元素移到maxHeap。- 查找中位数 (
findMedian):
- 如果两个堆的大小相等,中位数是两个堆顶元素的平均值。
- 否则,中位数是
maxHeap的堆顶元素。
贪心算法
121. 买卖股票的最佳时机
- 初始化变量:
profit用于记录当前找到的最大利润,初始值为0。min用于记录到目前为止的最低买入价格,初始值为第一天的股票价格。- 遍历价格数组:
- 对于每一天的股票价格,首先检查是否需要更新最低买入价格
min。- 然后计算如果当天卖出股票能获得的利润,并更新
profit为当前最大利润和计算利润中的较大值。- 返回结果:
- 遍历结束后,
profit即为所能获得的最大利润,直接返回。
55. 跳跃游戏
- 初始化数组长度
n和最远可达位置rightmost。- 遍历数组中的每个元素:
- 如果当前位置超出最远可达位置,返回
false。- 更新最远可达位置。
- 如果最远可达位置已覆盖或超过最后一个位置,返回
true。- 遍历结束后,若未提前返回
true,则返回false。
45. 跳跃游戏 II
- 初始化变量:
length记录数组长度。mostRight记录当前能到达的最远位置。endPos记录当前跳跃的边界位置。steps记录跳跃次数。- 遍历数组:
- 从第一个元素遍历到倒数第二个元素。
- 更新
mostRight为当前位置能到达的最远位置。- 判断跳跃:
- 如果当前位置到达了
endPos,则更新endPos为mostRight,并增加跳跃次数steps。- 返回结果:
- 返回跳跃次数
steps。
763. 划分字母区间
- 记录每个字符最后出现的位置:
- 初始化一个长度为26的数组
last。- 遍历字符串
s,更新last数组中每个字符的最后出现位置。- 确定每个部分的起始和结束位置:
- 初始化两个指针
start和end。- 再次遍历字符串
s,更新end为当前字符最后出现的位置和之前记录的end的较大值。- 当遍历到
end位置时,划分一个部分,记录其长度,并更新start为下一个部分的起始位置。- 返回结果列表:
- 返回包含每个部分长度的结果列表。
动态规划
70. 爬楼梯
解题思路:
这道题可以通过动态规划来解决。我们可以定义一个数组dp,其中dp[i]表示爬到第i个台阶的方法数。状态转移方程为:
d**p[i]=d**p[i−1]+d**p[i−2]
即爬到第i个台阶的方法数等于爬到第i-1个台阶的方法数加上爬到第i-2个台阶的方法数。题解:
- 初始化变量:
p表示前前一个台阶的方法数,初始为 0。q表示前一个台阶的方法数,初始为 0。r表示当前台阶的方法数,初始为 1(因为爬到第 1 个台阶只有一种方法)。- 遍历每个台阶:
- 从第 1 个台阶遍历到第
n个台阶。- 在每次迭代中,更新
p和q的值,使其分别表示前一个台阶和当前台阶的方法数。- 计算当前台阶的方法数
r,即p + q。- 返回结果:
- 遍历结束后,
r即为爬到第n个台阶的方法数。
118. 杨辉三角
- 初始化结果列表:创建一个
List<List<Integer>>类型的变量res来存储最终的杨辉三角结果。- 遍历每一行:使用一个外层循环,从第0行到第
numRows-1行,逐行生成杨辉三角的每一行。- 初始化当前行列表:对于每一行,创建一个
List<Integer>类型的变量list来存储当前行的元素。- 遍历当前行的每一个元素:使用一个内层循环,从第0个到第
i个,逐个生成当前行的元素。
- 处理边界情况:如果当前元素是行的第一个或最后一个元素(即
j == 0或j == i),则该元素的值为1。- 计算中间元素:否则,当前元素的值等于上一行相邻两个元素的和,即
res.get(i - 1).get(j - 1) + res.get(i - 1).get(j)。- 添加当前行到结果列表:将生成的当前行
list添加到结果列表res中。- 返回结果:循环结束后,返回生成的杨辉三角结果
res。
198. 打家劫舍
- 处理边界条件:
- 如果数组为空或长度为0,返回0。
- 如果数组长度为1,返回唯一的房屋金额。
- 初始化动态规划数组:
dp[0]设为nums[0]。dp[1]设为nums[0]和nums[1]中的较大值。- 状态转移:
- 从第2个房屋开始遍历,计算每个位置的最大偷窃金额,取偷窃当前房屋和不偷窃当前房屋的较大值。
- 返回结果:
- 返回
dp数组的最后一个值,即最大偷窃金额。
279. 完全平方数
- 初始化动态规划数组:
- 创建一个大小为
n+1的数组dp,其中dp[i]表示组成数字i所需的最少完全平方数的数量。- 初始化时,
dp[0]默认为0,因为组成数字0不需要任何完全平方数。- 遍历每个数字:
- 对于每个数字
i从1到n,初始化min为Integer.MAX_VALUE,用于记录组成i的最小完全平方数数量。- 尝试所有可能的完全平方数:
- 对于每个
i,遍历所有可能的完全平方数j*j,其中j*j <= i。- 更新
min为f[i - j*j]和当前min中的较小值,表示在使用了j*j后,剩下的部分所需的最小完全平方数数量。- 更新动态规划数组:
- 将
dp[i]设置为min + 1,因为使用了当前的完全平方数j*j,所以数量加一。- 返回结果:
- 最后返回
dp[n],即组成数字n所需的最少完全平方数的数量。
322. 零钱兑换
- 初始化变量和数组:
- 定义
max为amount + 1,作为初始的"无穷大"值,表示无法凑出对应金额。- 创建一个大小为
max的数组dp,其中dp[i]表示凑出金额i所需的最少硬币数。- 使用
Arrays.fill将dp数组的所有元素初始化为max,表示初始状态下所有金额都无法凑出。- 设置
dp[0] = 0,因为凑出金额0不需要任何硬币。- 排序硬币数组:
- 对硬币数组
coins进行排序,以便在后续遍历过程中可以提前终止不必要的循环(当硬币面值大于当前金额时)。- 动态规划填充dp数组:
- 外层循环遍历从
1到amount的所有金额i。- 内层循环遍历所有的硬币面值
coins[j]:
- 如果当前硬币面值
coins[j]大于当前金额i,则无需继续遍历更大的硬币,使用break提前终止内层循环。- 否则,更新
dp[i]为当前值dp[i]和使用当前硬币后的值dp[i - coins[j]] + 1中的较小者。这里dp[i - coins[j]] + 1表示使用当前硬币后,凑出剩余金额所需的硬币数加上当前这枚硬币。- 返回结果:
- 最后检查
dp[amount]的值:
- 如果
dp[amount]仍然等于max,说明无法凑出目标金额amount,返回-1。- 否则,返回
dp[amount],即凑出目标金额所需的最少硬币数。
139. 单词拆分
解题思路:
使用动态规划的方法来解决这个问题。定义一个布尔数组dp,其中dp[i]表示字符串s的前i个字符是否可以被拆分为wordDict中的单词。题解:
- 初始化:
- 获取字符串
s的长度,并加 1 作为dp数组的长度。- 初始化
dp[0]为true,表示空字符串可以被拆分。- 动态规划:
- 遍历字符串
s的每一个位置i,从 1 到s.length()。- 对于每一个位置
i,遍历字符串s的每一个位置j,从 0 到i。- 如果
dp[j]为true,表示s的前j个字符可以被拆分,并且s.substring(j, i)在wordDict中,表示s的第j到第i个字符是一个单词。- 那么
s的前i个字符也可以被拆分,设置dp[i]为true,并跳出内层循环。- 返回结果:
- 返回
dp[s.length()],表示整个字符串s是否可以被拆分为wordDict中的单词。
300. 最长递增子序列
采用动态规划结合二分查找的方法,时间复杂度为 O(n log n)。
- 维护一个
dp数组,其中dp[i]表示长度为i+1的递增子序列的末尾元素的最小值。- 遍历数组
nums中的每个元素num,使用二分查找在dp数组中找到num应该插入的位置position。- 如果
position为负数,表示num不在dp中,通过-position - 1计算出插入位置。然后将dp[position]更新为num。- 如果
position等于当前的maxLength,说明找到了一个更长的递增子序列,maxLength自增。最终,
maxLength就是最长递增子序列的长度。
152. 乘积最大子数组
- 初始化变量:
maxF、minF和res初始值为数组的第一个元素nums[0]。- 遍历数组:
- 从第二个元素开始,保存当前的
maxF和minF。- 更新
maxF和minF,考虑当前元素本身、乘以之前的最大乘积、乘以之前的最小乘积。- 更新全局最大乘积
res。- 返回结果:
- 遍历结束后,返回全局最大乘积
res。
416. 分割等和子集
- 计算总和:
- 遍历数组,计算数组的总和
sum。- 检查奇偶性:
- 如果总和
sum是奇数,返回false。- 目标和:
- 计算目标和
target为sum / 2。- 动态规划初始化:
- 初始化布尔数组
dp,dp[0]设为true。- 动态规划遍历:
- 遍历数组中的每个元素
nums[i],从后向前更新dp数组。- 返回结果:
- 返回
dp[target],表示是否可以找到一个子集,使得其和为target。
32. 最长有效括号
解题思路:
使用动态规划的方法来解决这个问题。定义一个数组dp,其中dp[i]表示以第i个字符结尾的最长有效括号子串的长度。题解:
- 初始化变量和数组:
- 初始化
res为 0,用于记录最长有效括号子串的长度。- 创建一个数组
dp,长度与输入字符串s相同,用于记录以每个字符结尾的最长有效括号子串的长度。- 遍历字符串:
- 从第二个字符开始遍历字符串中的每个字符。
- 如果当前字符是
')',则进行以下判断:
- 情况一: 如果前一个字符是
'(',说明当前字符和前一个字符组成了一对有效括号。此时更新dp[i]为前两个字符的最长有效括号子串长度加上当前这对括号的长度(2)。如果i >= 2,还需要加上前面的有效括号子串长度。- 情况二: 如果前一个字符是
')',需要检查是否可以与当前字符组成有效括号子串。具体是检查i - dp[i - 1] - 1位置的字符是否为'('。如果是,则更新dp[i]为前面的有效括号子串长度加上当前这对括号的长度(2),并且如果前面还有有效括号子串,还需要加上前面的长度。- 更新
res为当前dp[i]和res中的较大值。- 返回结果:
- 遍历结束后,
res即为最长有效括号子串的长度,返回res。
多维动态规划
62. 不同路径
- 初始化一维动态规划数组:
- 创建一个长度为
col的一维数组dp,其中dp[j]表示到达当前行第j列的路径数。- 初始化所有元素为
1,因为在第一行和第一列,机器人只有一种路径到达每个位置(一直向右或一直向下)。- 遍历网格中的每一个位置:
- 从第二行开始,逐行遍历网格。
- 对于每一行,从第二列开始,逐列遍历。
- 对于每个位置
(i, j),其路径数等于上方位置(i-1, j)和左方位置(i, j-1)的路径数之和。- 由于使用一维数组优化空间复杂度,上方位置的值对应于
dp[j](上一行的同一列),左方位置的值对应于dp[j - 1](同一行的前一列)。- 更新
dp[j] += dp[j - 1],即累加左方和上方的路径数。- 返回结果:
- 遍历完成后,
dp[col - 1]即为到达右下角位置(row-1, col-1)的总路径数。
64. 最小路径和
解题思路:
使用动态规划算法来解决这个问题。定义一个二维数组dp,其中dp[i][j]表示从左上角到达网格位置(i, j)的最小路径和。通过填充这个dp数组,最终得到右下角位置的最小路径和。题解:
- 检查输入有效性:
- 如果输入的网格为空或没有元素,直接返回 0。
- 初始化变量:
- 获取网格的行数
rows和列数columns。- 创建一个与输入网格大小相同的二维数组
dp,用于存储到达每个位置的最小路径和。- 初始化起点:
- 起点位置
(0, 0)的最小路径和就是该位置的值grid[0][0]。- 初始化第一列:
- 对于第一列的每个位置
(i, 0),只能从上方位置(i-1, 0)到达,因此dp[i][0] = dp[i-1][0] + grid[i][0]。- 初始化第一行:
- 对于第一行的每个位置
(0, j),只能从左方位置(0, j-1)到达,因此dp[0][j] = dp[0][j-1] + grid[0][j]。- 填充剩余网格位置:
- 对于其他位置
(i, j),可以从上方(i-1, j)或左方(i, j-1)到达,因此dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + grid[i][j]。- 返回结果:
- 最终,右下角位置
(rows-1, columns-1)的最小路径和即为所求结果。
5. 最长回文子串
该算法采用中心扩展法来寻找最长回文子串。
- 遍历字符串中的每个字符
- 对于每个字符,分别以该字符为中心(考虑奇数长度回文)以及该字符和下一个字符为中心(考虑偶数长度回文)
- 通过
getLen方法向两边扩展来计算回文子串的长度。getLen方法不断向两边扩展,直到无法构成回文为止,然后返回当前找到的回文子串长度。- 在主方法中,记录下每次找到的最长回文子串的长度以及对应的左右边界索引,最后根据这些索引截取并返回最长回文子串 。
1143. 最长公共子序列
解题思路:
使用动态规划算法来解决这个问题。定义一个二维数组dp,其中dp[i][j]表示text1的前i个字符和text2的前j个字符的最长公共子序列长度。题解:
- 初始化变量:
- 获取两个字符串的长度,并加1作为
dp数组的维度,方便处理边界情况。- 创建二维数组
dp:
dp[i][j]表示text1的前i个字符和text2的前j个字符的最长公共子序列长度。- 遍历字符串:
- 遍历
text1的每个字符,获取当前字符c1。- 遍历
text2的每个字符,获取当前字符c2。- 状态转移:
- 如果当前字符相等,则最长公共子序列长度加1,即
dp[i][j] = dp[i-1][j-1] + 1。- 如果当前字符不相等,则取
text1前i-1个字符和text2前j个字符的最长公共子序列长度,和text1前i个字符和text2前j-1个字符的最长公共子序列长度中的较大值,即dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1])。- 返回结果:
- 返回
text1和text2的最长公共子序列长度,即dp[t1Max-1][t2Max-1]。
72. 编辑距离
- 初始化变量和dp数组:
- 获取
word1和word2的长度,并加1作为dp数组的行数和列数,以包含空字符串的情况。- 创建一个二维数组
dp[w1Max][w2Max],用于存储转换所需的最少操作数。- 初始化dp数组的第一行和第一列:
- 第一列表示将
word1的前i个字符转换成空字符串所需的操作数,即删除i个字符,所以dp[i][0] = i。- 第一行表示将空字符串转换成
word2的前j个字符所需的操作数,即插入j个字符,所以dp[0][j] = j。- 填充dp数组:
- 从第二行第二列开始遍历,对于每个
dp[i][j]:
- 如果
word1[i-1] == word2[j-1],则不需要操作,dp[i][j] = dp[i-1][j-1]。- 如果字符不相等,则考虑三种操作(插入、删除、替换)中的最小值,并加1:
dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1。- 返回结果:
- 最终,
dp[w1Max-1][w2Max-1]即为将word1转换成word2所需的最少操作数。
技巧
136. 只出现一次的数字
利用异或运算的性质:
- 任何数和 0 做异或运算,结果仍然是原来的数,即
a ^ 0 = a。- 任何数和其自身做异或运算,结果是 0,即
a ^ a = 0。- 异或运算满足交换律和结合律,即
a ^ b ^ a = (a ^ a) ^ b = 0 ^ b = b。因此,数组中所有出现两次的元素通过异或运算后会相互抵消,最终剩下的结果就是只出现一次的元素。
169. 多数元素
同归于尽消杀法:
由于多数超过50%, 比如100个数,那么多数至少51个,剩下少数是49个。
- 第一个到来的士兵,直接插上自己阵营的旗帜占领这块高地,此时领主 winner 就是这个阵营的人,现存兵力 count = 1。
- 如果新来的士兵和前一个士兵是同一阵营,则集合起来占领高地,领主不变,winner 依然是当前这个士兵所属阵营,现存兵力 count++;
- 如果新来到的士兵不是同一阵营,则前方阵营派一个士兵和它同归于尽。 此时前方阵营兵力count --。(即使双方都死光,这块高地的旗帜 winner 依然不变,因为已经没有活着的士兵可以去换上自己的新旗帜)
- 当下一个士兵到来,发现前方阵营已经没有兵力,新士兵就成了领主,winner 变成这个士兵所属阵营的旗帜,现存兵力 count ++。
就这样各路军阀一直以这种以一敌一同归于尽的方式厮杀下去,直到少数阵营都死光,那么最后剩下的几个必然属于多数阵营,winner 就是多数阵营。(多数阵营 51个,少数阵营只有49个,死剩下的2个就是多数阵营的人)
75. 颜色分类
解题思路:
使用三指针法进行排序,将数组分为三个部分:0的部分、1的部分和2的部分。通过遍历数组,将0交换到左边,2交换到右边,中间自然为1的部分。题解:
- 初始化指针:
left指针用于放置0,初始化为0。right指针用于放置2,初始化为数组的最后一个元素。- 遍历数组:
- 使用
i指针遍历数组,从左到右。- 如果当前元素是2且已经在最右边,则无需处理,直接返回。
- 当当前元素是2时,将其与
right指针位置的元素交换,并将right指针左移。- 如果当前元素是0,将其与
left指针位置的元素交换,并将left指针右移。- 交换函数:
- 定义一个辅助函数
swap,用于交换数组中两个元素的位置。
31. 下一个排列
- 从数组的末尾开始向前遍历,寻找第一个出现降序的位置(即当前数字大于前一个数字的位置)。
- 将该位置后面的子数组进行升序排序,以确保这部分子数组中最小的数位于最前面。
- 在排序后的子数组中找到刚好大于前一个数字的最小值,并与前一个数字进行交换。这样就得到了一个刚好大于当前排列的下一个排列。
- 如果整个数组都是降序的,说明当前排列已经是最大的排列,此时只需将整个数组进行升序排序,得到最小的排列作为下一个排列。
287. 寻找重复数
解题思路:
本题可以使用 Floyd’s Tortoise and Hare (Cycle Detection) 算法来解决。这个算法通常用于检测链表中的环,但在这里可以巧妙地应用到数组中,因为数组中的每个元素都可以看作是指向下一个节点的指针。题解:
- 初始化指针:
- 初始化两个指针
slow和fast,都指向数组的第一个元素。- 寻找相遇点:
- 使用
do-while循环,slow指针每次移动一步,fast指针每次移动两步。- 当
slow和fast相遇时,说明数组中存在一个环。- 寻找环的入口:
- 将
slow指针重新指向数组的第一个元素。- 使用
while循环,slow和fast指针每次都移动一步,直到它们再次相遇。- 相遇点即为重复的数字。
- 返回结果:
- 返回
slow指针的值,即为重复的数字。