连续的定义
维基百科给出的定义:
连续函数(英语:Continuous function)是指函数在数学上的属性为连续。直观上来说,连续的函数就是当输入值的变化足够小的时候,输出的变化也会随之足够小的函数。
- 所以不要直观地认为,一个函数看起来没有很突变的拐点就一定连续,这种理解是不对的。
严格的定义是:对于任意的 ϵ > 0 \epsilon >0 ϵ>0 ,存在 δ > 0 \delta>0 δ>0 当 ∣ x − x 0 ∣ < δ |x-x_0|<\delta ∣x−x0∣<δ,有 ∣ f ( x ) − f ( x 0 ) ∣ < ϵ |f(x)-f(x_0)|<\epsilon ∣f(x)−f(x0)∣<ϵ 那么这个函数就是连续的。
- 这可以看做是一种彼此之间的对抗,A 说:对于函数 f ( x ) f(x) f(x) 在 x 0 x_0 x0 处的取值,我给出一个很小的数 ϵ \epsilon ϵ, f ( x 0 ) f(x_0) f(x0) 及其附近很近的点都得在这个 ϵ \epsilon ϵ 划定的窄带内 [ f ( x 0 ) − ϵ , f ( x 0 ) + ϵ ] [f(x_0)-\epsilon, f(x_0)+\epsilon] [f(x0)−ϵ,f(x0)+ϵ] 我才判定你这个函数在 x 0 x_0 x0 附近是没有突变的。
- B 说:行吧,我给你找一个同样很小的数 δ \delta δ 我能够证明 [ x 0 − δ , x 0 + δ ] [x_0-\delta, x_0+\delta] [x0−δ,x0+δ] 范围内所有的数,他们的 f ( x ) f(x) f(x) 都在你划定的窄带 ϵ \epsilon ϵ 范围之内。
- A 说:行,你只要找到这个 δ \delta δ 我就认可你。
关于 ϵ \epsilon ϵ 和 δ \delta δ 的解释
- 这两个都是非常小的值,但是一旦选定某个 ϵ \epsilon ϵ 之后,你可以认为他是个定值,那么你的任务就是针对这个定值选一个合适的 δ \delta δ 来证明你的函数确实是连续的
- 比如我现在有个函数 f ( x ) = x 2 f(x)=x^2 f(x)=x2 我要证明在 x = 0 x=0 x=0 这一点连续,首先假设我选了个 ϵ = 0.1 \epsilon=0.1 ϵ=0.1 那么现在 [ f ( x ) − ϵ , f ( x ) + ϵ ] [f(x)-\epsilon, f(x)+\epsilon] [f(x)−ϵ,f(x)+ϵ] 就是窄带的的范围,就是 [ − 0.1 , 0.1 ] [-0.1, 0.1] [−0.1,0.1]。所以你接下来选的 x 0 x_0 x0 值都落在 [ x − δ , x + δ ] [x-\delta, x+\delta] [x−δ,x+δ] 之间,并用这些 x 0 x_0 x0 对应的 f ( x 0 ) f(x_0) f(x0) 来证明这些 f ( x 0 ) f(x_0) f(x0) 全部落在 ϵ \epsilon ϵ 划定的窄带中 ,现在如果我选了 δ = 0.05 \delta=0.05 δ=0.05 那么当 x 0 ∈ [ − 0.05 , 0.05 ] x_0\in [-0.05, 0.05] x0∈[−0.05,0.05] 对应的 f ( x 0 ) f(x_0) f(x0) 的取值范围是 [ 0 , 0.0025 ] [0, 0.0025] [0,0.0025] 而这个范围也确实小于 ϵ \epsilon ϵ 所划定的 [ − 0.1 , 0.1 ] [-0.1, 0.1] [−0.1,0.1] 的窄带内
- 所以以上例子至少证明了 f ( x ) f(x) f(x) 这个函数在 ϵ = 0.1 \epsilon=0.1 ϵ=0.1, δ = 0.05 \delta=0.05 δ=0.05 的情况下是连续的
- 这里只是给出一个直观的例子来看,为什么要用 ϵ , δ \epsilon, \delta ϵ,δ 这么一组值来判定函数的连续性
不连续的函数范例
-
f
(
x
)
=
s
i
n
(
1
x
)
f(x)=sin(\frac{1}{x})
f(x)=sin(x1) 这个函数就是不连续的,如果我们将它在 0-1 的范围内的图画出来,是这个样子:
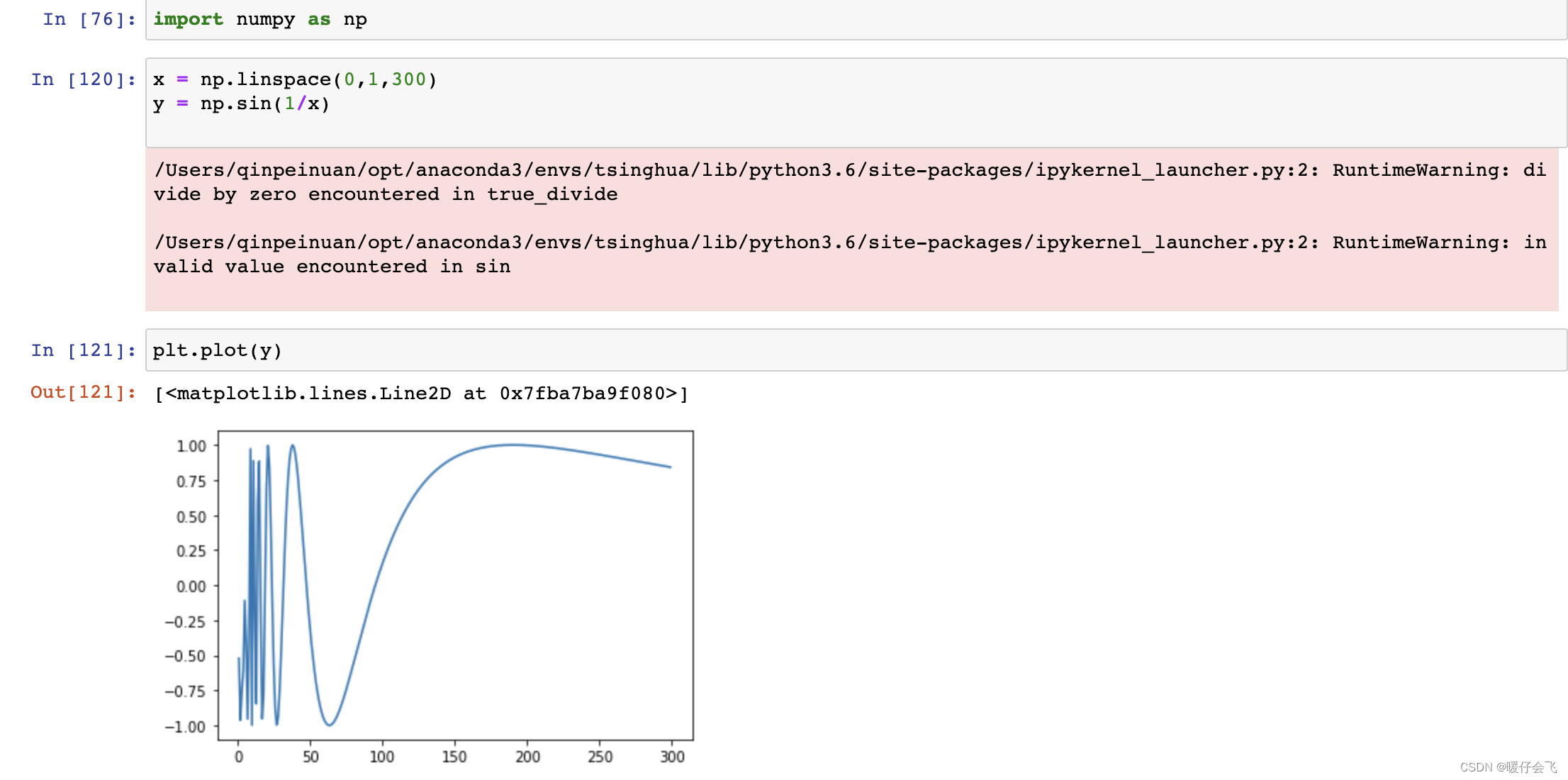
- 再进一步,如果我们画出它在
x
=
[
0
,
0.1
]
x=[0,0.1]
x=[0,0.1] 范围内的图:
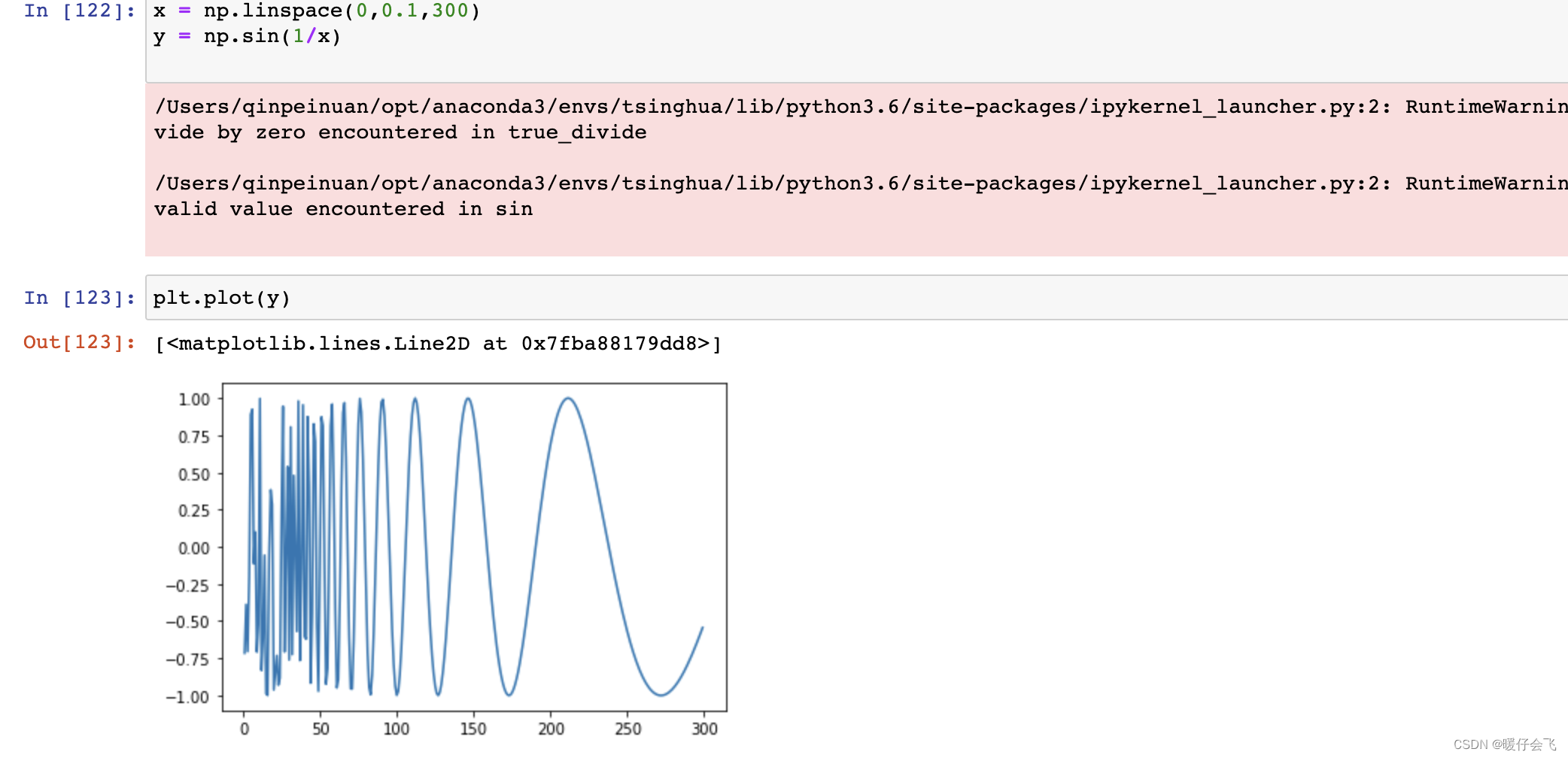
- 再进一步
x
=
[
0
,
0.0001
]
x=[0,0.0001]
x=[0,0.0001] 范围内的图
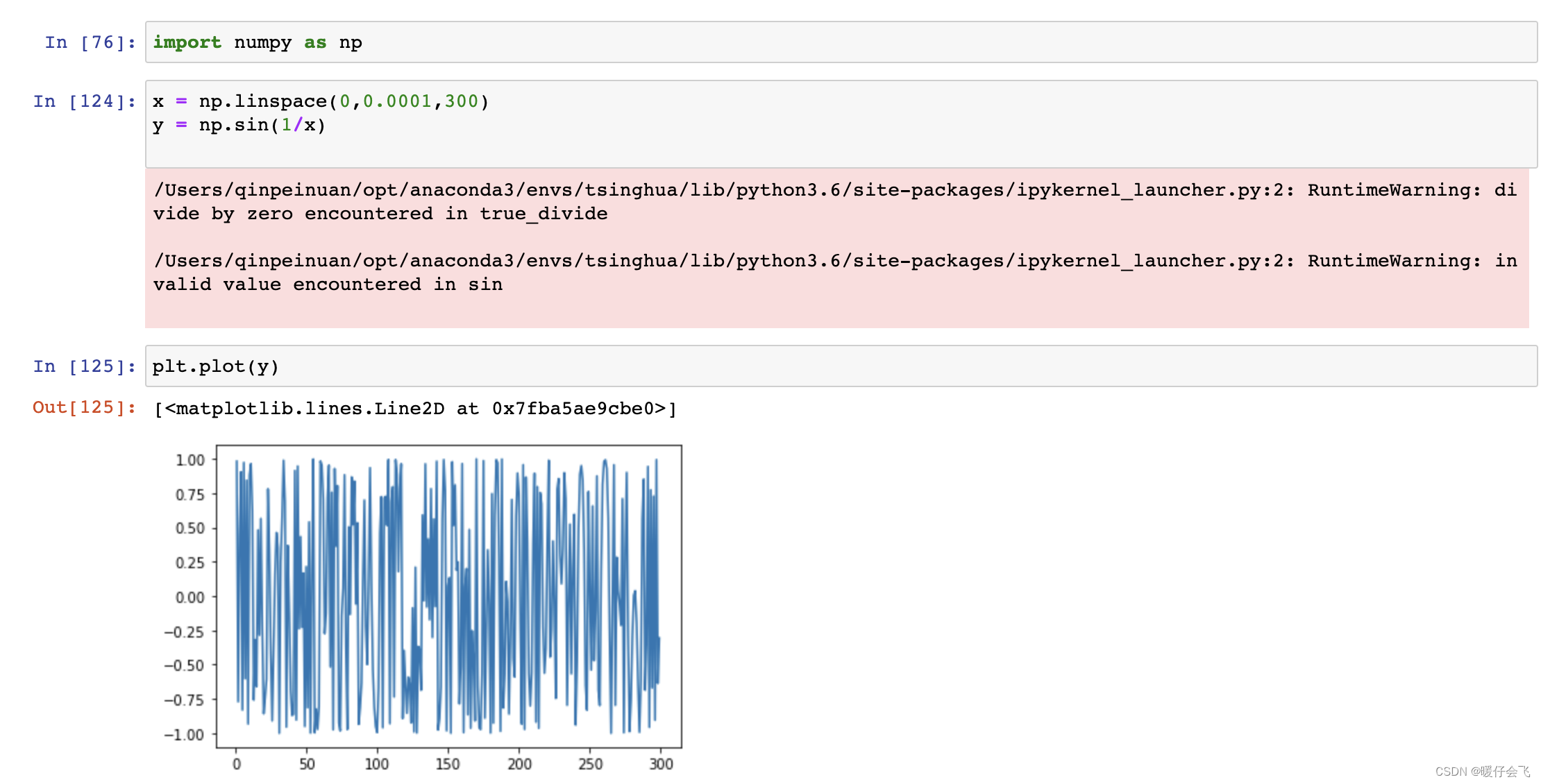
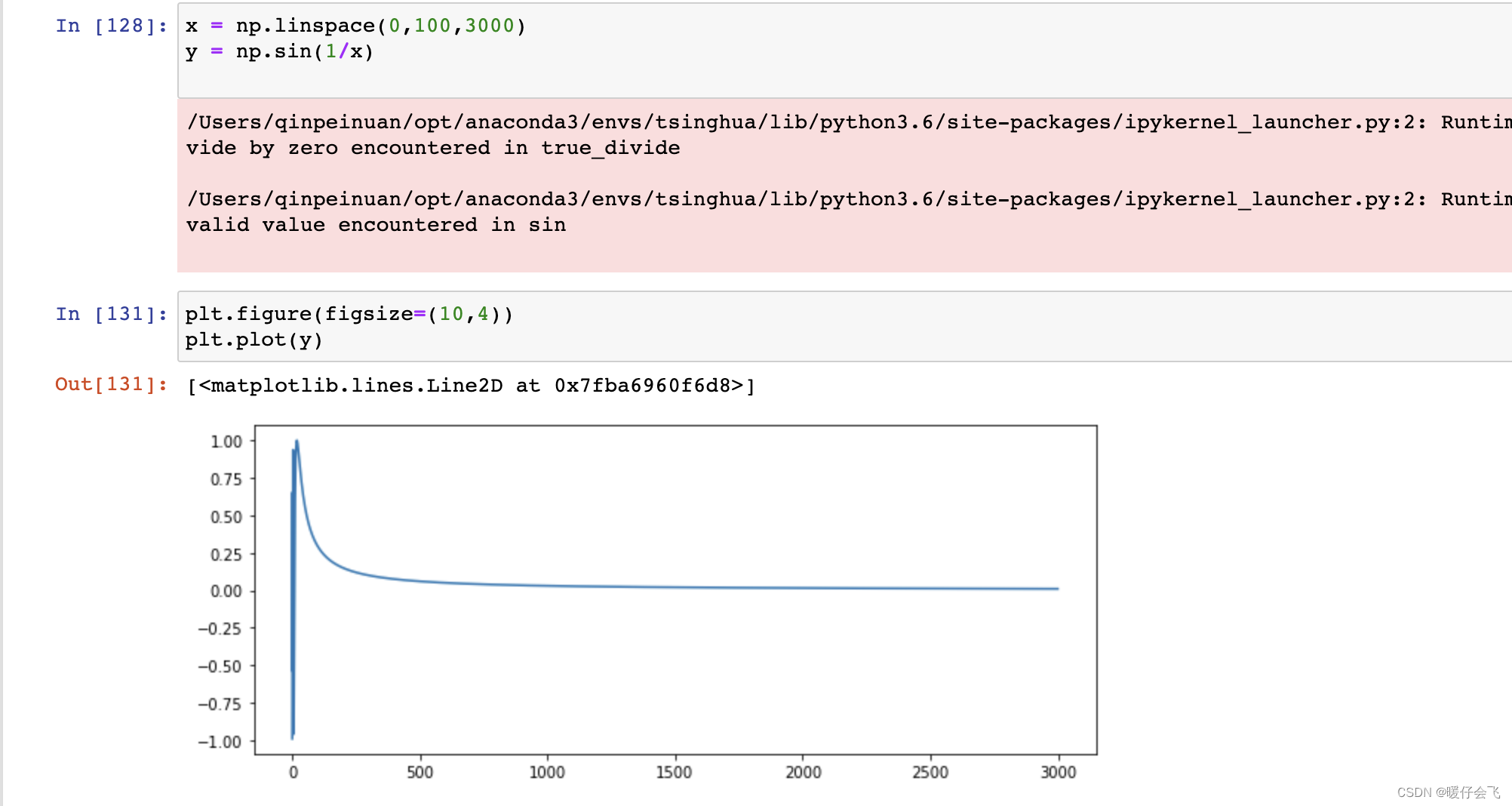
- 你会发现,无论你的 δ \delta δ 取多小,他的 x x x 对应的值都会在这个范围内剧烈震荡,也就是说没有任何一个 δ \delta δ 能保证这个 f ( x ) f(x) f(x) 收敛到 [ f ( x ) − ϵ , f ( x ) + ϵ ] [f(x)-\epsilon, f(x)+\epsilon] [f(x)−ϵ,f(x)+ϵ]
- 究其原因是 s i n sin sin 中包含一个 1 x \frac{1}{x} x1 而这个 1 x \frac{1}{x} x1 在越趋近于 0 0 0 的位置震动值越大,而且增速越快,这就表示着外面嵌套一个 s i n sin sin 之后,就越靠近零整个 f ( x ) f(x) f(x) 的值震荡幅度就越大越密集。所以他永远不可能收敛到一个点,因此这个函数在 x = 0 x=0 x=0 附近是不连续的。
- 但是他在
0
0
0 之后的表现都是连续的

![[附源码]java毕业设计网上学车预约系统](https://img-blog.csdnimg.cn/e971b900604d4fad8949e154583d708e.png)








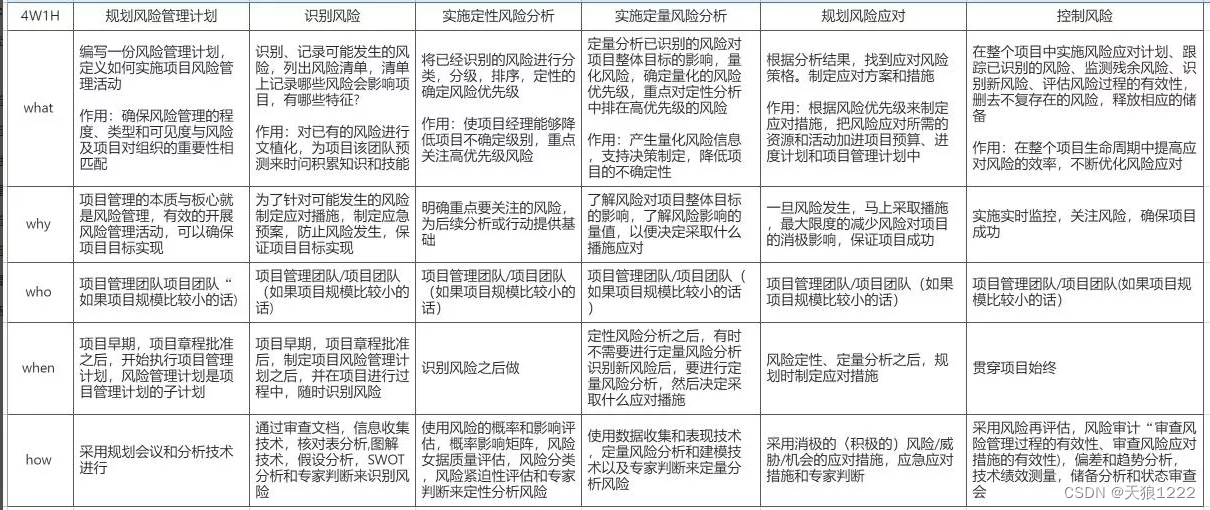

![[附源码]java毕业设计文章管理系统查重PPT](https://img-blog.csdnimg.cn/5d775b6c9e2942d98ddaeab3c186831d.png)

![[附源码]java毕业设计小区物业管理系统论文](https://img-blog.csdnimg.cn/eb647dea0ed842edbf9db194c44bdb75.png)