回顾其他数据结构（每种数据结构都有自己特定的应用场景）：

• 数组：通过下标查询很快，插入和删除数据的时候，效率会很低，需要大量元素的位移。
• 链表：插入和删除效率很高，查找效率低，需要从头开始依次访问链表中每个数据项，直到找到
• 哈希表：插入、删除、查询效率都很高，但是空间利用率不高，抵触使用的是数组，某些单元没有被利于到。

树结构

树（Tree）是n(n>0)个节点的有限集，n=0，称为空树

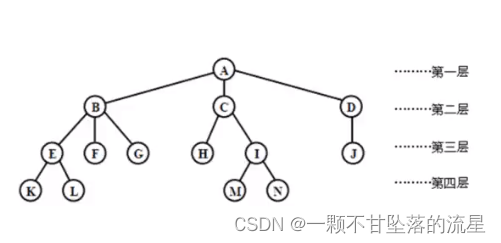
• 从逻辑上看，树具有以下特定：

1. 任何非空树中有且仅有一个节点是没有前驱节点的，这个节点就是根节点
2. 除根节点之外，其余的节点有且仅有一个与之相连的前驱节点
3. 包括根节点在内，每个节点可以有多个直接相连的后继节点
4. 树形结构是一种具有递归特性的数据结构（任何一颗树又满足树的概念）
5. 树形结构种的数据元素之间存在的关系是：一对多、或者多对一的关系

• 树的术语：

1. 节点的度: 节点所拥有子树的个数
2. 树的度: 树中节点度的最大值，如上图中：树的度为3
3. 叶子节点: 度为0的节点，如上图中：K、L、F、G、H、M、N、J都是
4. 分支节点: 度不为0的节点（除根节点之外的分支节点统称为：内部节点。根节点又称之为：开始节点）
5. 子节点: 节点的直接后驱。    
6. 父节点: 节点的直接前驱。  
7. 兄弟节点: 具有同一父节点的个节点彼此就是兄弟节点。
8. 路径: 这个节点自上而下的通过每条节点上的每条边
9. 路径长度: 路径所包含的边的个数。
10. 节点层次: 规定根节点的层是 1，其余节点的层数等于父节点的层数加1.
11. 树的深度: 树中所有节点层数的最大值。

树的存储结构：计算机只能是顺序或者是链式的存储，所以树这样的结构是不能够直接存储的，要将其转换为顺序或者链式存储

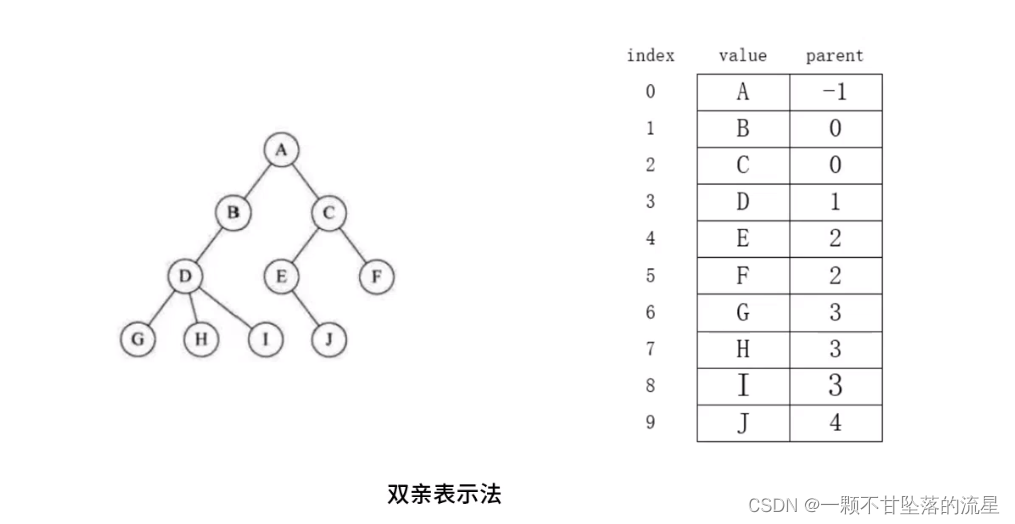
1. 双亲表示法： 双亲表示法采用数组存储普通的树。
   其核心思想：顺序存储每个节点的同时，给各节点附加一个记录其父节点位置的变量，存储的父节点的下标。
   实际操作的时候，就是从上往下，顺序遍历一棵树，并为相应的域赋值。
   优点：可以快速的获取任意节点的父节点位置。
   缺点：如果要获取某个节点的子节点，就得遍历

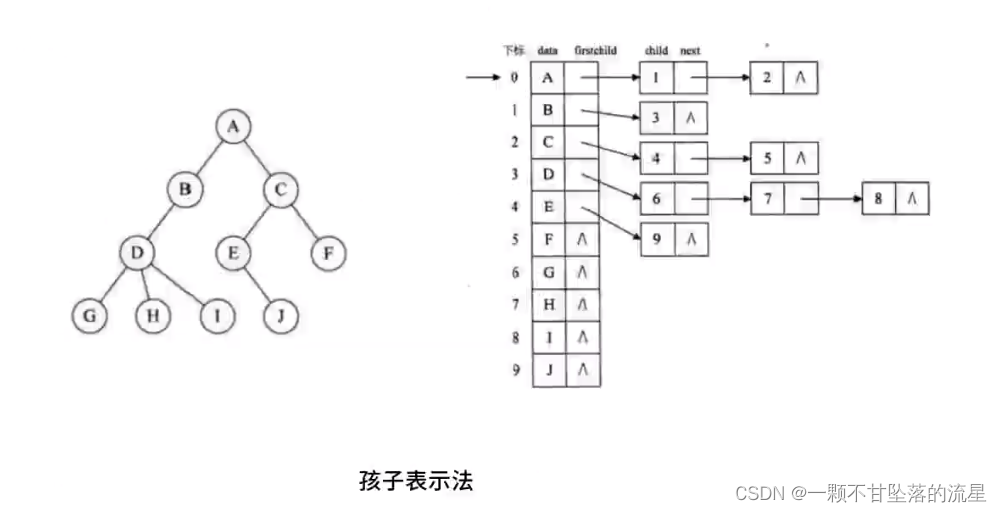
2. 孩子表示法：建立多个指针域，指向它的子节点的地址。
   也就是说，任何一个节点，都掌握它所有的子节点的信息。通过数组+链表的形式来实现。
   顺序表=>数组，从树的根节点开始，使用数组依次存储树的各个节点。
   需要注意的是：它会给各个节点配备一个链表，用于存储各个节点的孩子节点位于数组中的位置。
   如果说，节点没有子节点，则该节点的链表为空链表。

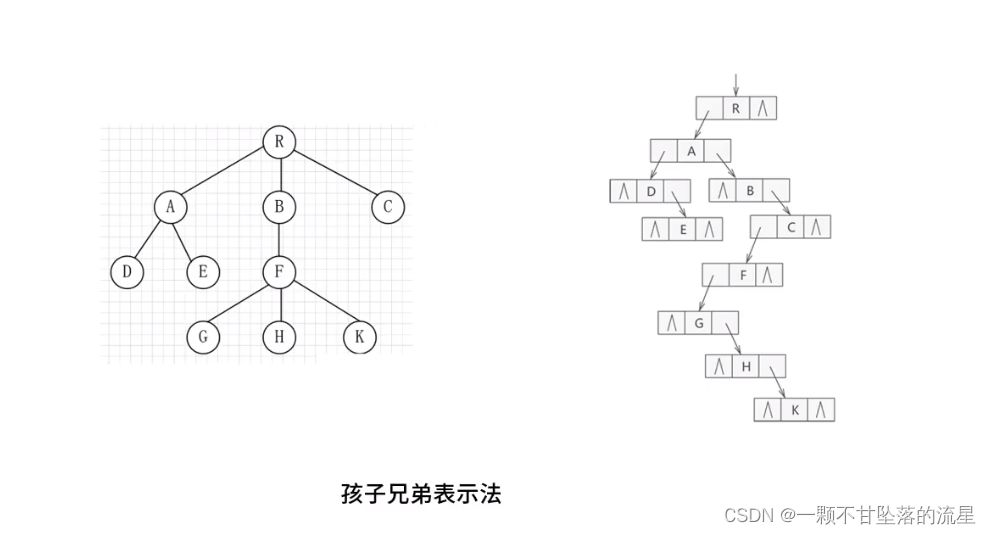
3. 孩子兄弟表示法：把普通的树，转成二叉树：从树的根节点开始，依次用链表存储各个节点的孩子节点和兄弟节点。

二叉树

其实所有树的本质都是可以通过二叉树进行模拟出来。

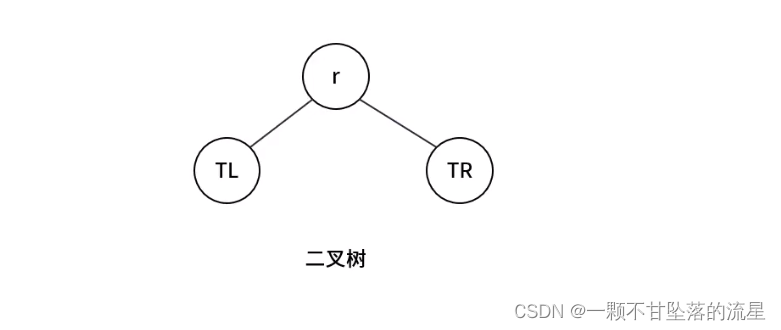
• 如果树中每个节点最多只能有2个子节点，这样的树我们称之为二叉树。
• 二叉树可以为空，也就是没有节点，空二叉树。
• 若不为空，则它是由根节点和称为其左子树TL和右子树TR的两个不相交的二叉树组成。

二叉树特点：

1. 每个节点最多有2颗子树，不存在度大于2的节点
2. 左子树和右子树是有序的，次序不能任意颠倒
3. 即使树中某个节点只有一颗子树，也要区分他是左子树还是右子树。

二叉树性质：

1. 在二叉树中，第 i 层是最多有 2^i-1 次节点（i>=1）。第一层就是：2^1-1 = 1
2. 在二叉树中，如果深度为 k，那么最多有 2^k-1 个节点

二叉树形态：

1. 空树
2. 只有一个根节点
3. 只有一个左子节点
4. 只有一个右子节点
5. 两个子节点都有

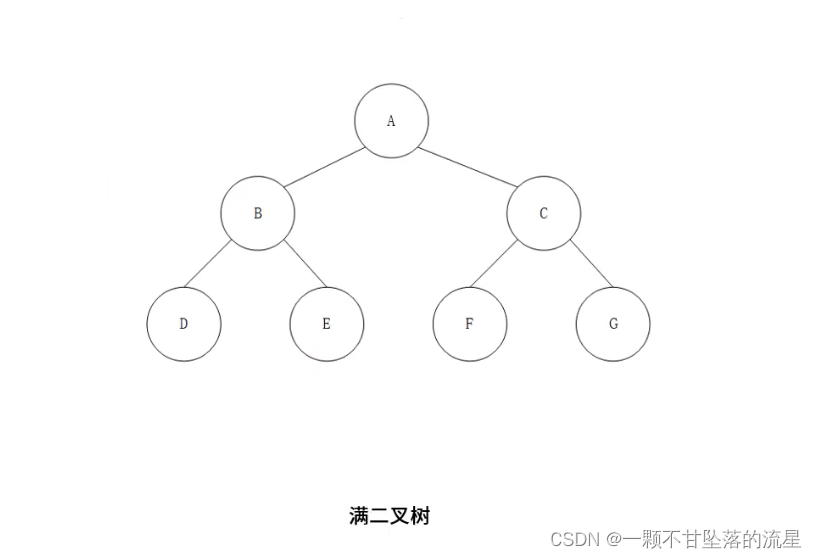
• 满二叉树：在一颗二叉树中，如果所有的分支节点度存在左子树和右子树，并且所有的叶子都在同一层上，这样的二叉树就是满二叉树。
• 满二叉树叶子只能出现最下一层，出现在其他层，不可能达成平衡，非叶子节点的度一定是2.
• 满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。
  
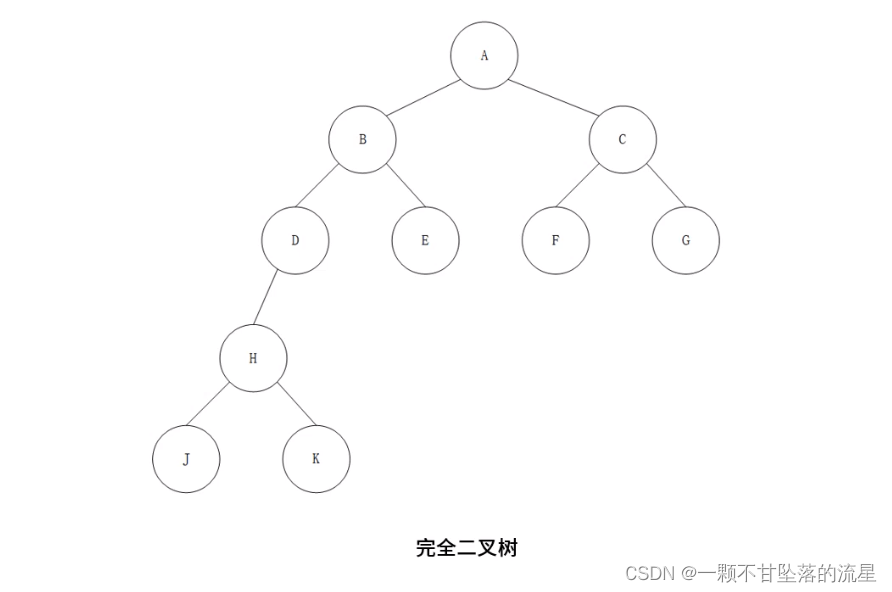
• 完全二叉树：除最后一层外，每一层的节点数均达到最大值，最后一层指缺失右边的若干节点。
• 把右边缺失的节点补齐，那它就是一个满二叉树。
  
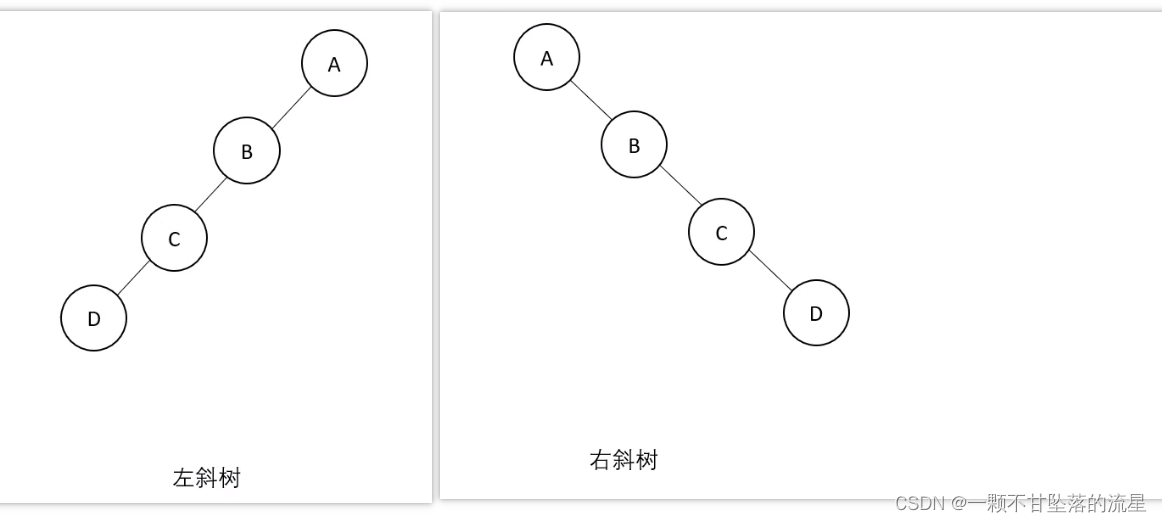
• 斜树：所有的节点都只有左子树或右子树

二叉搜索树

二叉搜索树（BST：binary search tree），又称二叉查找树、二叉排序树

二叉树对节点是没有任何限制的，而二叉搜索树其实就是普通的二叉树上加了一些限制：

1. 非空左子树的所有的键值都 小于 其根节点的键值
2. 非空右子树的所有的键值都 大于 其根节点的键值
3. 左右子树本身也都是二叉树

二叉搜索树的遍历指：不重复的访问二叉树中所有的节点

先序遍历：1. 访问根节点 2. 先序遍历其左子树 3. 先序遍历其右子树
中序遍历：先递归遍历其左子树，从最后一个左子树开始存入数组，然后回溯遍历双亲结点，再是右子树同理。
后序遍历：1. 后序遍历其左子树 2. 后序遍历其右子树 3. 访问根节点

• js 实现一个简单的二叉搜索树

// 节点
class Node {
	constructor(value) {
		this.value = value;
		this.left = null;
		this.right = null;
	}
}

// 二叉搜索树
class BinarySearchTree {
	constructor() {
		// 根节点
		this.root = null;
	}
	// 插入值
	insert(value) {
		let newNode = new Node(value);
		// 如果是空树，这个就是根节点
		if(this.root === null){
			this.root = newNode;
		}else{
			this.insertNode(this.root,newNode);
		}
	}
	// 插入值的比较
	insertNode(node, newNode){
		// 右边：大值
		if(newNode.value > node.value){
			if(node.right === null){
				node.right = newNode;
			}else {
				this.insertNode(node.right, newNode);
			}
		}else if(newNode.value < node.value){ // 左边：小值
			if(node.left === null){
				node.left = newNode;
			}else{
				this.insertNode(node.left,newNode);
			}
		}
	}
	// 先序遍历
	preOrderTraversal(cb) {
		this.preOrederTraversalNode(this.root,cb);
	}
	preOrederTraversalNode(node,cb){
		// 空节点直接返回
		if(node === null) return;
		// 打印
		cb(node.value);
		// 遍历所有的左子树
		this.preOrederTraversalNode(node.left,cb);
		// 遍历所有的右子树
		this.preOrederTraversalNode(node.right,cb);
	}
	// 中序遍历
	inOrderTraversal(cb) {
		this.inOrderTraversalNode(this.root,cb);
	}
	inOrderTraversalNode(node,cb){
		if(node === null) return;
		this.inOrderTraversalNode(node.left,cb);
		cb(node.value);
		this.inOrderTraversalNode(node.right,cb);
	}
	// 后序遍历
	postOrderTraversal(cb) {
		this.postOrderTraversalNode(this.root,cb);
	}
	postOrderTraversalNode(node,cb){
		if(node === null) return;
		this.postOrderTraversalNode(node.left,cb);
		this.postOrderTraversalNode(node.right,cb);
		cb(node.value);
	}
	// 最小值
	min(){
		let node = this.root;
		// 找到左边的节点就是最小的值
		while(node.left !== null){
			node = node.left;
		}
		return node.value;
	}
	// 最大值
	max(){
		let node = this.root;
		// 找到左边的节点就是最小的值
		while(node.right !== null){
			node = node.right;
		}
		return node.value;
	}
	// 寻找特定值
	search(val){
		// 获取根节点
		let node = this.root;
		// 通过判断node节点的值和传入val大小
		while(node!==null){
			if(node.value > val){
				node = node.left;
			}else if(node.value < val){
				node = node.right;
			}else {
				return true;
			}
		}
	}
}

const bst = new BinarySearchTree();
bst.insert(11);
bst.insert(7);
bst.insert(15);
bst.insert(5);
bst.insert(3);
bst.insert(9);
// 二叉搜索树结构
console.log(bst);
// 先序遍历
const preArr = [];
const preCb = (val)=>{
	preArr.push(val);
}
bst.preOrderTraversal(preCb);
console.log(preArr);
// 中序遍历
const inArr = [];
const inCb = (val)=>{
	inArr.push(val);
}
bst.inOrderTraversal(inCb);
console.log(inArr);
// 后序遍历
const postArr = [];
const postCb = (val)=>{
	postArr.push(val);
}
bst.postOrderTraversal(postCb);
console.log(postArr);
// 最值
console.log(bst.min());
console.log(bst.max());
// 寻找特定值
console.log(bst.search(9));

• 运行结果：

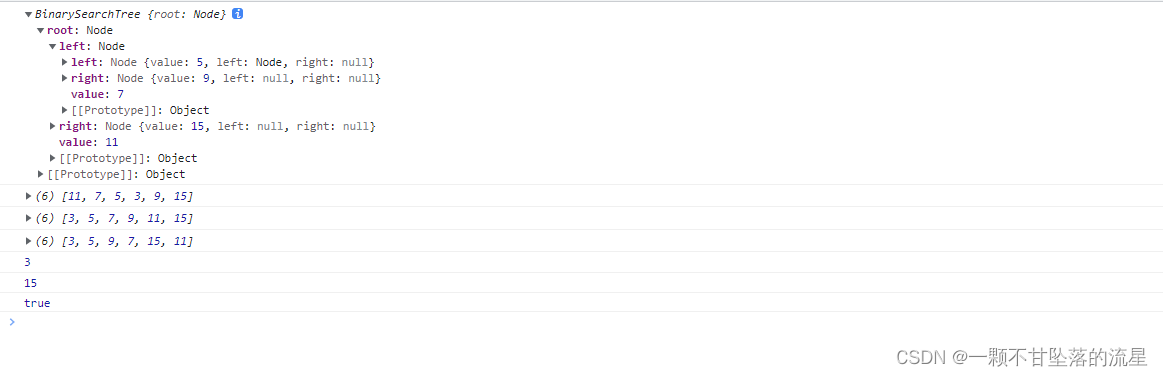
二叉搜索树的优点：可以快速的找到给定的关键字的数据项，并且可以快速的插入和删除
二叉搜索树的缺点：具有局限性，同样的数据，可以对应不同的二叉搜索树、
比较好的二叉搜索树的结构：左右分布均匀，但是我们插入连续的数据的时候，会导致数据分布不均匀、
我们把这种分布不均匀的树称之为：非平衡树

平衡树（AVL树）

为了能以较快的时间O(logN)来操作一棵树，我们需要保证树总是平衡的

• 至少大部分是平衡的，那么时间复杂度也是接近O(logN)的
• 也就是说树中每个节点左边的子孙节点的个数，应该尽可能的等于每个节点右边的子孙节点的个数。
• AVL树是最早的一种平衡树，不过现在平衡树的应用基本都是红黑树。

• 平衡树 又被称之为 二叉平衡树、平衡二叉树、平衡二叉搜索树等。

1. 除了规定左节点小于根节点，右节点大于根节点以外。
2. 还规定了左子树和右子树的高度相差不能超过 1。

• 平衡因子：左子树的高度减去其右子树的高度
• 所以平衡二叉树中，各个节点的平衡因子的绝对值小于等于1（-1，0，1）。
• 就可以满足我们的二叉平衡树条件，平衡二叉树是一颗二叉搜索树，只不过比较矮而已。
  

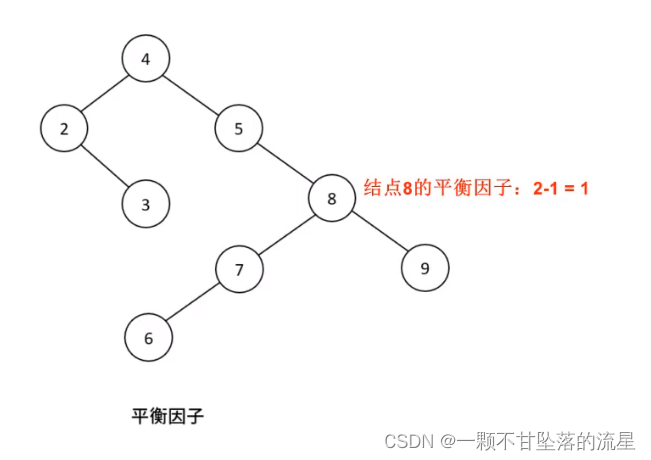
如果平衡因子的绝对值超过1，那么就称之为失衡，我们插入数据的时候，节点需要随时添加、随时删除，这样就会导致平衡二叉树出现失衡。

控制平衡因子：要把平衡因子控制在绝对值不大于1的范围内（平衡调整），在平衡二叉树中，使用旋转操作来达到平衡。

红黑树

AVL树相对于红黑树，它的插入/删除操作效率都不高，所以整体效率不如红黑树。
红黑树（R-B tree）是一种自平衡的二叉平衡搜索树，以前叫做平衡二叉B树

• 红黑树相比AVL树，新增了一些特性，正是这5个特性保证了红黑树的平衡性：

1. 节点是红色或者黑色（好比节点上有一个color属性在控制）
2. 根节点是黑色
3. 叶子节点都是黑色的空节点（null节点）
4. 每个红色节点的两个子节点都是黑色，不能有 2 个红色节点直接相连。
5. 从任意节点出发，到其每个叶子节点的路径中包含相同数据的黑色节点。
（是为了保证从根节点到叶子节点的最长路径不大于最短路径的 2 倍）

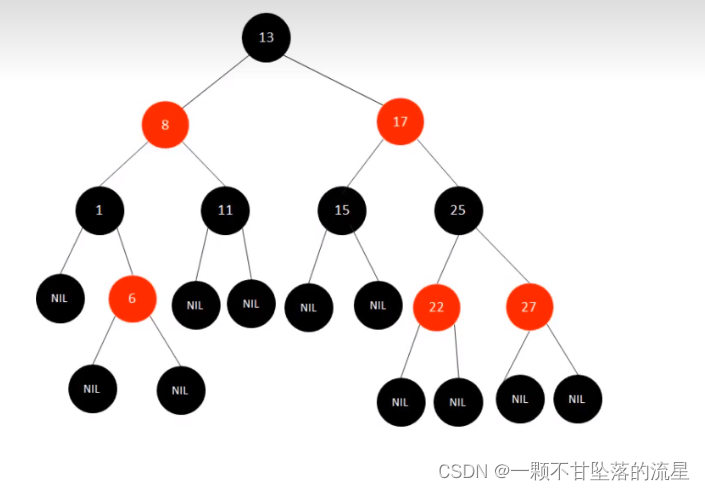
• 红黑树插入数据的时候，会先去遍历数据应该插入到哪个位置，插入的节点一定是红色的。

1. 因为如果插入的节点为红色的时候，有可能插入的是一次不违法红黑树任何规则的节点

2. 而插入黑色节点，必然会导致右一条路径上多了个黑色节点，这种比较难调整

3. 红色节点虽然可能导致出现红红相连的情况，但是这种情况可以通过颜色调换和旋转来调整

• 比如：要插入一个129的数值到红黑树里面：

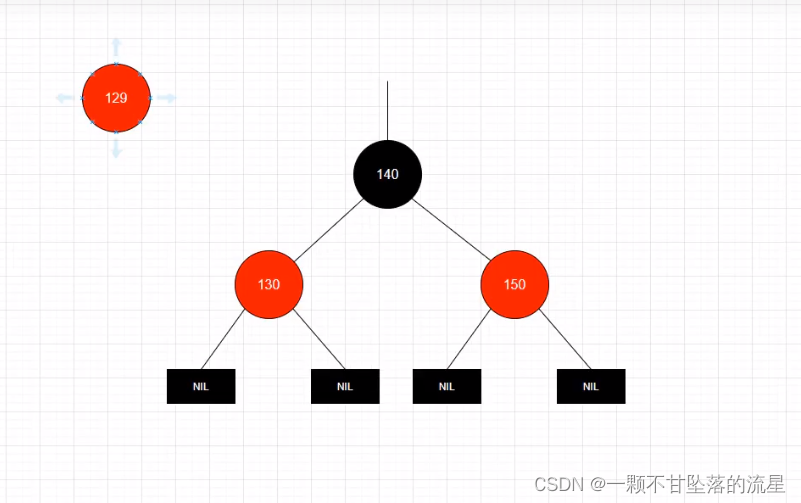
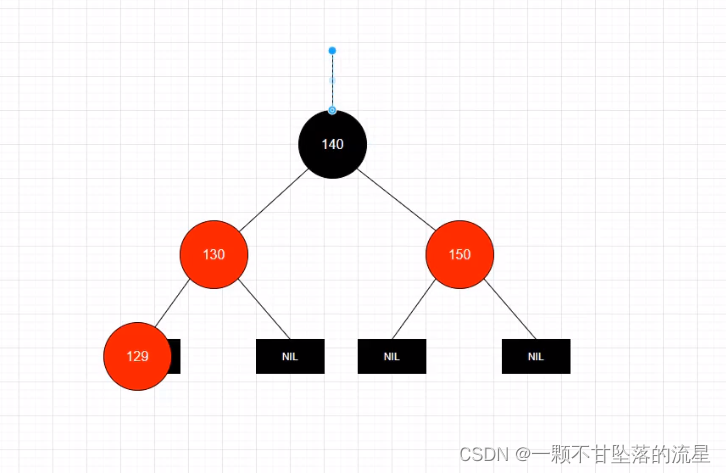
• 但是这种违背了红黑树的特性，经过变色调整后，让它符合5个特性：

• 红黑树的平衡调整有两种方式：变色，旋转（左旋转和右旋转）
  

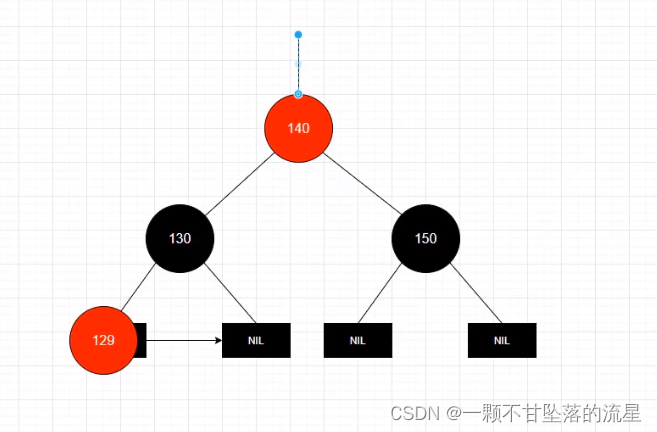
• 插入的129节点下面还要添加2个黑色的null节点，这时候就符合了红黑树的特性了