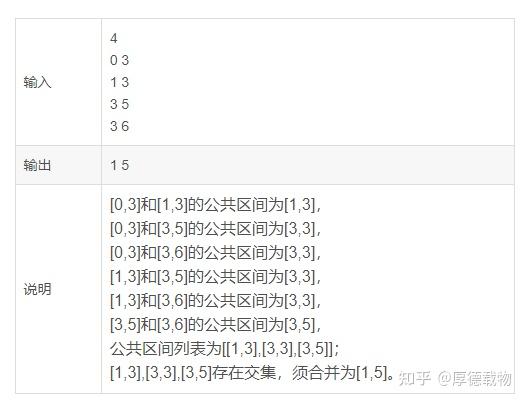
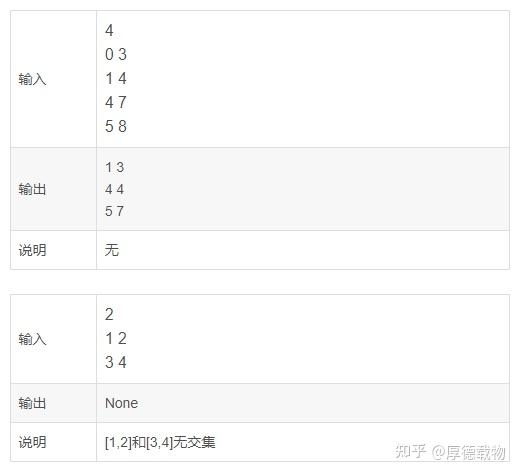
题目描述

给定一组闭区间，其中部分区间存在交集。

任意两个给定区间的交集，称为公共区间(如:[1,2],[2,3]的公共区间为[2,2],[3,5],[3,6]的公共区间为[3,5])公共区间之间若存在交集，则需要合并(如:[1,3],[3,5]区间存在交集[3,3],需合并为[1,5])。按升序排列输出合并后的区间列表

输入描述

组区间列表

区间数为 N: O<=N<=1000。

区间元素为 X:-10000<=X<=10000。

输出描述

升序排列的合并区间列表

备注

1、区间元素均为数字，不考虑字母、符号等异常输入。

2、单个区间认定为无公共区间。

用例

一、问题分析

首先读题，仔细看描述中的内容，发现需求是

1.给定一组闭区间，其中部分区间存在交集。

2.任意两个给定区间的交集，称为公共区间。

3.公共区间之间若存在交集，则需要合并，按升序排列输出合并后的区间列表

4.输入描述：组区间列表区间数为N，大于等于0小于等于1000.

区间元素为X，大于等于-10000小于等于10000

5.输入描述：升序排列的合并区间列表

6.备注：（1）区间元素均为数字，不考虑字母、符号等异常输入

（2）单个区间认为无公共区间。

二、解题思路

1.首先我们读取数据int N;区间数

scanf("%d", &N);

2.之后开始读取区间元素

int X[N][2];

for(int i = 0; i < N; i++) {

scanf("%d %d", &X[i][0], &X[i][1]);

}

3.然后我们计算公共区间

int Y[N * N][2];

int idx = 0;

for(int i = 0; i < N; i++) {

for(int j = i + 1; j < N; j++) {

// 如果比较小的值大于下一个区间比较大的值的时候没有交集

// 如果比较大的值小于下一个区间比较小的值的时候没有交集

// 比较小或者比较大的值有一个在下一个区间内的时候有交集

// 如果比较小的值大于下一个区间比较小的值但是小于下一个区间比较大的值

// 证明至少有一个数相交，公共区间从X[i][0]开始

// 比如第一个区间是1 3 第二个区间是0 4，1比0大比4小，3比4小，所以整个第一个区间都是贡藕给你区间

if(X[i][0] >= X[j][0] && X[i][0] <= X[j][1]) {

// 如果前一个区间的比较大的值小于等于后一个区间比较大的值，那么整个前一个区间都是公共区间

if(X[i][1] <= X[j][1]) {

Y[idx][0] = X[i][0];

Y[idx++][1] = X[i][1];

} 

//如果前一个区间比较大的值大于后一个区间比较大的值，那么它们的公共区间是从前一个数字比较小的值到后一个数字比较大的值

else {

Y[idx][0] = X[i][0];

Y[idx++][1] = X[j][1];

}

}

// 比如第一个区间是1 3 第二个区间是2 4,此时已经证明1不在2，4之间，

// 且3在2，4之间，那么我们的交集就是2，3

else if(X[i][1] >= X[j][0] && X[i][1] <= X[j][1]) {

Y[idx][0] = X[j][0];

Y[idx++][1] = X[i][1];

}

else if(X[j][0] >= X[i][0] && X[j][0] <= X[i][1]) {

if(X[j][1] <= X[i][1]) {

Y[idx][0] = X[j][0];

Y[idx++][1] = X[j][1];

} 

else {

Y[idx][0] = X[j][0];

Y[idx++][1] = X[i][1];

}

}

else if(X[j][1] >= X[i][0] && X[j][1] <= X[i][1]) {

Y[idx][0] = X[i][0];

Y[idx++][1] = X[j][1];

}

}

}

4.然后我们要合并公共区间,首先我们对公共空间进行一个排序

qsort(Y, idx, sizeof(Y[0]), compare);

int Z[idx][2];

int idxz = 0;

for(int i = 0; i < idx; i++) {

Z[idxz][0] = Y[i][0];

while(i < idx && Y[i][1] >= Y[i + 1][0]) {

i++;

}

i--;

Z[idxz++][1] = Y[i][1];

}

5.输出结果

if(idx == 0) printf("None\n");

else {

for(int i = 0; i < idxz; i++) {

printf("%d %d\n", Z[i][0], Z[i][1]);

}

}

三、具体步骤

使用的语言是C

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 比较函数，用于qsort按照区间起始值从小到大排序
int compare(const void* a, const void* b) {
    int (*arr_a)[2] = (int (*)[2])a;
    int (*arr_b)[2] = (int (*)[2])b;
    int result = (*arr_a)[0] - (*arr_b)[0];
    if(result == 0) {
        return ((*arr_a)[1] - (*arr_b[1]));
    }
    return result;
}

int main() {
    int N;
    scanf("%d", &N);
    // 动态分配内存用于存储区间数据
    int** X = (int**)malloc(N * sizeof(int*));
    for (int i = 0; i < N; i++) {
        X[i] = (int*)malloc(2 * sizeof(int));
    }

    // 读取区间元素
    for (int i = 0; i < N; i++) {
        scanf("%d %d", &X[i][0], &X[i][1]);
    }

    // 计算公共区间，使用动态分配内存的数组来存储
    int** Y = (int**)malloc(N * N * sizeof(int*));
    for (int i = 0; i < N * N; i++) {
        Y[i] = (int*)malloc(2 * sizeof(int));
    }
    int idx = 0;
    for (int i = 0; i < N; i++) {
        for (int j = i + 1; j < N; j++) {
            // 简化的区间相交判断逻辑，先确定两个区间的最小值和最大值
            int min_start = (X[i][0] < X[j][0]) ? X[i][0] : X[j][0];
            int max_start = (X[i][0] > X[j][0]) ? X[i][0] : X[j][0];
            int min_end = (X[i][1] < X[j][1]) ? X[i][1] : X[j][1];
            int max_end = (X[i][1] > X[j][1]) ? X[i][1] : X[j][1];

            if (max_start <= min_end) {
                // 存在交集，计算公共区间并存入Y数组
                Y[idx][0] = max_start;
                Y[idx][1] = min_end;
                idx++;
            }
        }
    }

    // 对公共区间数组Y进行排序
    qsort(Y, idx, sizeof(Y[0]), compare);

    // 合并公共区间，使用动态分配内存的数组来存储合并后的区间
    int** Z = (int**)malloc(idx * sizeof(int*));
    for (int i = 0; i < idx; i++) {
        Z[i] = (int*)malloc(2 * sizeof(int));
    }
    int idxz = 0;
    for (int i = 0; i < idx; ) {
        Z[idxz][0] = Y[i][0];
        int end = Y[i][1];
        int j = i + 1;
        while (j < idx && Y[j][0] <= end) {
            if (Y[j][1] > end) {
                end = Y[j][1];
            }
            j++;
        }
        Z[idxz][1] = end;
        idxz++;
        i = j;
    }

    // 输出结果
    if (idx == 0) {
        printf("None\n");
    } else {
        for (int i = 0; i < idxz; i++) {
            printf("%d %d\n", Z[i][0], Z[i][1]);
        }
    }

    // 释放动态分配的内存
    for (int i = 0; i < N; i++) {
        free(X[i]);
    }
    free(X);
    for (int i = 0; i < N * N; i++) {
        free(Y[i]);
    }
    free(Y);
    for (int i = 0; i < idx; i++) {
        free(Z[i]);
    }
    free(Z);

    return 0;
}