难度:简单
有
n座山排成一列,每座山都有一个高度。给你一个整数数组height,其中height[i]表示第i座山的高度,再给你一个整数threshold。对于下标不为
0的一座山,如果它左侧相邻的山的高度 严格大于threshold,那么我们称它是 稳定 的。我们定义下标为0的山 不是 稳定的。请你返回一个数组,包含所有 稳定 山的下标,你可以以 任意 顺序返回下标数组。
示例 1:
输入:height = [1,2,3,4,5], threshold = 2
输出:[3,4]
解释:
- 下标为 3 的山是稳定的,因为
height[2] == 3大于threshold == 2。- 下标为 4 的山是稳定的,因为
height[3] == 4大于threshold == 2.示例 2:
输入:height = [10,1,10,1,10], threshold = 3
输出:[1,3]
示例 3:
输入:height = [10,1,10,1,10], threshold = 10
输出:[]
提示:
2 <= n == height.length <= 1001 <= height[i] <= 1001 <= threshold <= 100
题解:class Solution: def stableMountains(self, height: List[int], threshold: int) -> List[int]: res = [] for i in range(1,len(height)): if height[i-1] > threshold: res.append(i) return res
leetcode:3285. 找到稳定山的下标(python3解法)
news2026/2/13 15:48:30
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/2262889.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
深度学习之超分辨率算法——SRGAN
更新版本 实现了生成对抗网络在超分辨率上的使用 更新了损失函数,增加先验函数 SRresnet实现
import torch
import torchvision
from torch import nnclass ConvBlock(nn.Module):def __init__(self, kernel_size3, stride1, n_inchannels64):super(ConvBlock…
集成方案 | Docusign + 金蝶云,实现合同签署流程自动化!
本文将详细介绍 Docusign 与金蝶云的集成步骤及其效果,并通过实际应用场景来展示 Docusign 的强大集成能力,以证明 Docusign 集成功能的高效性和实用性。 在当今商业环境中,流程的无缝整合与数据的实时性对于企业的成功至关重要。金蝶云&…
数据结构----链表头插中插尾插
一、链表的基本概念
链表是一种线性数据结构,它由一系列节点组成。每个节点包含两个主要部分:
数据域:用于存储数据元素,可以是任何类型的数据,如整数、字符、结构体等。指针域:用于存储下一个节点&#…
Service Discovery in Microservices 客户端/服务端服务发现
原文链接 Client Side Service Discovery in Microservices - GeeksforGeeks
原文链接 Server Side Service Discovery in Microservices - GeeksforGeeks
目录
服务发现介绍
Server-Side 服务发现
实例:
Client-Side 服务发现
实例: 服务发现介绍…
Git连接远程仓库(超详细)
目录
一、Gitee 远程仓库连接
1. HTTPS 方式
2. SSH公钥方式
(1)账户公钥
(2)仓库公钥
仓库的 SSH Key 和账户 SSH Key 的区别?
二、GitHub远程仓库连接
1. HTTPS方式
2.SSH公钥方式 本文将介绍如何通过 H…
系列4:基于Centos-8.6 Kubernetes多网卡节点Calico选择网卡配置
每日禅语 不动心”是一个人修养和定力的体现,若一个人心无定力,就会被外界环境左右,随外界的境遇而动摇。佛家认为,心是一切的基础,一个人如果想要真正入定,必须先从修心开始。修心即是净心,心灵…
Docker:Dockerfile(补充四)
这里写目录标题 1. Dockerfile常见指令1.1 DockerFile例子 2. 一些其他命令 1. Dockerfile常见指令 简单的dockerFile文件
FROM openjdk:17LABEL authorleifengyangCOPY app.jar /app.jarEXPOSE 8080ENTRYPOINT ["java","-jar","/app.jar"]# 使…
98. 验证二叉搜索树(java)
题目描述:
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左 子树 只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。 …
微软 Phi-4:小型模型的推理能力大突破
在人工智能领域,语言模型的发展日新月异。微软作为行业的重要参与者,一直致力于推动语言模型技术的进步。近日,微软推出了最新的小型语言模型 Phi-4,这款模型以其卓越的复杂推理能力和在数学领域的出色表现,引起了广泛…
libaom 源码分析:熵编码模块介绍
AV1 熵编码原理介绍 关于AV1 熵编码原理介绍可以参考:AV1 编码标准熵编码技术概述libaom 熵编码相关源码介绍
函数流程图 核心函数介绍 av1_pack_bitstream 函数:该函数负责将编码后的数据打包成符合 AV1 标准的比特流格式;包括写入序列头 OBU 的函数 av1_write_obu_header…
JAVA基于百度AI人脸识别签到考勤系统(开题报告+作品+论文)
博主介绍:黄菊华老师《Vue.js入门与商城开发实战》《微信小程序商城开发》图书作者,CSDN博客专家,在线教育专家,CSDN钻石讲师;专注大学生毕业设计教育、辅导。 所有项目都配有从入门到精通的基础知识视频课程ÿ…
go 中使用redis 基础用法
1、安装redis
参考链接:https://www.codeleading.com/article/98554130215/
1.1 查看是否有redis yum 源
yum install redis没有可用的软件包,执行1.2
1.2下载fedora的epel仓库
yum install epel-release --下载fedora的epel仓库1.3启动redis
s…
简易记事本开发-(SSM+Vue)
目录 前言
一、项目需求分析
二、项目环境搭建 1.创建MavenWeb项目: 2.配置 Spring、SpringMVC 和 MyBatis
SpringMVC 配置文件 (spring-mvc.xml): 配置视图解析器、处理器映射器,配置了CORS(跨源资源共享)&#x…
vsCode 报错[vue/no-v-model-argument]e‘v-model‘ directives require no argument
在vue3中使用ui库中的组件语法v-model:value时会提示[vue/no-multiple-template-root]The template root requires exactly one element. 引入组件使用单标签时会提示[vue/no-multiple-template-root]“The template root requires exactly one element.
原因: 1.可…
初学stm32 -- SysTick定时器
以delay延时函数来介绍SysTick定时器的配置与使用
首先是delay_init()延时初始化函数,这个函数主要是去初始化SysTick定时器;
void delay_init()
{SysTick_CLKSourceConfig(SysTick_CLKSource_HCLK_Div8); //选择外部时钟 HCLK/8fac_usSystemCoreCloc…
Gitlab 数据备份全攻略:命令、方法与注意事项
文章目录 1、备份命令2、备份目录名称说明3、手工备份配置文件3.1 备份配置文件3.2 备份ssh文件 4、备份注意事项4.1 停止puma和sicdekiq组件4.2 copy策略需要更多磁盘空间 5、数据备份方法5.1 docker命令备份5.2 kubectl命令备份5.3 参数说明5.4、选择性备份5.5、非tar备份5.6…
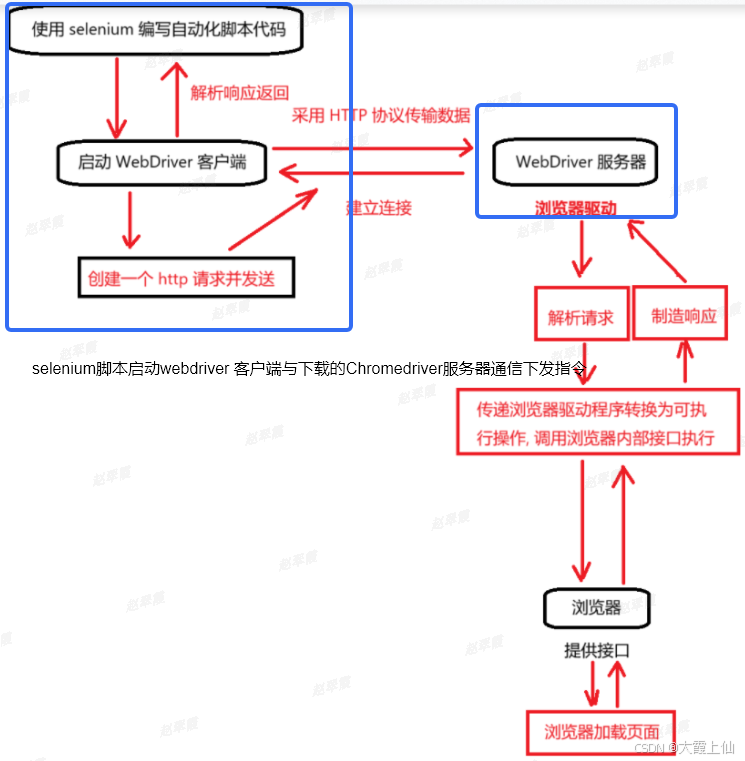
selenium工作原理
原文链接:https://blog.csdn.net/weixin_67603503/article/details/143226557 启动浏览器和绑定端口 当你创建一个 WebDriver 实例(如 webdriver.Chrome())时,Selenium 会启动一个新的浏览器实例,并为其分配一个特定的…
Docker--Docker Registry(镜像仓库)
什么是Docker Registry?
镜像仓库(Docker Registry)是Docker生态系统中用于存储、管理和分发Docker镜像的关键组件。 镜像仓库主要负责存储Docker镜像,这些镜像包含了应用程序及其相关的依赖项和配置,是构建和运行Doc…
OpenEuler Linux上怎么测试Nvidia显卡安装情况
当安装好显卡驱动后怎么样知道驱动程序安装好了,这里以T400 OpenEuler 正常情况下,我们只要看一下nvidia-smi 状态就可以确定他已经正常了 如图:
这里就已经确定是可以正常使用了,这里只是没有运行对应的程序,那接来下我们就写一个测试程序来测试一下:以下代码通过AI给出然后…















![vsCode 报错[vue/no-v-model-argument]e‘v-model‘ directives require no argument](https://i-blog.csdnimg.cn/direct/be74560078fb44a19ec7a5ca2aa48713.png)