PCA 原理推导

news2024/11/16 9:23:31

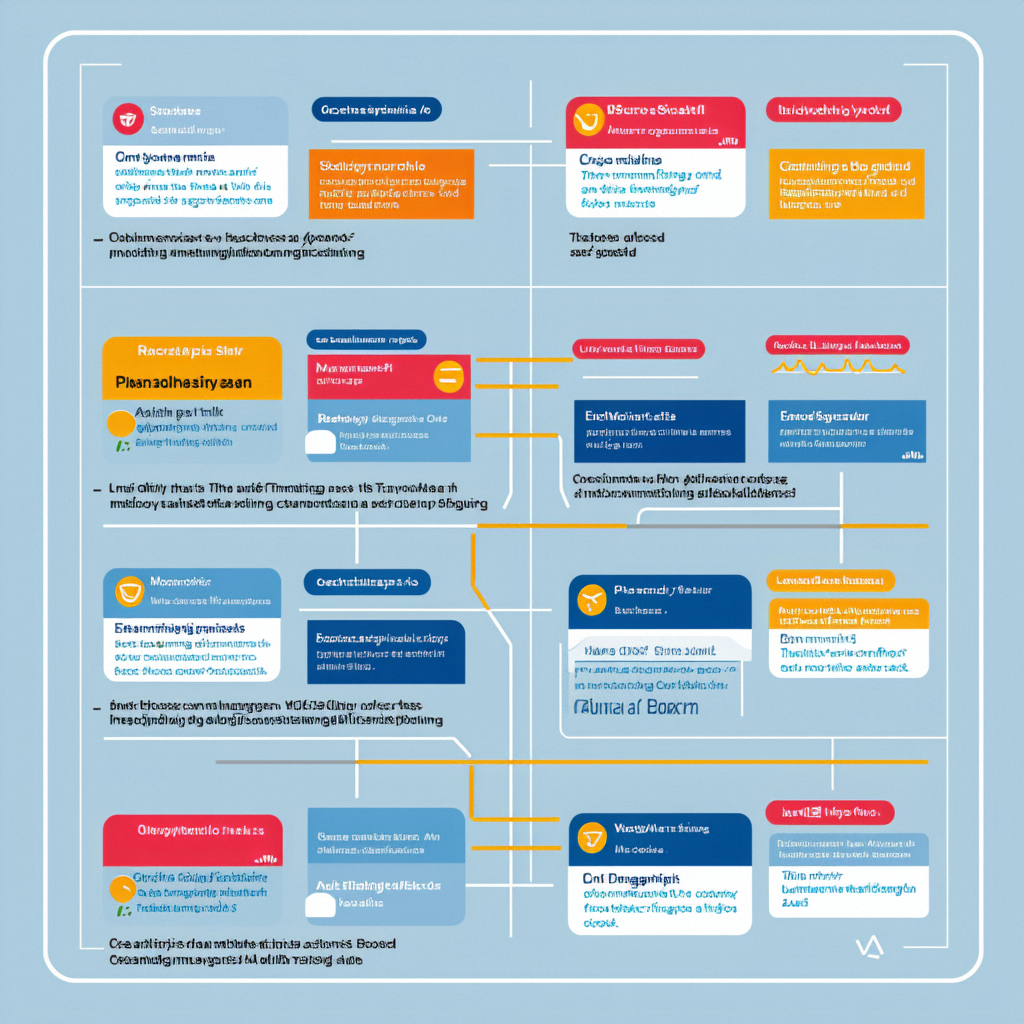
针对高维数据的降维问题，PCA 的基本思路如下：首先将需要降维的数据的各个变量标准化（规范化）为均值为 0，方差为 1 的数据集，然后对标准化后的数据进行正交变换，将原来的数据转换为若干个线性无关向量表示的新数据：这些新向量表示的数据不仅要求相互线性无关，而且需要所包含的信息量最大。PCA 的一个示例如图 18-1 所示。
图 18-1 PCA 示例
图 18-1 中，左图是一组由变量 $x_1$ 和 $x_2$ 表示的二维空间，数据分布于图中椭圆形区域内，能够看到，变量 $x_1$ 和 $x_2$ 存在一定的相关关系；右图是对数据进行正交变换后的数据坐标系中，向变量 $y_1$ 和 $y_2$ 表示。为了使得变换后的信息量最大，PCA 使用方差最大的方向作为新坐标系的第一坐标轴 $y_1$ ，方差第二大的作为第二坐标轴 $y_2$ 。

PCA 使用方差衡量新变量的信息量大小，按照方差大小排序依次为第一主成分、第二主成分、⋯⋯，下面对 PCA 原理进行简单推导。

假设原始数据为 m 维随机变量 $(x_1, x_2, \cdots, x_m)^\top$ ，其均值向量 $\mu = E(x) = (\mu_1, \mu_2, \cdots, \mu_m)^\top$ ，协方差矩阵为：

$\Sigma = \operatorname{cov}(x, x) = E \left[ (x - \mu)(x - \mu)^\top \right] \tag{18-1}$

由 m 维随机变量 $x$ 到 m 维随机变量 $(y_1, y_2, \cdots, y_m)^\top$ 的线性变换：

$y_i = a_i^\top x = a_{i1} x_1 + a_{i2} x_2 + \cdots + a_{im} x_m \tag{18-2}$

其中 $a_i^\top = (a_{i1}, a_{i2}, \cdots, a_{im})$ 。

经线性变换后的随机变量 $y_i$ 的均值、方差和协方差统计量可以表示为：

$E(y_i) = a_i^\top \mu, \quad i = 1, 2, \cdots, m \tag{18-3}$

$\operatorname{var}(y_i) = a_i^\top \Sigma a_i, \quad i = 1, 2, \cdots, m \tag{18-4}$

$\operatorname{cov}(y_i, y_j) = a_i^\top \Sigma a_j, \quad i, j = 1, 2, \cdots, m \tag{18-5}$

当随机变量 $x$ 到随机变量 $y$ 的线性变换满足如下条件时，变换后的 $y_1, y_2, \cdots, y_m$ 分别为随机变量 $x$ 的第一主成分、第二主成分、⋯⋯、第 m 主成分。

线性变换的系数向量 $a_i$ 为单位向量，有 $a_i^\top a_i = 1, \ i = 1, 2, \cdots, m$ 。
线性变换后的变量 $y_i$ 与 $y_j$ 线性无关，即 $\operatorname{cov}(y_i, y_j) = 0(i \neq j)$ 。
变量 $y_i$ 是随机变量 $x$ 所有线性变换中方差最大的， $y_2$ 是与 $y_1$ 无关的所有线性变换中方差最大的。

上述三个条件给出了求解主成分的基本方法。根据优化目标和约束条件，我们可以使用拉格朗日乘子法来求解主成分。下面以第一主成分为例进行求解推导。第一主成分的优化问题的数学表达为：

$\max \quad a_1^\top \Sigma a_1 \tag{18-6}$

$\quad a_1^\top a_1 = 1 \tag{18-7}$

定义拉格朗日目标函数如下：

$a_1^\top \Sigma a_1 - \lambda (a_1^\top a_1 - 1) \tag{18-8}$

将式 (18-8) 的拉格朗日函数对 $a_1$ 求导并令其为 0，有：

$\frac{\partial L}{\partial a_1} = \Sigma a_1 - \lambda a_1 = 0 \tag{18-9}$

根据矩阵特征值与特征向量的关系，由式 (18-9) 可知 $\lambda$ 为 $\Sigma$ 的特征值， $a_1$ 为对应的单位特征向量。假设 $a_1$ 是 $\Sigma$ 的最大特征值 $\lambda_1$ 对应的单位特征向量，那么 $a_1$ 和 $\lambda_1$ 均为上述优化问题的最优解。所以 $a_1^Tx$ 为第一主成分，其方差为对应协方差矩阵的最大特征值：