一、题目描述
给你一个数组 rectangles ,其中 rectangles[i] = [xi, yi, ai, bi] 表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (xi, yi) ,右上顶点是 (ai, bi) 。
如果所有矩形一起精确覆盖了某个矩形区域,则返回 true ;否则,返回 false 。
示例 1:

输入:rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]] 输出:true 解释:5 个矩形一起可以精确地覆盖一个矩形区域。
示例 2:
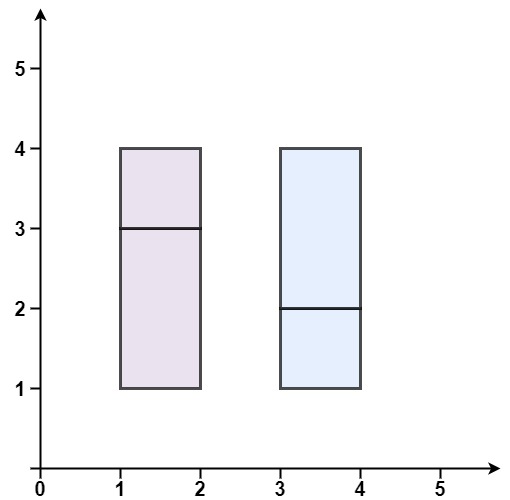
输入:rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]] 输出:false 解释:两个矩形之间有间隔,无法覆盖成一个矩形。
示例 3:
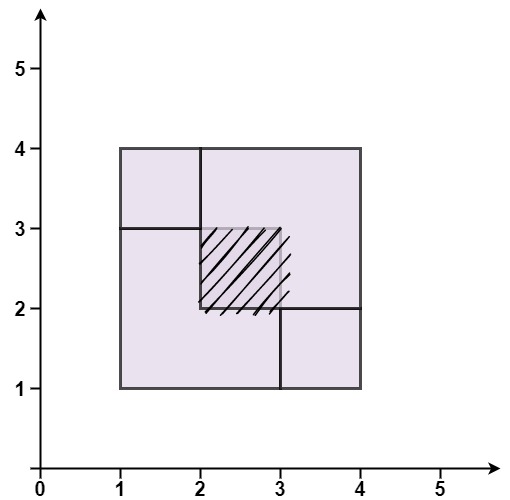
输入:rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]] 输出:false 解释:因为中间有相交区域,虽然形成了矩形,但不是精确覆盖。
提示:
1 <= rectangles.length <= 2 * 10^4rectangles[i].length == 4-10^5 <= xi < ai <= 10^5-10^5 <= yi < bi <= 10^5
二、解题思路
- 首先,我们可以计算出所有矩形的总面积,记为
totalArea。 - 然后,我们需要找到能够被所有矩形覆盖的最小矩形的边界。这个矩形的左下角顶点将是所有给定矩形左下角顶点的最小值,右上角顶点将是所有给定矩形右上角顶点的最大值。
- 计算这个最小矩形的面积,记为
expectedArea。 - 如果
totalArea不等于expectedArea,那么直接返回false,因为矩形的总面积不匹配。 - 为了检查矩形是否精确覆盖,我们还需要确保矩形的边缘没有重叠或间隙。我们可以使用一个集合来记录所有矩形的边缘。对于每个矩形,我们添加它的四个边到集合中,如果这条边已经存在于集合中,则移除它(表示这条边被覆盖了两次,即两个矩形的边缘重合)。最后,集合中应该只剩下四个边,它们分别是组成最小矩形的四条边。
- 最后,检查集合中的边是否与最小矩形的边匹配。
三、具体代码
import java.util.HashSet;
import java.util.Set;
class Solution {
public boolean isRectangleCover(int[][] rectangles) {
int lx = Integer.MAX_VALUE, ly = Integer.MAX_VALUE, rx = Integer.MIN_VALUE, ry = Integer.MIN_VALUE;
int totalArea = 0;
Set<String> edges = new HashSet<>();
for (int[] rect : rectangles) {
lx = Math.min(lx, rect[0]);
ly = Math.min(ly, rect[1]);
rx = Math.max(rx, rect[2]);
ry = Math.max(ry, rect[3]);
totalArea += (rect[2] - rect[0]) * (rect[3] - rect[1]);
String[] edgeKeys = {
rect[0] + " " + rect[1],
rect[0] + " " + rect[3],
rect[2] + " " + rect[1],
rect[2] + " " + rect[3]
};
for (String key : edgeKeys) {
if (!edges.add(key)) {
edges.remove(key);
}
}
}
int expectedArea = (rx - lx) * (ry - ly);
if (totalArea != expectedArea) {
return false;
}
String[] finalEdges = {
lx + " " + ly,
lx + " " + ry,
rx + " " + ly,
rx + " " + ry
};
for (String edge : finalEdges) {
if (!edges.contains(edge)) {
return false;
}
}
return edges.size() == 4;
}
}
在这个代码中,我们使用了一个字符串来表示矩形的边,格式为 “x y”,其中 x 和 y 是矩形的横纵坐标。通过这种方式,我们可以将矩形的边作为唯一的标识符添加到集合中。
四、时间复杂度和空间复杂度
1. 时间复杂度
-
我们遍历了整个
rectangles数组,其中包含n个矩形。每个矩形我们进行常数时间的操作,例如更新边界坐标、计算面积和更新集合edges。因此,这部分的时间复杂度是 O(n)。 -
对于每个矩形,我们添加或移除四条边到集合
edges中。集合add和remove操作的平均时间复杂度是 O(1)。 -
在最后,我们检查集合
edges的大小和内容,这也是常数时间操作。
综上所述,整体的时间复杂度是 O(n),其中 n 是矩形数组的长度。
2. 空间复杂度
-
我们使用了几个变量来存储边界坐标和总面积,这些变量占用的空间是常数,即 O(1)。
-
我们使用了一个
HashSet集合edges来存储矩形的边。在最坏的情况下,如果所有的矩形边都不重合,那么集合的大小将是 4n(每个矩形有4条边)。因此,空间复杂度是 O(n)。
综上所述,整体的空间复杂度是 O(n),其中 n 是矩形数组的长度。
五、总结知识点
-
Java 基础语法:
- 类定义(
class关键字) - 方法定义(
public访问修饰符,返回类型,方法名,参数列表) - 变量声明与初始化(基本数据类型,如
int) - 数组的使用(通过索引访问数组元素)
- 类定义(
-
Java 集合框架:
HashSet类的使用,用于存储唯一的元素集合- 集合的基本操作,如
add(添加元素)和remove(移除元素) contains方法,用于检查集合中是否包含某个元素
-
数学运算:
- 计算矩形的面积(通过长和宽的乘积)
- 使用
Math.min和Math.max方法来找到最小和最大的边界值
-
字符串操作:
- 字符串拼接(使用
+运算符连接字符串) - 使用字符串作为集合中元素的键,以表示矩形的边
- 字符串拼接(使用
-
逻辑控制:
- 循环结构(
for循环,用于遍历矩形数组) - 条件语句(
if语句,用于检查条件并作出决策)
- 循环结构(
以上就是解决这个问题的详细步骤,希望能够为各位提供启发和帮助。