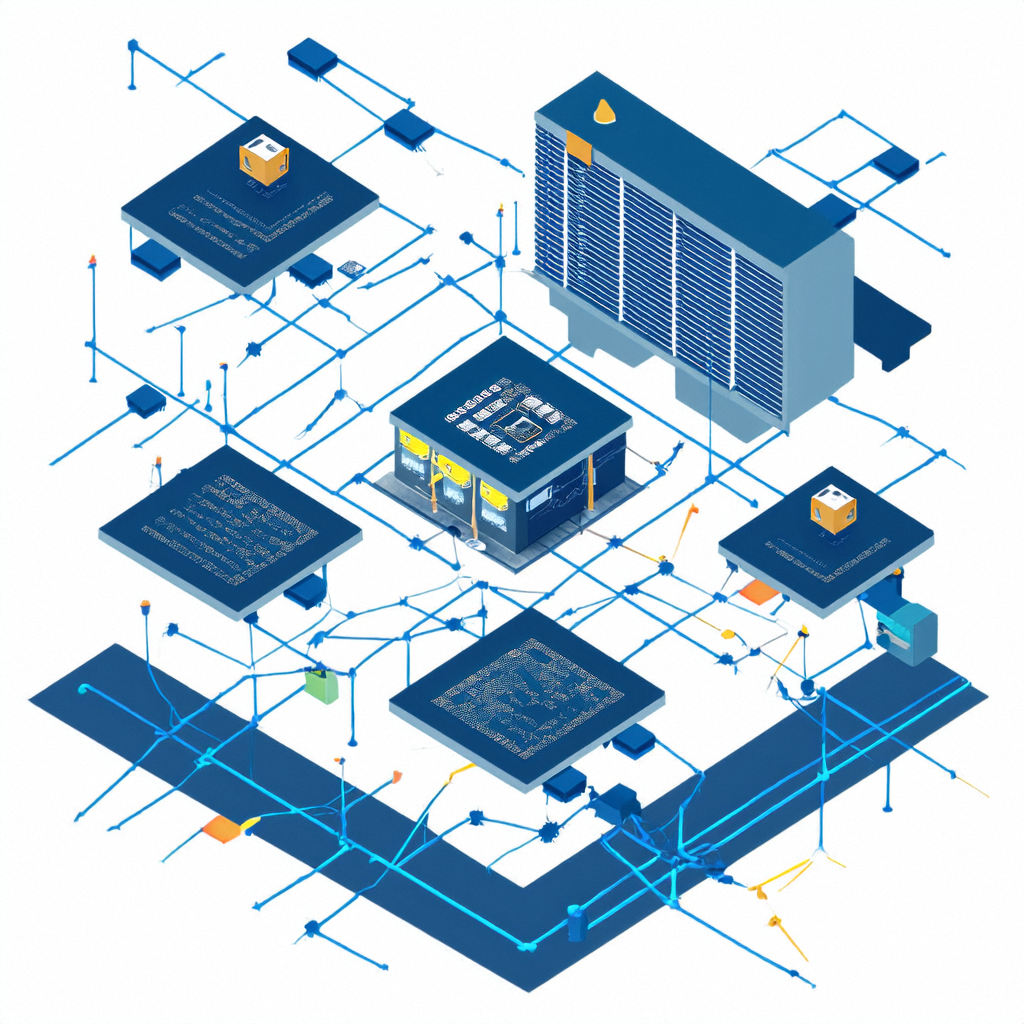
图1:同步发电机稳态相量图
若发电机为凸极式,由于凸极机正、交轴同步电抗不等,即xd≠xq,因此必须先借助虚构电动势
E
˙
Q
=
E
˙
q
−
(
x
d
−
x
q
)
I
˙
d
\dot{E}_Q=\dot{E}_q-(x_d-x_q)\dot{I}_d
E˙Q=E˙q−(xd−xq)I˙d来确定交轴的正方向,再在
E
˙
Q
\dot{E}_Q
E˙Q的延长线上按上述关系求出空载电动势
E
˙
q
\dot{E}_q
E˙q,之所以借助虚构电动势
E
˙
Q
\dot{E}_Q
E˙Q是由于凸极式同步机有:
注意下面是数值关系(对照图1的相量图分析下),电感是需要转90°:
{
I
d
=
E
q
−
U
q
x
d
I
q
=
U
d
x
q
\left\{\begin{array}{l} I_{\mathrm{d}}=\frac{E_{\mathrm{q}}-U_{\mathrm{q}}}{x_{\mathrm{d}}} \\ I_{\mathrm{q}}=\frac{U_{\mathrm{d}}}{x_{\mathrm{q}}} \end{array}\right.
{Id=xdEq−UqIq=xqUd
{ U d = I q x q U q = E q − I d x d = E Q − I d x q \left\{\begin{array}{l} U_{\mathrm{d}}=I_{\mathrm{q}} x_{\mathrm{q}} \\ U_{\mathrm{q}}=E_{\mathrm{q}}-I_{\mathrm{d}} x_{\mathrm{d}}=E_{\mathrm{Q}}-I_{\mathrm{d}} x_{\mathrm{q}} \end{array}\right. {Ud=IqxqUq=Eq−Idxd=EQ−Idxq
之后再构造成相量形式
U
d
+
j
U
q
=
I
q
x
q
+
j
(
E
Q
−
I
d
x
q
)
U
d
+
j
U
q
+
j
I
d
x
q
+
j
⋅
j
I
q
x
q
=
j
E
Q
j
E
Q
=
(
U
d
+
j
U
q
)
+
j
x
q
(
I
d
+
j
I
q
)
E
˙
Q
=
U
˙
+
j
x
q
I
˙
\begin{aligned} & U_{\mathrm{d}}+\mathrm{j} U_{\mathrm{q}}=I_{\mathrm{q}} x_{\mathrm{q}}+\mathrm{j}\left(E_{\mathrm{Q}}-I_{\mathrm{d}} x_{\mathrm{q}}\right) \\ & U_{\mathrm{d}}+\mathrm{j} U_{\mathrm{q}}+\mathrm{j} I_{\mathrm{d}} x_{\mathrm{q}}+\mathrm{j} ·\mathrm{j} I_{\mathrm{q}} x_{\mathrm{q}}=\mathrm{j} E_{\mathrm{Q}} \\ & \mathrm{j} E_{\mathrm{Q}}=\left(U_{\mathrm{d}}+\mathrm{j} U_{\mathrm{q}}\right)+\mathrm{j} x_{\mathrm{q}}\left(I_{\mathrm{d}}+\mathrm{j} I_{\mathrm{q}}\right) \\ & \dot{E}_{\mathrm{Q}}=\dot{U}+\mathrm{j} x_{\mathrm{q}} \dot{I} \end{aligned}
Ud+jUq=Iqxq+j(EQ−Idxq)Ud+jUq+jIdxq+j⋅jIqxq=jEQjEQ=(Ud+jUq)+jxq(Id+jIq)E˙Q=U˙+jxqI˙
这个虚拟电势EQ的目的就是为了快速确定Q轴,不用分解U和I相量。
最后再加一个分量即可得到真正的空载电动势Eq
U d = I q x q j U q = j ( E q − I d x d ) U d + j U q = I q x q + j ( E q − I d x d ) j E q = ( U d + j U q ) + j j I q x q + j I d x q − j I d x q + j I d x d j E q = ( U d + j U q ) + j x q ( I d + j I q ) + j I d ( x d − x q ) E ˙ q = U ˙ + j x q I ˙ ⏟ E ˙ Q + j I d ( x d − x q ) \begin{aligned} & U_{\mathrm{d}}=I_{\mathrm{q}} x_{\mathrm{q}} \\ & \mathrm{j} U_{\mathrm{q}}=\mathrm{j}\left(E_{\mathrm{q}}-I_{\mathrm{d}} x_{\mathrm{d}}\right) \\ & U_{\mathrm{d}}+\mathrm{j} U_{\mathrm{q}}=I_{\mathrm{q}} x_{\mathrm{q}}+\mathrm{j}\left(E_{\mathrm{q}}-I_{\mathrm{d}} x_{\mathrm{d}}\right) \\ & \mathrm{j} E_{\mathrm{q}}=\left(U_{\mathrm{d}}+\mathrm{j} U_{\mathrm{q}}\right)+\mathrm{jj} I_{\mathrm{q}} x_{\mathrm{q}}+\mathrm{j} I_{\mathrm{d}} x_{\mathrm{q}}-\mathrm{j} I_{\mathrm{d}} x_{\mathrm{q}}+\mathrm{j} I_{\mathrm{d}} x_{\mathrm{d}} \\ & \mathrm{j} E_{\mathrm{q}}=\left(U_{\mathrm{d}}+\mathrm{j} U_{\mathrm{q}}\right)+\mathrm{j} x_{\mathrm{q}}\left(I_{\mathrm{d}}+\mathrm{j} I_{\mathrm{q}}\right)+\mathrm{j} I_{\mathrm{d}}\left(x_{\mathrm{d}}-x_{\mathrm{q}}\right) \\ & \dot{E}_{\mathrm{q}}=\underbrace{\dot{U}+\mathrm{j} x_{\mathrm{q}} \dot{I}}_{\dot{E}_{\mathrm{Q}}}+\mathrm{j} I_{\mathrm{d}}\left(x_{\mathrm{d}}-x_{\mathrm{q}}\right) \end{aligned} Ud=IqxqjUq=j(Eq−Idxd)Ud+jUq=Iqxq+j(Eq−Idxd)jEq=(Ud+jUq)+jjIqxq+jIdxq−jIdxq+jIdxdjEq=(Ud+jUq)+jxq(Id+jIq)+jId(xd−xq)E˙q=E˙Q U˙+jxqI˙+jId(xd−xq)
因为 j I d ( x d − x q ) \mathrm{j} I_{\mathrm{d}}\left(x_{\mathrm{d}}-x_{\mathrm{q}}\right) jId(xd−xq)是在q轴上,因此通过EQ确定了q轴线后,再叠加一个数值量 I d ( x d − x q ) I_{\mathrm{d}}\left(x_{\mathrm{d}}-x_{\mathrm{q}}\right) Id(xd−xq)即可得到空载电动势Eq。

图2 含有EQ虚拟电势的相量图
大部分时候计算是以电压为参考∠0°,即把U相量水平放置,其实就是旋转了一下,关系式不变。
通过图2我们很快确定q轴位置,并得到空载电动势,空载电动势和负载电流的夹角为内功率因数角 ψ \psi ψ:
ψ 0 = tan − 1 ( U sin φ + I X q U cos φ + I R a ) \psi_0=\tan ^{-1}\left(\frac{U \sin \varphi+I X_q}{U \cos \varphi+I R_a}\right) ψ0=tan−1(Ucosφ+IRaUsinφ+IXq)
由于在计算的时候一般不考虑电阻,因此Ra=0,上述公式的 φ \varphi φ是定子电压即同步电机的输出电压和负载电流的夹角,称为外功率因数角。
通过图2的空间几何关系可以得到上式求得内功率因数角 ψ \psi ψ,内功率因数角 ψ \psi ψ和外功率因数角 φ \varphi φ的差值称为功角 δ \delta δ,就是这个角影响有功功率传输(有功和无功解耦的情况下)。