第二十三课 AlexNet

       AlexNet是在2012年被发表的一个金典之作，并在当年取得了ImageNet最好成绩，也是在那年之后，更多的更深的神经网路被提出，比如优秀的vgg,GoogleLeNet.

       其官方提供的数据模型，准确率达到57.1%,top 1-5 达到80.2%. 这项对于传统的机器学习分类算法而言，已经相当的出色。

目录

理论部分

实践部分

---

理论部分

       机器学习在2000年初期最主流的算法是核方法。其核心是：首先提取特征，然后用核函数计算相关性，也就是说如何判断在高维空间的两个点是如何相关的。核方法是通过拉伸空间把空间变成想要的样子。

       卷积神经网络通常用于处理图片，也就是计算机视觉。计算机视觉是从几何学过来的。

       特征工程在10-15年前是深度学习的主要手段，它探究图片抽取特征的方法。

       过去60年的发展趋势：

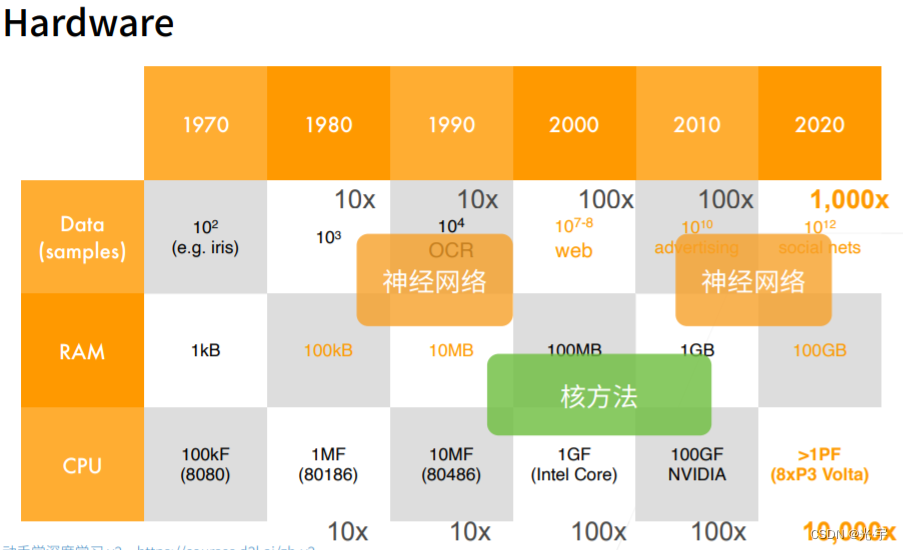
       深度神经网络的兴起离不开数据的进步。这里要提到一个非常著名的数据集——ImageNet，它主要用于物体分类，它和mnist数据集的主要区别是：它不是做黑白的手写数字的分类，而是做彩色自然物体的分类，每张图片的大小、样本数还有类数都要比mnist数据集复杂得多。

       因为数据集的扩大和复杂化，因此就允许我使用更深层的网络去抽取里面更复杂的信息。

       下面让我们来看看冠军数据集是如何处理更为复杂的数据集的。

       Alexnet其实本质上是个更深更大的lenet。

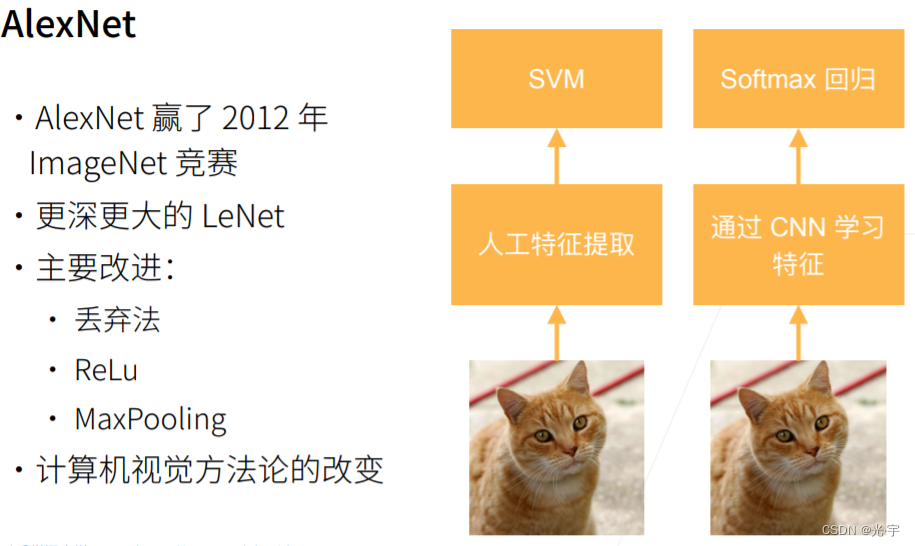
Alexnet能获得成功主要在于:

1、构造CNN相对来说比较简单，不需要了解太多计算机方面的知识，它还可以比较方便的跨到不同领域去解决问题；

2、CNN和softmax是一起训练的，可以更加高效。

下面是Alexnet和lenet的对比图：

相比于lenet，Alexnet的核窗口更大，步长更大（否则计算会很难），池化窗口更大，通道更多，层数稍多，隐藏层变大。

实践部分

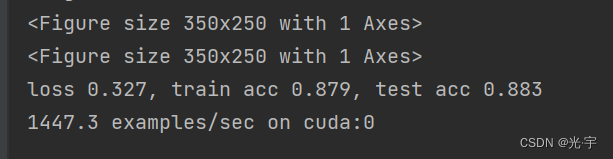
首先看一下 accuracy ，lenet测试的精度也是0.82，所以现在 Alex net 就直接把我的精度变到了 0.88 ，而且它的好处是没有太多 overfitting 在里面，这是因为学习率比较低，而且我们就跑了 10 epoch 其实loss 还在往下降。所以这一块 Alex 绝对是能够 overfeed 到这个数据集的，只是我们学习率比较低，然后没有跑很多次数据。所以 overfitting 还没有发生在这个地方，大家可以去把那个把学习率改大一点，应该是能看到过过拟合情况。所以但是另外一块就是说主要是我的精度有提升了。

第二个是说代价是什么？lenet训练速度大概是 9 万的，现在Alexnet的训练速度变成了4000，就是慢了 20 倍。所以为什么是说你enet计算量比Alexnet少个 200 倍的样子。但为什么这里只慢了 20 倍呢？是因为lenet太小了，它都无法使用我们的 GPU 的核，我们 GPU 有上千个核，就是说这个 lenet批量很小，然后卷积又很小，它的并行度很差，就是根本无法用上我们 GPU 上千个核。 so ，Alex 相对来说会好一点，但后面的网络更加是适合 GPU 计算。所以 alexnet 相对来说在 GPU 的使用率上，大概是百分之七八十。所以就意味着是我虽然比你计算量多了 200 倍，但实际上也就慢了 20 倍。而且你可以看到Alexnet这个其实不慢，每秒钟能够跑个 4000 个样本。如果你就算是 image net 的话，那么也就120 万个样本的话，那么也就是 3000 秒能跑完，就是将近一个小时能够跑迭代一次数据。在 MG net 上训练100 轮的话，那就是 100 个小时在单卡上也能跑完 100 个小时八九天的样子。所以就是 Alex net 一个性能，所以看到是慢的 20 倍精度从 0.8 涨到了0.88。

 code:

#深度卷积神经网络（AlexNet）
import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt
net = nn.Sequential(
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2), nn.Flatten(),
    nn.Linear(6400, 4096), nn.ReLU(), nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(p=0.5),
    nn.Linear(4096, 10))
#我们构造一个 单通道数据，来观察每一层输出的形状
X = torch.randn(1, 1, 224, 224)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__, 'Output shape:\t', X.shape)
#Fashion-MNIST图像的分辨率 低于ImageNet图像。 我们将它们增加到 224×224
batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
#训练AlexNet
lr, num_epochs = 0.01, 10
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
plt.show()

Conv2d Output shape:     torch.Size([1, 96, 54, 54])
ReLU Output shape:     torch.Size([1, 96, 54, 54])
MaxPool2d Output shape:     torch.Size([1, 96, 26, 26])
Conv2d Output shape:     torch.Size([1, 256, 26, 26])
ReLU Output shape:     torch.Size([1, 256, 26, 26])
MaxPool2d Output shape:     torch.Size([1, 256, 12, 12])
Conv2d Output shape:     torch.Size([1, 384, 12, 12])
ReLU Output shape:     torch.Size([1, 384, 12, 12])
Conv2d Output shape:     torch.Size([1, 384, 12, 12])
ReLU Output shape:     torch.Size([1, 384, 12, 12])
Conv2d Output shape:     torch.Size([1, 256, 12, 12])
ReLU Output shape:     torch.Size([1, 256, 12, 12])
MaxPool2d Output shape:     torch.Size([1, 256, 5, 5])
Flatten Output shape:     torch.Size([1, 6400])
Linear Output shape:     torch.Size([1, 4096])
ReLU Output shape:     torch.Size([1, 4096])
Dropout Output shape:     torch.Size([1, 4096])
Linear Output shape:     torch.Size([1, 4096])
ReLU Output shape:     torch.Size([1, 4096])
Dropout Output shape:     torch.Size([1, 4096])
Linear Output shape:     torch.Size([1, 10])
training on cuda:0
<Figure size 350x250 with 1 Axes>*n
loss 0.327, train acc 0.879, test acc 0.883
1447.3 examples/sec on cuda:0

进程已结束,退出代码0