个人主页:C++忠实粉丝
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C++忠实粉丝 原创BFS解决最短路问题(4)_为高尔夫比赛砍树
收录于专栏【经典算法练习】
本专栏旨在分享学习算法的一点学习笔记,欢迎大家在评论区交流讨论💌
目录
1. 题目链接
2. 题目描述
3. 解法
算法思路:
代码展示:
4. 算法总结
1. 题目链接
OJ链接 : 为高尔夫比赛砍树
2. 题目描述
你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 m x n 的矩阵表示, 在这个矩阵中:
0表示障碍,无法触碰1表示地面,可以行走比 1 大的数表示有树的单元格,可以行走,数值表示树的高度
每一步,你都可以向上、下、左、右四个方向之一移动一个单位,如果你站的地方有一棵树,那么你可以决定是否要砍倒它。
你需要按照树的高度从低向高砍掉所有的树,每砍过一颗树,该单元格的值变为 1(即变为地面)。
你将从 (0, 0) 点开始工作,返回你砍完所有树需要走的最小步数。 如果你无法砍完所有的树,返回 -1 。
可以保证的是,没有两棵树的高度是相同的,并且你至少需要砍倒一棵树。
示例 1:
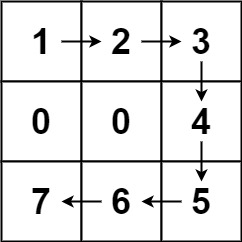
输入:forest = [[1,2,3],[0,0,4],[7,6,5]] 输出:6 解释:沿着上面的路径,你可以用 6 步,按从最矮到最高的顺序砍掉这些树。
示例 2:
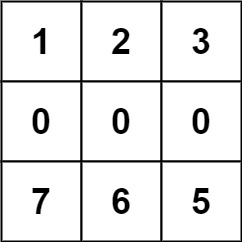
输入:forest = [[1,2,3],[0,0,0],[7,6,5]] 输出:-1 解释:由于中间一行被障碍阻塞,无法访问最下面一行中的树。
示例 3:
输入:forest = [[2,3,4],[0,0,5],[8,7,6]] 输出:6 解释:可以按与示例 1 相同的路径来砍掉所有的树。 (0,0) 位置的树,可以直接砍去,不用算步数。
提示:
m == forest.lengthn == forest[i].length1 <= m, n <= 500 <= forest[i][j] <= 109
3. 解法
算法思路:
1. 先找出砍树的顺序
2. 然后按照砍树的顺序, 一个一个的用bfs求出最短路即可.
1. 准备阶段
数据结构的准备:首先定义 m 和 n 来存储森林的行数和列数,使用 vector<pair<int, int>> 来保存所有需要砍伐的树的位置。
找到树木的位置:遍历整个森林,将所有树木(高度大于1的元素)的位置存储到 trees 向量中。
2. 排序
按照高度排序:对 trees 向量进行排序,使得树木按照高度升序排列。使用 std::sort 和一个自定义的比较函数,根据森林中树的高度来排序。
3. 砍树过程
初始化砍树的起始位置:起始位置为(0, 0),即森林的左上角。
循环砍伐树木:对于每棵树,调用 bfs 函数来计算从当前的位置到目标树的位置的最短路径。
如果路径不存在(返回 - 1),则直接返回 - 1。
如果路径存在,将步数累加到结果 ret 中,并更新当前的位置。
4. BFS搜索
BFS算法:在 bfs 函数中实现宽度优先搜索(BFS)来寻找从当前树的位置到目标树的位置的最短路径。
初始化:使用一个队列存储当前的搜索状态,使用 memset 清空访问记录 vis。
搜索过程:
进行层次遍历,逐步向四个方向扩展(上下左右),检查每一个可移动的点。
如果遇到目标树的位置,直接返回当前的步数。
如果队列为空且未找到目标,则返回 - 1。
代码展示:
class Solution {
int m, n;
public:
int cutOffTree(vector<vector<int>>& forest)
{
m = forest.size(), n = forest[0].size();
//1. 准备工作, 找出砍树的顺序
vector<pair<int, int>> trees;
for(int i = 0; i < m; i++)
for(int j = 0; j < n; j++)
if(forest[i][j] > 1) trees.push_back({i, j});
sort(trees.begin(), trees.end(), [&](const pair<int, int>& p1, const pair<int, int>& p2)
{
return forest[p1.first][p1.second] < forest[p2.first][p2.second];
});
//2. 按照顺序砍树
int bx = 0, by = 0;
int ret = 0;
for(auto& [a, b] : trees)
{
int step = bfs(forest, bx, by, a, b);
if(step == -1) return -1;
ret += step;
bx = a, by = b;
}
return ret;
}
bool vis[51][51];
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
int bfs(vector<vector<int>>& forest, int bx, int by, int ex, int ey)
{
if(bx == ex && by == ey) return 0;
queue<pair<int, int>> q;
memset(vis, 0, sizeof vis);
q.push({bx, by});
vis[bx][by] = true;
int step = 0;
while(q.size())
{
step++;
int sz = q.size();
while(sz--)
{
auto [a, b] = q.front();
q.pop();
for(int i = 0; i < 4; i++)
{
int x = a + dx[i], y = b + dy[i];
if(x >= 0 && x < m && y >= 0 && y < n && forest[x][y] && !vis[x][y])
{
if(x == ex && y == ey) return step;
q.push({x, y});
vis[x][y] = true;
}
}
}
}
return -1;
}
};
4. 算法总结
时间复杂度
遍历森林的复杂度为 O(m * n),而排序树木的复杂度为 O(k log k)(k为树的数量)。
BFS搜索的最坏情况复杂度为 O(m * n),因为每个位置最多被访问一次。
整体复杂度为 O(m * n + k log k)。
空间复杂度
使用了 O(m * n) 的空间来存储访问标记和队列,整体空间复杂度也是 O(m * n)。
总结
该算法通过将树木按高度排序,并使用 BFS 逐步计算每棵树之间的最短路径,从而确保在每一步都能按照要求的顺序砍伐树木。BFS 保证了路径的最短性,而排序确保了树木被砍伐的顺序正确。