引言
在海量数据的存储与检索中,如何在保持快速检索的同时,降低内存占用是个巨大的挑战。有没有一种既能快速检索又能节省内存的方案?布隆过滤器(Bloom Filter)就是这样一种数据结构。
布隆过滤器的基本原理
如果我们要判断某个元素是否在集合中,最直接的方式是保存集合中所有元素,然后通过遍历集合来查找。但是,当集合中的数据量变得非常大时,像数组、链表、哈希表等传统数据结构不仅需要大量存储空间,查找效率也会随之下降。
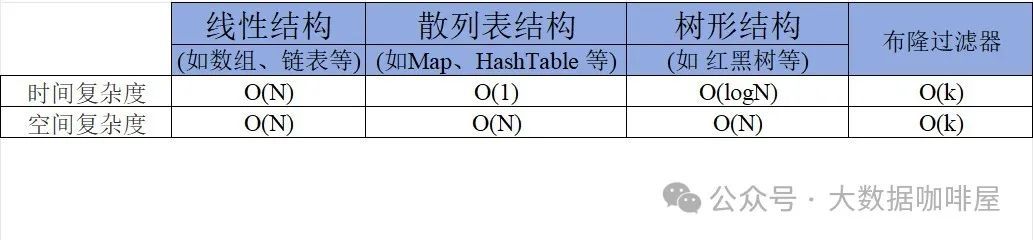
注意到对散列表来说,查找的复杂度非常低。
当往数组或列表中插入新数据时,将不会根据插入的值来确定其索引值。这意味着新插入的索引值与数据值之间没有直接关系。
哈希表可以通过对 “值” 进行哈希处理来获得该值对应的索引值,然后把该值存放到对应的索引位置。这意味着索引值是由插入项的值所确定的,当你需要判断列表中是否存在该值时,只需要对值进行哈希处理并在相应的索引位置进行搜索即可,这时的搜索速度是非常快的[1]。
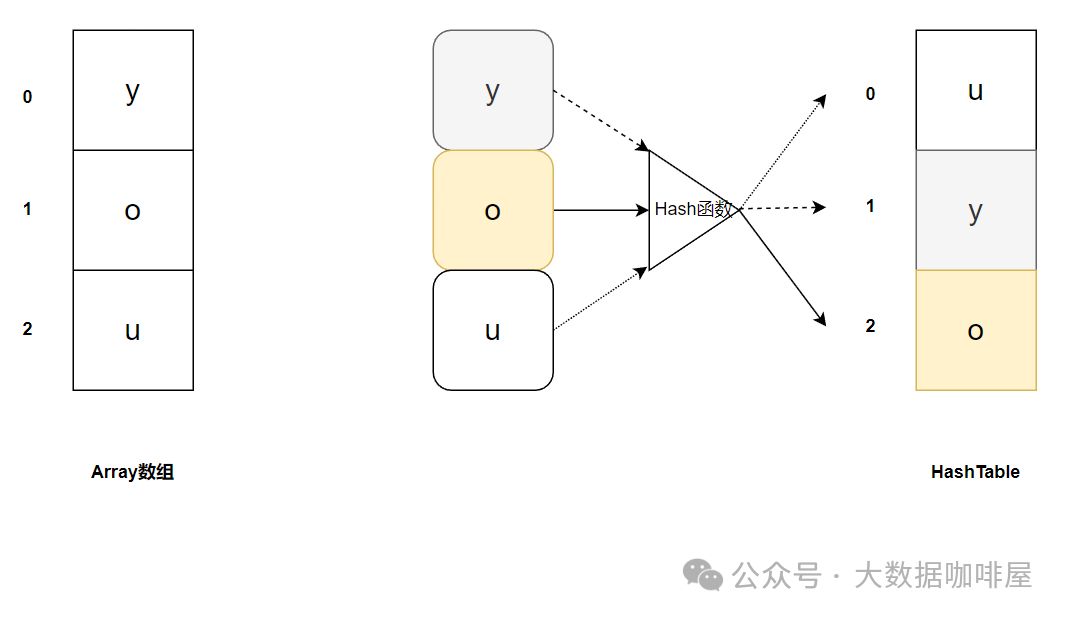
然而随着数据量的增加,哈希表所需的内存也急剧增加。
举例来说,假设有 10 亿条网址数据,每条网址占 64 字节,使用哈希表大约需要 64GB 内存,甚至更多。
在这种场景下,我们需要一种更为精简的结构来替代哈希表。
布隆过滤器就是这样一种节省空间且检索速度快的数据结构。它可以在不完全存储数据的情况下,通过少量空间来判断某个元素是否可能存在于集合中。
布隆过滤器(Bloom Filter)本质上是一个长度为 m 的位数组,最初所有的值均设置为 0(此处以m=10为例)。
当需要将某个元素加入布隆过滤器时,使用 K 个不同的哈希函数(此处以k=3为例)将该元素映射到数组的 K 个位置,并将对应的位设为 1。

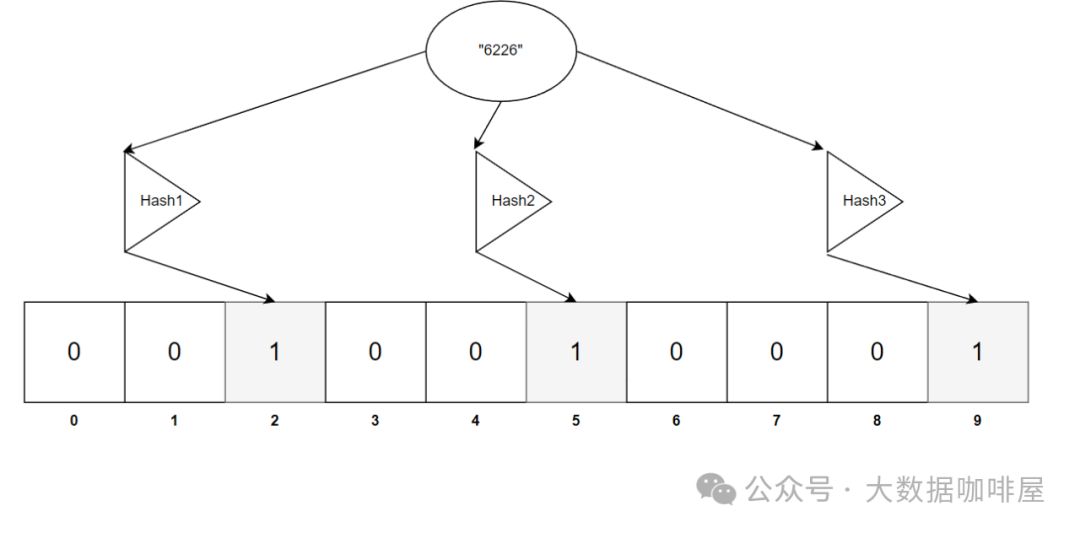
现在我们要将字符串 "6226" 存入布隆过滤器。经过 3 个哈希函数处理后,分别得到索引值 2、5、9,这些位置上的值将被设置为 1。
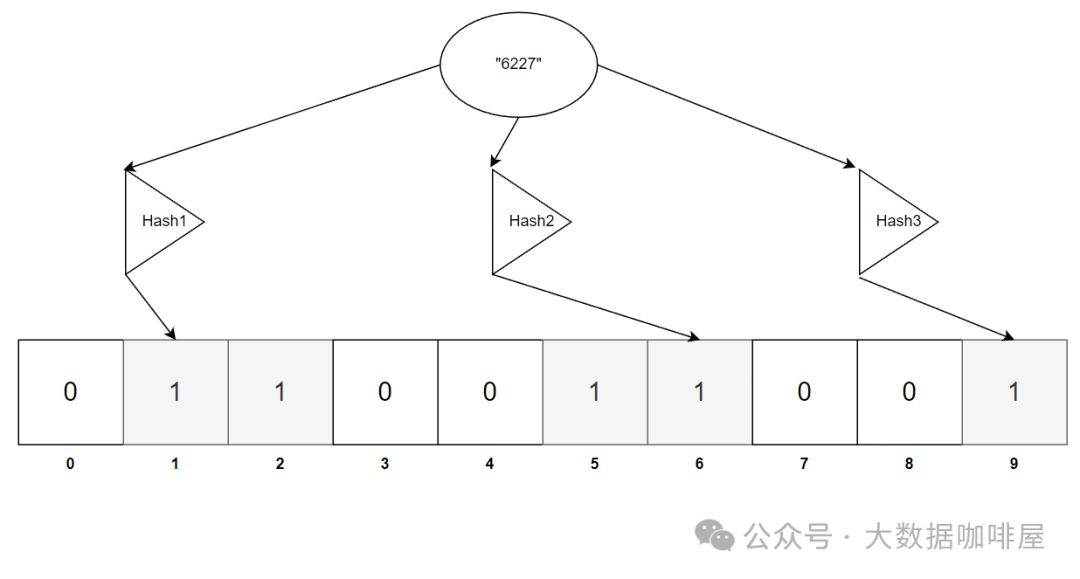
接着,我们再存入字符串 "6227"。哈希函数处理后,索引值为 1、6、9,这些位置上的值同样会被设置为 1。
这个过程重复多次将数据都放进去。
当查询一个数据是否存在时,算出经过三个hash函数转换并对10取模后的索引值。
看看这些三个位置上的数字是不是都是1就知道集合中有没有它了:如果这些点有任何一个0,则被检元素一定不存在;如果都是1,则被检元素很可能在[2]。
布隆过滤器可能出现”存在此元素“的误报现象,但是不会出现”不存在“的漏报现象。
误报现象是因为可能有多个元素经过处理后的索引值相同,导致该位置为 1, 那么一个不存在的元素也可能会被误判为存在。
对于要将n个数据放进一个长度为m的场景,为了尽量降低误报率,数学上有公式计算此场景下最优的哈希函数K的数量。
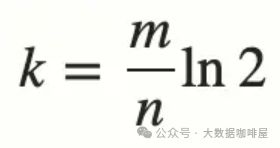
布隆过滤器在HBase中的应用
HBase 是大数据领域中常用的分布式数据库系统,能够高效存储和查询数十亿条数据。
它通过分块存储,将表的数据按顺序分为若干数据块,每块内的多个元素都算出一个布隆过滤器串。
通过预先对每个数据块建立一个布隆过滤器,来快速判断某个数据块是否可能包含该数据。如果布隆过滤器判断该数据块不可能包含目标数据,则可以跳过这个数据块,极大减少需要检索的数据块数量,从而加快查询速度。
假设一个数据块大小为 64KB,平均每个 rowkey 占 1KB。在使用 3 个哈希函数的情况下,按照上面的公式布隆过滤器需要的空间大约是80byte。
正是由于布隆过滤器只需占用极小的空间,便可给出“可能存在”和“肯定不存在”的存在性判断,因此可以提前过滤掉很多不必要的数据块。HBase 中的 Get 操作就是依赖于布隆过滤器的快速过滤机制,能够在大规模数据环境下显著提升查询速度[3]。
总结
布隆过滤器作为一种高效、低成本的空间优化方案,凭借其独特的“以小博大”能力,在大数据存储与查询场景中占据了重要地位。通过它的应用,HBase 可以在海量数据中迅速筛选出可能包含目标数据的块,大大提升查询效率。虽然布隆过滤器存在误报风险,但它从不漏报的特性,使其成为实际场景中不可或缺的工具。
在数据量持续增长的今天,布隆过滤器无疑是优化大数据存储与检索的利器,值得每个开发者深入理解并加以应用。
参考
1. 布隆过滤器:你值得拥有的开发利器 https://segmentfault.com/a/1190000021136424
2. 布隆过滤器 https://zh.wikipedia.org/wiki/%E5%B8%83%E9%9A%86%E8%BF%87%E6%BB%A4%E5%99%A8
3. HBase原理与实践 (数据库技术丛书)_胡争、范欣欣 P119-P120 & P234-P241